Теорема Лагранжа и следствия из нее

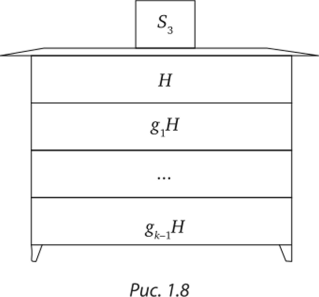
Рассмотрим разложение конечной группы G на левые смежные классы по подгруппе Я (рис. 1.8): G = Н и ?, Я u g₂H и … и g_k_]H.

Поскольку, как мы доказали, в каждом смежном классе столько же элементов, сколько их в подгруппе Я, то | G - Я -к. Этот же результат мы получим, рассматривая разложение данной группы на правые смежные классы по той же подгруппе. Таким образом, доказана следующая теорема.

Теорема 1.7 (Лагранжа). Порядок конечной группы равен произведению порядка подгруппы на число левых (правых) смежных классов по этой подгруппе.

Из теоремы Лагранжа вытекает, что число левых смежных классов конечной группы G по подгруппе Я равно числу правых смежных классов по этой подгруппе. Докажем, что это верно в любой группе.

Теорема 1.8. В любой группе G число (мощность множества) левых смежных классов по подгруппе Н равно числу (мощности множества) правых смежных классов по этой подгруппе.

Доказательство. Сопоставляя всякому левому смежному классу gH правый смежный класс Hg^-1, мы получаем взаимно однозначное отображение множества всех левых смежных классов по подгруппе Я на множество всех правых смежных классов по этой подгруппе, что и доказывает теорему.

Доказанное свойство приводит к следующему определению.

Определение 1.11. Индексом в группе G подгруппы Я называется количество (мощность множества) левых или правых смежных классов по этой подгруппе.

Индекс обозначается |G: Я|.

С помощью введенного понятия теорему Лагранжа можно записать так: |G| = |Я| • |G: Я|. Читается: порядок конечной группы G равен произведению порядка подгруппы Я на ее индекс.

Следствие 1. Порядок подгруппы конечной группы является делителем порядка группы.

Заметим, что если | G |: т, то отсюда совсем не следует, что группа G содержит подгруппу порядка т. Например, группа четных подстановок четырех символов Д₄ имеет порядок 12, но, как легко видеть, она не содержит подгрупп порядка 6.

Следствие 2. Порядок элемента конечной группы является делителем порядка группы.

Доказательство. Пусть группа G конечна и а е G. По теореме 1.3 |(а)| = |а|, а по следствию 1 |G|: |(а)| = |а|.

Следствие 3. Группа простого порядка циклическая.

Доказательство. Пусть | G | -р, где р — простое число, и е Ф Д а е G. По следствию 2 порядок элемента а является делителем числа р, отличным от единицы. Следовательно, | а — р

и группа G исчерпывается всеми степенями элемента а. Другими словами, G = (а).

Следствие 4. Если | G | = п, то а^п = е для любого а е G. Доказательство. Пусть | а = т. По следствию 2пт. Пусть п = mq, q е Z, тогда а^п = а^тя = еч = е.