Анализ пяти раундов алгоритма шифрования Rijndael с помощью невозможных дифференциалов

Рассмотрим алгоритм шифрования Rijndael, состоящий из 4-х циклов. Если пара открытых текстов имеет различие только лишь в одном байте, то соответствующие им шифр-тексты нс могут иметь одинаковые значения в следующих комбинациях байтов: (1, 6, 11, 16), (2, 7, 12, 13), (3, 8, 9, 14) или (4, 5, 10, 15). Это происходит вследствие того, что перед преобразованием MixColumn в первом раунде различие имеется только в одном байте, после преобразования — во всем столбце, а после преобразования MixColumn второго раунда — во всех 16 байтах. С другой стороны, если шифр-тексты имеют одинаковые значения в одной из запрещенных комбинаций байтов, то после преобразования MixColumn третьего раунда данные имеют одинановые значения в одном из столбцов, а это значит, что и до преобразования MixColumn третьего раунда данные также имеют одинаковые значения в этом столбце. Следовательно, после преобразования MixColumn второго раунда в данных осталось четыре байта, равных между собой. Это противоречит тому, что мы выяснили ранее: после преобразования MixColumn данные должны иметь различия во всех байтах. Заметим, что вероятность возникновения такого противоречия при рассмотрении случайной пары текстов равна 2"° [26].

Таким образом, анализ пяти раундов алгоритма шифрования Rijndacl основан на исключении неправильных подключей первого раунда, при использовании которых в последних четырех раундах появляется значение невозможной разности. Нам необходимо рассмотреть такие пары текстов, которые на входе второго раунда шифрования будут иметь различие только в первом байте. Это возможно в том случае, когда на вход алгоритма шифрования поступает пара текстов, имеющая различие в первом, шестом, одиннадцатом и шестнадцатом байтах (рис. 100). На рис. 103 серым цветом обозначены байты, в которых тексты не имеют сходства.

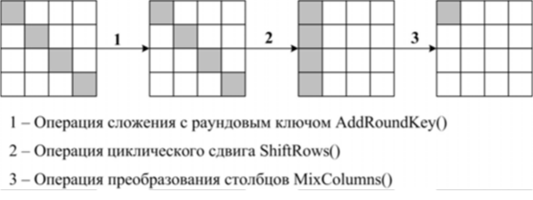
Рис. 103. Анализ алгоритма шифрования Rijndael.

Зная это, можно провести анализ данного алгоритма шифрования по следующей схеме.

• 1. Выбрать 2^6-' пар открытых текстов, таких, что разность в первом, шестом, одиннадцатом и шестнадцатом байтах у них не будет равна нулю.
• 2. Зашифровать их на одном и том же секретном ключе.
• 3. Выбрать те пары текстов, у которых разность шифртекстов имеет ненулевые значения в одной из невозможных комбинаций байтов. Таких пар будет примерно 2^fu * 2'³⁰ ~ 2³'.
• 4. Для каждой такой пары открытых текстов (Р, Р*) выполнить следующие действия:
  • а) предположить значение первого, шестого, одиннадцатого и шестнадцатого байтов первого подключа К⁰;
  • б) вычислить, чему будут равны первый, пятый, девятый и тринадцатый байты выхода первого раунда для шифр-текстов Р и Р*, зашифровав их с помощью выбранных байтов подключа К⁰;
  • в) если разность первых вычисленных байтов отлична от нуля, а разность остальных вычисленных байтов равна нулю, то байты подключа К⁰ выбраны неверно;
  • г) продолжать выполнять действия пп. а, б и в до тех пор, пока не будет найдено верное значение байтов первого подключа.

Остальные байты первого подключа могут быть найдены с использованием аналогичной схемы, однако рассматривать в этом случае надо не первый столбец второго раунда, а все остальные.

Обе вышеприведенные атаки на алгоритм Rijndacl легко могут быть реализованы с использованием распределенных многопроцессорных вычислений. Особенно это актуально для метода анализа на основе невозможных дифференциалов, где для анализа необходимо обработать довольно большой массив данных. Более подробную информацию об анализе алгоритма AES можно найти в работах [7, 9, 26].