Линейный криптоанализ. 
Криптографическая защита информации: симметричное шифрование

Метод линейного криптоанализа впервые был предложен в начале 90-х гг. XX в. японским ученым М. Матсуи (Matsui). В своей работе [18] он показал, как можно осуществить атаку на алгоритм шифрования DES, сократив сложность анализа до 2⁴⁷.

Существенным недостатком метода стала необходимость иметь в наличии большой объем данных, зашифрованных на одном и том же секретном ключе, что делало метод малопригодным для практического применения к вскрытию шифра. Однако, если предположить, что к аналитику в руки попал шифрованный текст, содержащий важные сведения, а также некий черный ящик (устройство или программа), который позволяет выполнить любое число текстов, зашифрованных с помощью известного алгоритма шифрования на секретном ключе, не раскрывая при этом самого ключа, то применение метода линейного криптоанализа становится вполне реальным. Многие алгоритмы шифрования, известные на момент опубликования работы [18], впоследствии были проверены на устойчивость к этому методу и не все из них оказались достаточно стойкими и, как следствие, потребовали доработки.

Знание механизмов работы метода линейного криптоанализа позволяет криптографам еще на этапе проектирования крптоалгоритмов обеспечить стойкость шифров. Вот почему так важно уметь применять известные методы криптоанализа на практике.

Итак, рассмотрим основные понятия, связанные с методом линейного криптоанализа. Любой алгоритм шифрования в самом общем виде можно представить как некоторую функцию Е, зависящую от входного сообщения X, секретного ключа К и возвращающую шифрованное сообщение Y:

Зная само преобразование Е и входное сообщение X, нельзя однозначно сказать, каким будет выходное сообщение Y. В данном случае нелинейность функции (13) зависит от внутренних механизмов преобразования Е и секретного ключа К. М. Матсуи показал, что существует возможность представить функцию шифрования (13) в виде системы уравнений, которые выполняются с некоторой вероятностью р. При этом для успешного проведения анализа вероятность уравнений р должна быть как можно дальше удалена от значения 0,5 (т. е. приближаться либо к нулю либо к единице). Так как уравнения, получаемые в ходе анализа криптоалгоритма, являются вероятностными, их стали называть линейными статистическими аналогами.

Определение. Линейным статистическим аналогом нелинейной функции шифрования (13) называется величина Q, равная сумме по модулю 2 скалярных произведений входного вектора X, выходного вектора Y и вектора секретного ключа К соответственно с двоичными векторами а, р и у, имеющими хотя бы одну координату, равную единице:

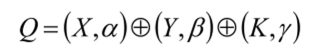
в том случае, если вероятность того, что Q=0 отлична от 0,5 (P (Q=0)#), 5).

В отличие от дифференциального криптоанализа, в котором большое значение вероятности гарантирует успех атаки, в линейном криптоанализе успех анализа может быть обеспечен как уравнениями с очень большой вероятностью, так и уравнениями с очень маленькой вероятностью. Для того чтобы понять, какое из возможных уравнений лучше всего использовать для анализа, используют понятие отклонения.

Определение. Отклонением линейного статистического аналога называют величину ту = 11 — 2р|, где р — вероятность, с которой выполняется линейный аналог.

Отклонение определяет эффективность линейного статистического аналога. Чем отклонение больше, тем выше вероятность успешного проведения анализа. Фактически отклонение показывает, насколько вероятность статистического аналога отдалена от значения р = 0,5.

Для успешного применения метода линейного криптоанализа необходимо решить следующие задачи:

• 1. Найти максимально эффективные (или близкие к ним) статистические линейные аналоги. При нахождении аналогов обратить внимание на то, что в них должно быть задействовано как можно больше битов искомого секретного ключа К.
• 2. Получить статистические данные: необходимый объем пар текстов (открытый — закрытый текст), зашифрованных с помощью анализируемого алгоритма на одном и том же секретном ключе.
• 3. Определить ключ (или некоторые биты ключа) путем анализа статистических данных с помощью линейных аналогов.

Первый шаг анализа заключается в нахождении эффективных статистических аналогов. Для алгоритмов шифрования, в которых все блоки заранее известны, этот шаг можно выполнить единожды, основываясь на анализе линейных свойств всех криптографических элементов шифра. В результате анализа должна быть получена система уравнений, выполняющихся с некоторыми вероятностями. Левая часть уравнений должна содержать в себе сумму битов входного и выходного сообщения, правая часть уравнения — биты секретного ключа. Система уравнений должна быть определенной, т. е. содержать все биты исходного секретного ключа. Данный этап не является вычислительно сложным, однако требует больших знаний, логики работы и внимательности. Он может быть автоматизирован. Однако при этом необходимо помнить, что для каждого определенного алгоритма шифрования система линейных аналогов строится всего один раз и в дальнейшем может быть использована для нахождения разных секретных ключей шифрования, которые используются для шифрования данных с помощью анализируемого шифра.

Если первый шаг анализа является чисто теоретическим и полностью зависит от структуры алгоритма, то второй шаг является исключительно практической частью, которая заключается в анализе известных пар открытый — закрытый текст с помощью полученной ранее системы статистических аналогов. Для этого используется следующий алгоритм.

Алгоритм. Пусть N — число всех открытых текстов и Т — число открытых текстов, для которых левая часть линейного статистического аналога равна 0. Рассмотрим два случая.

• 1. Если T>N/2, то в этом случае число открытых текстов, для которых левая часть аналога равна нулю, больше половины, т. е. в большинстве случаев в левой части аналога появляется значение, равное нулю:
  • а) если вероятность этого линейного статистического аналога р >½, это говорит о том, что в большинстве случаев правая и левая части аналога равны, а значит, левая часть аналога, содержащая биты ключа, равна 0;
  • б) если вероятность этого линейного статистического аналога р < ½, это говорит о том, что в большинстве случаев правая и левая части аналога не равны, а значит, левая часть аналога, содержащая биты ключа, равна 1.
• 2. Если T
  • а) если вероятность этого линейного статистического аналога р >½, это говорит о том, что в большинстве случаев правая и левая части аналога равны, а значит, левая часть аналога, содержащая биты ключа, равна 1;
  • б) если вероятность этого линейного статистического аналога р < ½, это говорит о том, что в большинстве случаев правая и левая части аналога не равны, а значит, левая часть аналога, содержащая биты ключа, равна 0.

Пользуясь приведенным выше алгоритмом, можем обобщить вышесказанное для уравнения X (c)Y = К.

Если T>N/2, то.

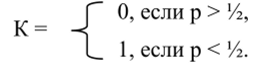
Если T.

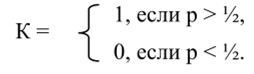
Успех алгоритма возрастает с ростом N и Д = |1 — 2р|.

Данный алгоритм будет иметь успех при анализе большого числа текстов N. Следовательно, второй шаг анализа является вычислительно сложным. Поэтому для ускорения времени анализа можно и нужно использовать параллельные вычисления.

В результате работы вышеприведенного алгоритма будет получена определенная (а возможно, и переопределенная) система уравнений, отражающая взаимосвязь битов ключа. Третий шаг анализа заключается в решении данной системы, например, методом Гаусса, что позволит получить значения битов секретного ключа шифрования.

Более подробно о линейном криптоанализе различных блочных алгоритмов шифрования можно прочитать в работе.

[9].