Теорема Калладина—Друккера. 
Расчеты на ползучесть элементов машиностроительных конструкций

В некоторых случаях приближенные решения задач установившейся ползучести равномерно нагретых тел можно получить с помощью теоремы Калладина — Друккера [35, 36]. Согласно этой теореме в случае степенной зависимости скорости деформации или деформации ползучести от напряжения поверхности постоянной нормированной работы диссипации в пространстве сил для определенного момента времени вложены друг в друга й заключены между поверхностями для п — 1 (упругое тело) и п = оо (идеально пластическое тело).

Поскольку, как уже указывалось выше, решения задач установившейся ползучести совпадают с решениями чистоиластических задач по теории малых упругопластических деформаций, отношение деформации ползучести к функции Q может быть представлено в виде.

где согласно формуле (4.150) и учитывая то, что в условиях ползучести изменение объема равно нулю (К = оо), имеем.

Используем теперь степенную зависимость интенсивности деформации ползучести от интенсивности напряжений (3.13). Тогда выражение (4.156) принимает вид.

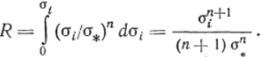
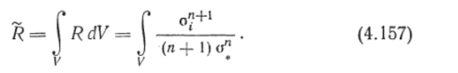
Дополнительная работа всего тела Введем понятие работы диссипации:

L = о it], (4.158).

В случае степенной зависимости интенсивности деформаций ползучести от интенсивности напряжений (3.13) соотношение (4.158) принимает вид L = о" ⁺¹/а".

Работа диссипации всего тела.

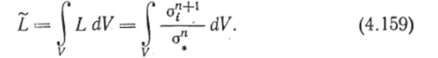
Переходя к доказательству теоремы, представим себе два одинаковых, одинаковым образом нагруженных тела с различными показателями степени: п_х — для первого тела и п₂ — для второго, причем примем п₂ > п_г. Обозначим напряжения, возникающие в первом теле, через (а, у)" а во втором — через (о_|;)₂. Выберем в качестве стандартных такие системы нагрузок X_vjl и X_vj2t

приложенных к первому и второму телам соответственно, при которых безразмерные работы диссипации всего тела на единицу его объема равны единице, т. е.

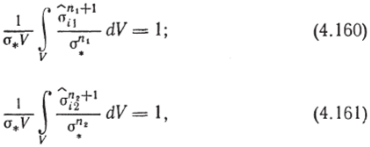
где a, i и а₍₂ — интенсивности напряжений соответственно в первом и втором телах при нагрузках X_vil и X_vi2,. Обозначим напряжения при этих нагрузках (o,_;)j и (cr,_;-)_s соответственно. Заметим, что согласно теореме о простом нагружении [50] напряжения.

(o_{i (})₂X_VJ1/X_VJг" удовлетворяют дифференциальным уравнениям равновесия и граничным условиям, соответствующим силам X_vjt. Поэтому можно считать, что они определяют статически возможное для первого тела состояние, и по теореме о минимуме дополнительной работы для всего тела 150], используя соотношение (4.157), имеем.

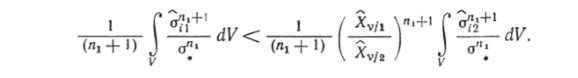
Разделив обе части равенства на ст"Р и используя соотношение (4.160), получим.

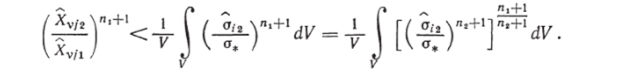
Усилим последнее неравенство, используя теорему Гельдера (84), согласно которой.

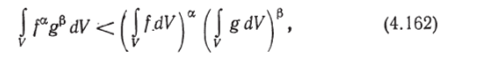
при условии, что а > 0, р > 0, afр = 1.

Полагая в неравенстве (4.162)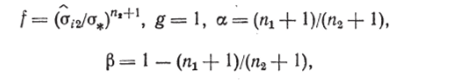

получим.

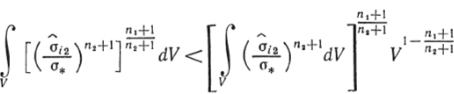
и, следовательно.

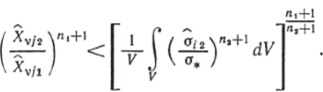
На основании равенства (4.161) X_vji < X_vjl, откуда следует, что в пространстве сил поверхность постоянной нормированной работы диссипации для п₂ > n_L вложена в соответствующую поверхность для п₂. Следовательно, все такие поверхности расположены между соответствующими поверхностями для п = 1 (упругое тело) и п — оо (идеально пластическое тело).

Рассмотрим применение доказанной теоремы для решения задачи установившейся ползучести растянутого и изогнутого стержня прямоугольного поперечного сечения (рис. 4.37). Предварительно наметим точное решение. Зависимость напряжения а от величины ё устанавливаем из формулы (3.13):

Для указанного нагружения поперечное сечение стержня остается плоским и, следовательно, е = е₀ —к.у и.

aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">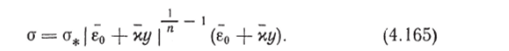

где ё₀ = е₀/Й; х = х/й, а е₀ — линейная деформация оси стержня, х — кривизна ее. Подставим соотношение (4.164) в формулу (4.163):

Нормальная сила и изгибающий момент связаны с напряжением соответственно соотношениями N = J a dF М = J csydF.

F F

Рис. 4.37. Растянутый и изогнутый стержень прямоугольного поперечного сечения.

Используя выражение (4.165) и учитывая, что dF = bdy, имеем.

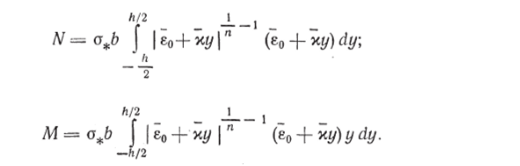
Очевидно, что вычисление этих интегралов позволяет установить зависимость нормальной силы и изгибающего момента от деформации и кривизны оси стержня. Однако подсчет последних величин по нормальной силе и изгибающему моменту связан со значительными трудностями, так как разрешение полученных уравнений относительно ё₀ и х невозможно. Для преодоления этих трудностей используем теорему Калладина —Друккера.

Подберем аппроксимирующую функцию Ф для дополнительной работы всего тела R = R (Ф), так, чтобы при /V = О Ф = = М.

На основании теоремы Кастилиано [501.

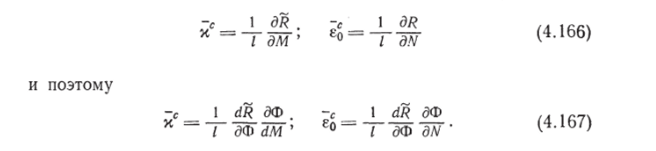
При отсутствии нормальной силы N = 0 (Ф = Л!) согласно первой формуле (4.167) и формулам (4.16), (4.18) и (4.19) имеем.

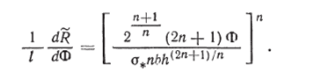
Проинтегрировав это уравнение с учетом того, что при Ф = 0 R = 0, получим.

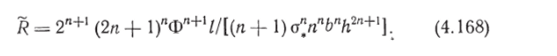
Для выбора функции Ф разберем вначале упругое состояние Рис. 4.39. Графики уравнений (4.69) и (4.71)

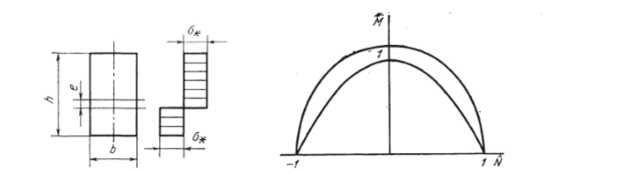
Рис. 4.38. Эпюра напряжений в предельном состоянии растянутого и изогнутого стержня.

стержня (п = 1). В этом случае напряжения определяются по формуле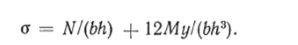

Составим условие нормирования:

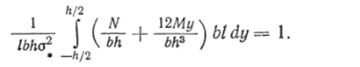
Вычисляя интеграл после преобразований, получим.

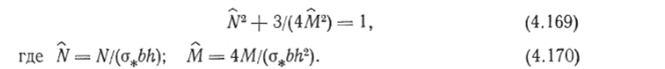
Разберем теперь предельное состояние, в котором напряжения в растянутой и сжатой областях распределены равномерно и одинаковы по абсолютной величине (л = оо). Эпюра напряжений в этом случае представлена на рис. 4.38. Обозначим смещение нейтральной линии через е и составим выражение для нормальной силы и изгибающего момента:

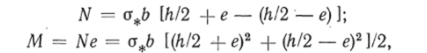
откуда после исключения величины е получаем.

Таким образом, в координатах N, М график условия нормирования работы диссипации является эллипсом (4.169), а график условия предельного состояния — параболой (4.171). Они изображены на рис. 4.39. Все кривые постоянной нормированной мощности диссипации пройдут через точки на оси абсцисс с координатой ±1. Для того чтобы найти пересечение с осью ординат кривой постоянной нормированной работы диссипации, соответствующей определенному показателю степени п, подчиним работу диссипаВ случае чистого изгиба стержня прямоугольного поперечного сечения нормальные напряжения в поперечном сечении определяются по формулам (4.17). Подставив соотношения (4.17) в выражение (4.172) и использовав формулы (4.18) и (4.19), после преобразований получим.

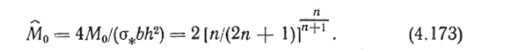
Из этого выражения следует, что при п = 1 М₀ = 2/|/3, а при.

п = оо М" = 1, что согласуется с уравнениями (4.169) и (4.171). Следовательно, все кривые постоянной нормированной работы диссипации проходят через точку, ордината которой на оси ординат изменяется от 1 до 2/</3, и согласно теореме Калладина — Друккера расположены между эллипсом (4.169) и параболой (4.171), причем с возрастанием показателя степени п они оказываются вложенными одна в другую. Примем, что эти кривые являются эллипсами, уравнение которых.

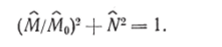
Исходя из полученного результата, учитывая, что при N = 0 Ф = М, и используя вторую формулу (4.170), заключаем, что.

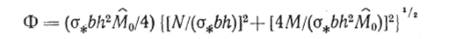
и, следовательно, согласно формуле (4.168).

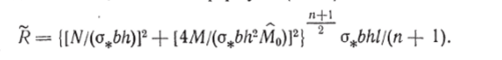
По формулам (4.166) получаем.

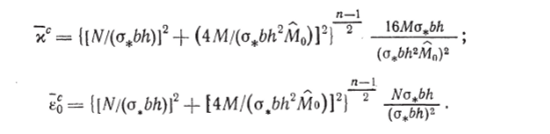
ции для чистого изгиба (JV = 0) условию нормирования;

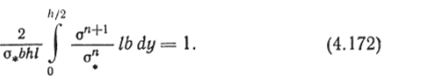
Легко убедиться в том, что в частных случаях чистого изгиба и растяжения последние формулы дают точные решения.