Многоканальная СМО с неограниченной очередью

Рассмотрим многоканальную СМО с ожиданием и неограниченной длиной очереди, на которую поступает поток заявок с интенсивностью А, и которая имеет интенсивность обслуживания каждого канала р. Размеченный граф состояний многоканальной СМО с неограниченной очередью представлен на рис. 5.19. Он имеет бесконечное число состояний:

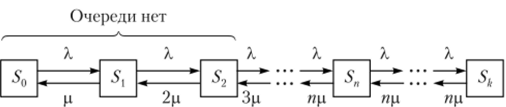
Рис. 5.19.

So — вес каналы свободны, к = 0;

— занят один канал, остальные свободны, к = 1;

S2 — заняты два канала, остальные свободны, к = 2;

S_n — заняты все п каналов, к = п, очереди нет;

• 5"+1 — заняты все п каналов, одна заявка в очереди, k = п + 1;
• 5_w+r — заняты все п каналов, г заявок в очереди, к = п + г.

Вероятности состояний получим из формул для многоканальной СМО с ограниченной очередью при переходе к пределу при т —³? Следует заметить, что сумма геометрической прогрессии в выражении для ро расходится при уровне загрузки р/п > 1, очередь будет бесконечно возрастать, а при р/п < 1 ряд сходится, что определяет установившийся стационарный режим работы СМО, для которого и определим выражения для предельных вероятностей состояний.

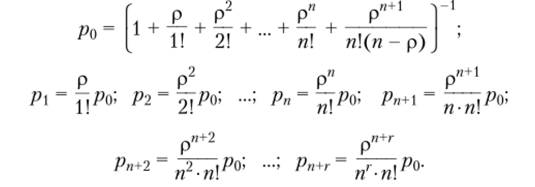
Поскольку отказа в обслуживании в таких системах не может быть, то характеристики пропускной способности равны.

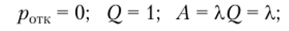
• среднее число заявок в очереди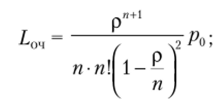

• среднее время ожидания в очереди.

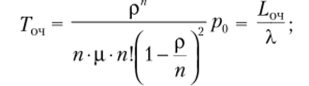
• среднее число заявок в СМО.

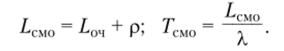
Вероятность того, что СМО находится в состоянии Sq, когда нет заявок и не занято пи одного канала, определяется выражением.

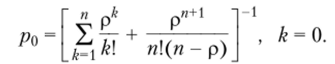
Эта вероятность определяет среднюю долю времени простоя канала обслуживания.

Вероятность занятости обслуживанием k заявок.

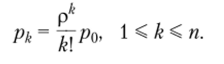
На этом основании можно определить вероятность, или долю времени, занятости всех каналов обслуживанием:

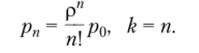
Если же все каналы уже заняты обслуживанием, то вероятность состояния определяется выражением.

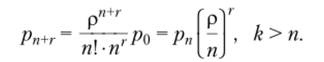
Вероятность оказаться в очереди равна вероятности застать все каналы уже занятыми обслуживанием:

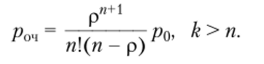
Среднее число заявок, находящихся в очереди и ожидающих обслуживания,.

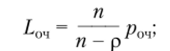
• среднее время ожидания заявки в очереди по формуле Литтла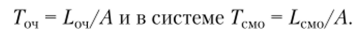

• среднее число занятых каналов обслуживанием.

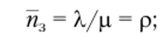
• среднее число свободных каналов.

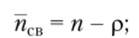
• коэффициент занятости каналов обслуживанием.

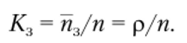
Важно заметить, что параметр р характеризует степень согласования входного потока, например покупателей в магазине, с интенсивностью потока обслуживания. Процесс обслуживания будет стабилен при р < п. Если же р > п, в системе будут возрастать средняя длина очереди и среднее время ожидания покупателями начала обслуживания и, следовательно, СМ О будет работать неустойчиво.

Рассмотрим применение моделей для анализа работы СМО с ожиданием на нескольких примерах.

Пример 5.25. В столовой к узлу расчета поступает пуассоновский поток посетителей с интенсивностью X = 120 человек в час. Средняя продолжительность обслуживания контролером-кассиром одного посетителя составляет T_Qб_с =1,0 мин. Определим оптимальное число контролеров-кассиров п₀, при котором общие издержки С, определяемые затратами, с одной стороны, на содержание контролеров-кассиров С_ио, а с другой — пребыванием посетителей в очереди С_ип, были бы минимальны.

На этом основании целевую функцию можно записать.

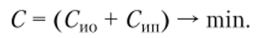
Издержки С_ио определяются числом каналов обслуживания п, величиной затрат, связанных с содержанием в системе одной обслуживающей единицы в течение одной единицы времени С* (руб/ч) и интенсивностью входного потока X.

Издержки потребления С_ип определяются величиной удельных потерь С_оч, связанных с пребыванием в очереди одного покупателя в течение единицы времени и средним временем ожидания в очереди Г_оч. Тогда целевую функцию затрат, связанную с пребыванием покупателей в системе в течение единицы времени, можно записать.

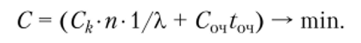
Для удобства проведения вычислений предположим, что С_оч/С* = 3/1, что позволит определить соотношение стоимостей обслуживания для разных вариантов организации системы. Для наглядности решения задачи построим график целевой функции.

С = f (n), но которому найдем минимум затрат, величина которого укажет на оптимальную численность контролсров-кассиров.

Следует заметить, что длина очереди — один из основных показателей эффективности СМО. Причем если длина очереди в системе может бесконечно возрастать, то рациональной организации системы нельзя получить. Только при условии р < п очередь может быть конечна, т. е. число заявок, поступающих в СМО за промежуток времени, равный средней длительности обслуживания Т₀(_ю меньше числа обслуживающих каналов. Это обусловлено вероятностным характером как потока заявок, так и временем их обслуживания. Поэтому о рациональности варианта организации СМО можно рассуждать лишь в том случае, если п > р. Поскольку из условия задачи следует, что интенсивность нагрузки р = Х/х = 2, то вычисления показателей системы следует начать с п = 3.

Сначала определяем долю времени простоя контролсров-кассиров в течение рабочего дня, т. е. при условии отсутствия покупателей.

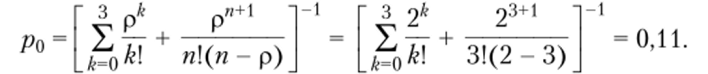
Следовательно, три контролера-кассира будут простаивать 11% времени от всей продолжительности рабочего дня. Результаты вычислений запишем в табл. 5.11.

Таблица 5.11

Вероятность застать всех контролеров-кассиров занятыми определяется по формуле Эрланга.

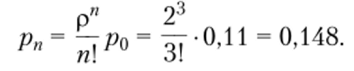
Вероятность оказаться в очереди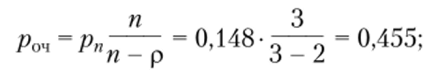

• среднее число покупателей, находящихся в очереди,.

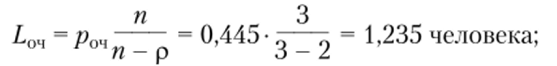
• среднее время ожидания покупателями в очереди начала обслуживания.

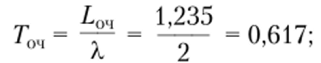
• относительная величина затрат для п = 3 и С_оч = ЗС* составляет.

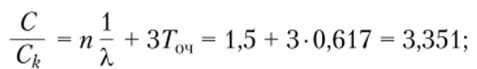
• среднее время пребывания посетителя в узле расчета.

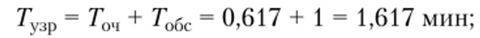
• среднее число занятых обслуживанием контролеров-кассиров.

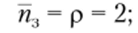
• среднее число свободных контролеров-кассиров.

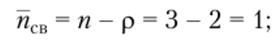
• коэффициент занятости контролеров-кассиров обслуживанием, т. е. нагрузка на одного контролера-кассира, или доля занятых обслуживанием каналов, составляет.

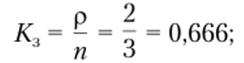
• среднее число покупателей в узле расчета.

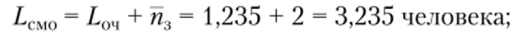
• абсолютная пропускная способность узла расчета в столовой.

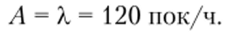
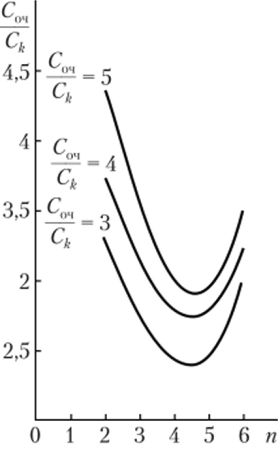
Рис. 5.20.

Затем проводим аналогичные вычисления по определению перечисленных показателей для других значений п = 4,5, 6, 7 и результаты запишем в табл. 5.11 и представим в виде рис. 5.20.

По данным таблицы следует, что оптимальное число контролеров-кассиров в узле расчета щ = А для соотношения С_оч: С = 3:1, при этом общие затраты будут минимальными.

Для целей расширения анализа проведены вычисления для разных вариантов соотношения С_оч: С* = 4, 5, которое, по данным таблицы, влияет на оптимальную численность контролеров-кассиров.

Пример 5.26. В расчетном узле магазина самообслуживания работают три кассы. Интенсивность входного потока составляет пять покупателей в минуту. Интенсивность обслуживания каждого контролера-кассира составляет два покупателя в минуту. Определим характеристики С МО и дадим оценку ее работы.

Решение

Определяем характеристики системы массового обслуживания:

• интенсивность нагрузки.

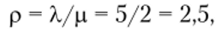
поскольку условие устойчивой работы р < п выполнено, 2,5 < 3, то можно определять предельные вероятности состояний;

• доля времени простоя узла расчета.

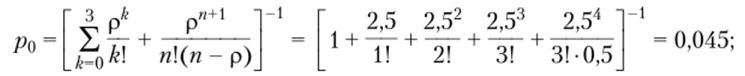
• вероятность того, что заявка окажется в очереди,.

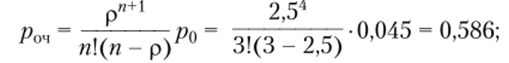
• средняя длина очереди.

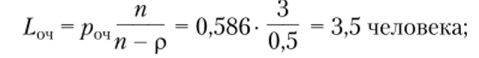
• среднее время пребывания в очереди.

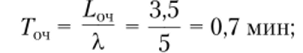
• среднее число покупателей в магазине.

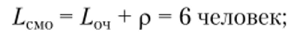
• среднее количество занятых каналов.

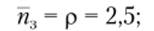
• коэффициент занятости каналов.

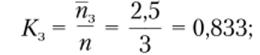
• среднее время пребывания заявки в магазине.

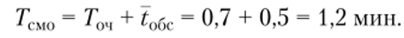
Доля времени простоя расчетного узла в магазине самообслуживания составляет всего 4,5% продолжительности рабочего дня, а вероятность оказаться в очереди велика — 58,6%, длина очереди небольшая — всего 3,5 покупателя, время ожидания в очереди — 0,7 мин, а коэффициент занятости каналов — 83,3%, поэтому система работает удовлетворительно. Следует иметь в виду, что при увеличении интенсивности входного потока X может нарушиться стационарный режим работы СМО, и при р > п очередь будет нарастать и система не будет справляться с обслуживанием.

Пример 5.27. В магазине самообслуживания установлены два кассовых аппарата. Интенсивность входного потока в будние дни в среднем составляет 1,3 покупателя/мин до обеда, 1,8 иокуиателя/мин — после обеда, а в субботу и воскресенье — в среднем 2,2 покупателя/мин. Среднее время обслуживания покупателя контролером-кассиром составляет 52 с. Проведем анализ работы системы массового обслуживания магазина.

Решение

Определяем характеристики СМ О отдельно для каждого варианта значения интенсивности входного потока:

• интенсивность нагрузки.

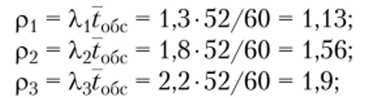
поскольку п = 2, то р > п и, следовательно, возможен стационарный режим работы, при котором доля времени простоя кассиров.

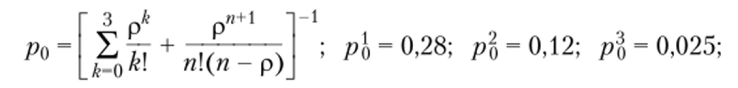
• вероятность оказаться в очереди.

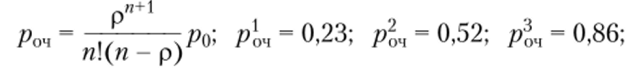
• среднее число покупателей в очереди.

• среднее число покупателей в магазине.

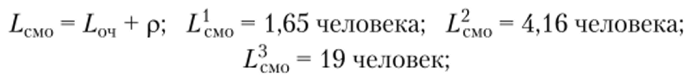
• среднее число занятых каналов.

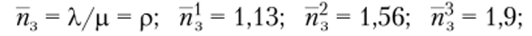
• среднее время пребывания заявки в очереди.

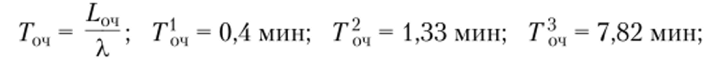
• среднее время пребывания заявки в магазине.

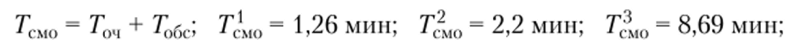
• коэффициент занятости каналов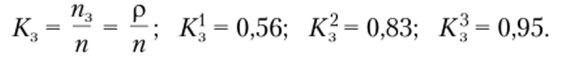

Интенсивность входного потока влияет на все характеристики СМО, доля времени простоя уменьшается до 2,5%, вероятность образования очереди увеличивается до 0,86, среднее число покупателей в очереди увеличивается до 17 человек, что уже недопустимо, поскольку потенциальные покупатели будут уходить к конкурентам, что в конечном счете приведет к уменьшению длины очереди и снижению экономических показателей, поэтому необходимо ориентироваться на покупателей и стремиться обслужить всех путем введения дополнительного кассового аппарата после обеда, в субботние и воскресные дни, ориентируясь на режим работы с длиной очереди в три покупателя.

Контрольные вопросы и задания.

• 1. Зачем нужны характеристики СМО?
• 2. Как пользоваться характеристиками СМО с отказами в коммерческой деятельности?
• 3. Как применять характеристики СМО с ожиданием в коммерческой деятельности?
• 4. Как аргументировать построение СМО с ограничением на длину очереди в коммерческой деятельности?
• 5. Каким образом можно оценить свою деятельность с помощью характеристик СМО?
• 6. Как можно провести оценку работы вашего руководителя на основе характеристик СМО?
• 7. Проведите оценку работы характеристиками СМО минимаркета, книжного киоска или любого другого торгового предприятия.
• 8. Проведите оценку согласованности взаимодействия студентов в группе с помощью характеристик СМО в процессе выполнения фрагментов учебного процесса: выполнения курсовых работ, подготовки и сдачи зачетов, экзаменов.
• 9. Дайте оценку взаимодействия членов вашей семьи утром характеристиками СМО.