Задачи с решениями

Задача 9.1^[1]. Исследователь считает, что уровень активности в теневой экономике Y зависит либо положительно от налогового бремени X, либо отрицательно от уровня государственных расходов на предотвращение теневой экономической деятельности Z. Переменная Y может также зависеть от обеих переменных X и Z. Получены международные данные двух перекрестных выборок по У, X и Z

(в млн долл. США): для группы из 30 индустриально развитых и для группы из 30 развивающихся стран. Исследователь оценивает регрессионные зависимости: log Y от logX и logZ; log Y только от logX; log Y только от logZ одновременно для каждой выборки, получая следующие результаты (в скобках приведены стандартные ошибки):

Переменная X положительно коррелирована с Z в обеих выборках. Требуется выбрать, какая из моделей лучше для индустриально развитых и для развивающихся стран, объяснить изменения в оценках коэффициентов и их стандартных отклонений в других моделях.

Решение. Запишем модели, оцененные по данным для индустриально развитых стран: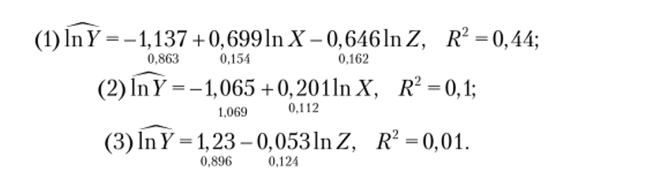

Предположим, что лучшей является модель (1), — тогда в модели (2) коэффициент при переменной пХ является смещенным. Знак смещения совпадает со знаком произведения коэффициента при невключенном факторе и ковариации включенного и невключенного факторов. P|_nZ 0, следовательно, смещение отрицательно, что мы и наблюдаем в модели (3): 0,201 < 0,699. Обсуждать модель (3) особого смысла не имеет, для нее R² = 0,01 очень мал.

Таким образом, для индустриально развитых стран уровень активности в теневой экономике зависит как от налогового бремени, так и от государственных расходов на предотвращение теневой экономической деятельности.

Аналогично запишем модели, оцененные по данным для развивающихся стран:

Проанализировав коэффициенты и их стандартные ошибки в модели (4), мы можем заметить, что коэффициент при переменной InZ незначим (при любом разумном уровне значимости), т. е. этот фактор является в модели лишним. В этом случае оценки коэффициентов при переменной пХ в моделях (4) и (5) должны быть близки (обе оценки являются несмещенными), что мы и наблюдаем. В модели (6) знак оценки коэффициента при переменной InZ коитринтуитивен (он является положительным, что означает положительную зависимость уровня активное ти в теневой экономике от уровня государственных расходов на предотвращение теневой экономической деятельности).

Таким образом, для развивающихся стран лучшей является модель (5), уровень активности в теневой экономике в этих странах зависит только от налогового бремени.

Задача 9.2. По 150 наблюдениям оценили зависимость почасовой заработной платы от пола (переменная MALE равна 1 для мужчин и 0 для женщин), длительности обучения S и возраста AGE (иод оценками коэффициентов указаны стандартные ошибки):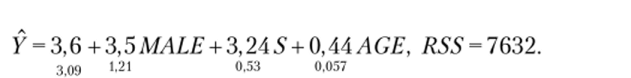

Используя результаты двух вспомогательных регрессий, приведенных ниже, проведем RESET-тест и ответим, правильная ли спецификация модели выбрана.

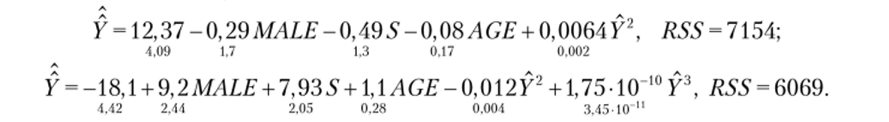
Решение. Для первой вспомогательной модели проведение теста Рамсея равносильно проверке значимости коэффициента при У². Поскольку соответствующая t- статистика равна 3,2, что меньше критического значения при уровне значимости 5%, то гипотеза Я₍₎ о правильной спецификации модели отвергается.

Для второй вспомогательной регрессии проведение теста Рамсея совпадает с проверкой гипотезы об одновременном равенстве нулю коэффициентов при У² и У³ с помощью F-статистики:

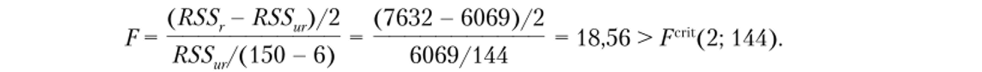
Таким образом, и в этом случае гипотеза о правильной спецификации модели отвергается.

Задача 9.3. При применении к модели, результаты оценки которой приведены ниже, метода последовательного исключения, какая переменная будет удалена из уравнения регрессии на ближайшем шаге?

. vif.

Решение. При выборе переменных метолом последовательного исключения требуется ориентироваться исключительно на p-value коэффициентов. Поскольку наибольшее р-valueу равное 0,635, у коэффициента ETHHISP, то на ближайшем шаге из уравнения регрессии будет удалена именно эта переменная.

Задача 9.4. Оценено уравнение регрессии (под оценками коэффициентов указаны значения t-статистик):

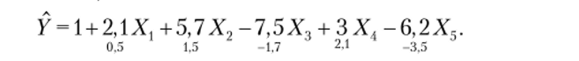
При удалении каких переменных качество подгонки регрессии может увеличиться?

Решение. Воспользуемся утверждениями 9.2, 9.3.

Поскольку t-статистика при факторе Х_х меньше 1, то в силу утверждения 9.3 качество подгонки регрессии увеличится при удалении этого фактора.

Так как V2- 1,41, а двух факторов с t-статистиками, по модулю меньшими 1,41, нет, то при удалении любых двух факторов качество подгонки регрессии не увеличится.

Так как V3 ~ 1,71, то в силу утверждения 9.2 при удаления факторов X_v X_v Х₃ (t-статистика при каждом из которых меньше 1,71) качество подгонки регрессии может увеличиться.

Четырех факторов с t-статистиками, по модулю меньшими, чем V4 = 2, нет. Точно так же нет и пяти факторов с t-статистиками, по модулю меньшими, чем V5 «2,24. Поэтому больше нет никаких вариантов.

Задача 9.5. Докажем, что оценка инструментальных переменных (9.1) является состоятельной.

Решение. Преобразуем формулу для оценки инструментальных переменных:

1 _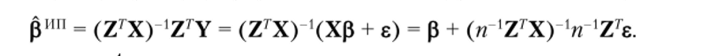

Поскольку plimZ⁷e = 0, то plim р^ип = р.

/1 — 00 п о Задача 9.6. Покажем, что если число инструментов Z_v …, Z_m превышает число объясняющих переменных X_v …, Х_к в модели Y = р_о + р, Х, + … + р_АХ* + е, то оценка инструментальных переменных, полученная с помощью двухшагового МНК, определяется формулой (9.2).

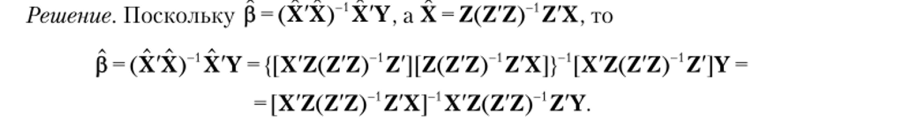
Задача 9.7. Докажем, что для модели Y = Хр + е ошибки измерения зависимой переменной Y не приводят к смещению в оценках коэффициентов р, а ошибки в измерении независимых переменных, входящих в матрицу X, приводят к смещению.

Решение. Предположим, что зависимая переменная измерена с ошибками, т. е. вместо Y у нас имеются наблюдения Y* = Y + и, где ошибки и не зависят от X и е и имеют нулевое математическое ожидание. Тогда оценивается модель Y* = Хр + е + и. Оценка коэффициентов р, рассчитываемая, но формуле р = (Х^ГХ) 'X' Y, будет несмещенной, поскольку Е ( р) = J?[(X^rX)" ¹X^r(X|р + е + и)] = р.

Если же с ошибкой измерены независимые переменные, т. е. вместо X используется матрица X* = X + V, то оценивается модель Y = Х*р + (е — VP). В этой модели регрессоры и ошибки уже коррелированы, поскольку cov (X е — VP) = cov (X + V, s — VP) т⁶ 0, т. е. имеет место проблема эндогенности, следовательно, оценки коэффициентов будут смещенными.

• [1] Задача взята из работы [10, с. 216].