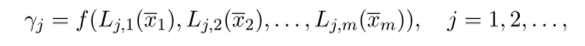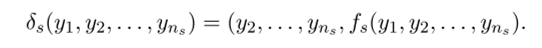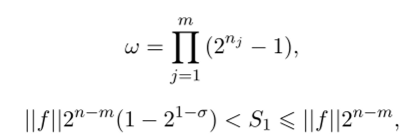Комбинирующие генераторы. 
Криптографические методы защиты информации

Комбинирующий генератор строится на основе т > 1 линейных регистров сдвига над полем ?_(/ (будем обозначать их ЛРС-1, …, ЛРС-т) и выходной функции f (xi, X2,? ??, х_т). На вход функции / подаются знаки, вырабатываемые линейными регистрами. При этом значениями переменной Xj являются знаки, вырабатываемые ЛРС-ф j = 1,…, т.

Уравнения гаммообразования для комбинирующего генератора имеют вид:

где.

• • x_s = x_St2,? ? •, x_s,_nJ — начальное состояние ЛРС-s,
• • Lj,_s(x_s) = ?i, e (<$^-1(x_s)), L_hs(yi, y₂,…, y_ns) = Уъ
• • 5_S — преобразование векторов пространства F"^s, осуществляемое ЛРС-.s:

Под начальным состоянием комбинирующего генератора понимается совокупность ненулевых начальных состояний всех входящих в него ЛРС. Известны условия, см. [5], при которых комбинирующий генератор обладает гарантированными периодом и статистическими свойствами.

Утверждение 6.13. Пусть комбинирующий генератор построен на основе т двоичных линейных регистров сдвига, имеющих максимальный период и попарно взаимно простые длины п₃, j = 1 а

также фильтрующей функции f (x,…, х_т), которая существенно зависит от каждой переменной. Пусть ш — выходной период генератора, S — число единиц на периоде. Тогда

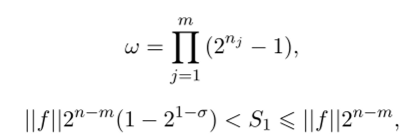
где п — Ylp=i ⁿj> ^G — ^min{nj|ji = 1,…, m}.

Для оценки линейной сложности выходной гаммы поставим в соответствие каноническому многочлену функции /(х,…, х_т) над полем F₄ многочлен fz{x,…, х_т) над кольцом целых чисел Z, полученный заменой всех ненулевых коэффициентов многочлена /(жi,…, x_m) на 1 и заменой операций в поле F₉ операциями в кольце Z.

Утверждение 6.14. Пусть L — линейная сложность гаммы комбинирующего генератора. Тогда L ^ fz (ⁿh…, п_т).

Доказательство. В соответствии с уравнениями гаммообразовапия для получения выходной функции на j-ю координату функции /(ж 1,…, х_т) поступают линейные комбинации от rij независимых переменных, j — 1,2,…, т. Поэтому после приведения подобных членов полином любой функции на выходе комбинирующего генератора будет содержать не более fz{n,…, п_т) конъюнкций. Следовательно, и ранг множества функций на выходе, совпадающий с линейной сложностью, не превышает fz (ni,…, п_т). ?

При некоторых дополнительных условиях линейная сложность гаммы комбинирующего генератора совпадает с верхней оценкой Теорема 6.7 (см. [1]). Пусть все JIPC-j, j = 1,2обладают примитивными характеристическими многочленами над полем F,_; и попарно взаимно простыми длинами, то есть НОД (щ, rij) = 1 при г Ф j. Пусть также в каноническом многочлене функции f (x,…, х_т) над полем ?_ч переменные х,…, х_т входят в степени, не превосходящей единицу, и deg / = т. Тогда линейная сложность гаммы комбинирующего генератора равна., п_т).

Кроме того, равенство L = /г{щ,… п_т) имеет место, если F₉ = F_p — простое поле и линейные регистры сдвига комбинирующего генератора имеют примитивные характеристические многочлены попарно взаимно простых степеней.