Стандарт ECDSA. 
Криптографические методы защиты информации

Американский стандарт на электронную подпись FIPS 186 вначале стандартизировал схему электронной подписи Эль-Гамаля, реализуемую в мультипликативной группе конечного простого поля и получившую название DSA (digital signature algorithm). Начиная со второй редакции данного стандарта допускается возможность реализации схемы DSA в группе точек эллиптической кривой, определенной либо над конечным простым полем F_p, либо над конечным простым полем F? характеристики 2. Такую схему принято называть ECDSA (elliptic cwve digital signature algorithm).

Далее мы дадим описание схемы ECDSA применительно к группе точек эллиптической кривой, определенной над конечным простым полем F_p. Открытые параметры такой схемы аналогичны параметрам ГОСТ Р 34.10−2012, см. раздел 11.2.1.1, за исключением используемой функции хеширования.

До последнего времени стандарт FIPS 186 предписывал использовать семейство функций SHA, вырабатывающих коды целостности длины I = 160, 256, 384 и 512 бит. Соответственно, изменение длины кода целостности приводит к изменению величины q, определяющей порядок подгруппы, которую порождает точка Р. Мы будем считать, что для q выполнено неравенство 2^[1][2] > q.

Ключевая система схемы ECDSA совпадает с ключевой системой схемы ГОСТ Р 34.10−2012, описанной в разделе 11.2.1.2.

Для выработки и проверки электронной подписи необходимо выполнить следующие действия.

Алгоритм 11.4 (Алгоритм выработки подписи ECDSA).

Вход: Параметры алгоритма a, b, p, q, P, отображение Я, сообщение s. Выход: Цифровая подпись с под сообщением s.

• 1. Вычислить значение хэш-функции от сообщения s: h = H (s), где h ? F,. Если выполнено равенство h = 0, то положить h равным 1.
• 2. Вычислить случайное число к ? {1… с/ — 1} и определить точку С=[к}Р.
• 3. Определить г = хс (mod q), где хс — х-координата точки С.
• 4. Вычислить s = k~^[2](h+dr) (mod q) и определить цифровую подпись

с равенством с = (r||s). ?

Алгоритм 11.5 (Алгоритм проверки подписи ECDSA).

Так же как и для схемы ГОСТ Р 34.10−2012, для схемы ECDSA легко проверить, что алгоритм проверки даст истинное суждение, если исходное сообщение нс изменено. Действительно, равенство точек эллиптической кривой.

дает нам равенство их ж-координаг.

Основное отличие стандарта FIPS 186 от остальных международных стандартов, регламентирующих применение электронной подписи, заключается в том, что FIPS 186 жестко определяет параметры эллиптических кривых, используемых в государственных структурах США. Каждая эллиптическая кривая, рекомендованная к использованию, определяется сравнением.

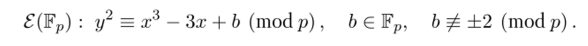
Кроме этого, стандарт в явном виде определяет г/ — порядок циклической подгруппы, в которой реализуется схема электронной подписи, а также простое число р. Ниже мы приводим список кривых, порядок группы точек которых превышает 160 бит.

• [1] Вход: Параметры схемы a, b, p, q, P, отображение Я, сообщение s и электронная подпись с. Выход: Заключение о том, верна подпись или нет.
• [2] По полученной подписи с вычислить целые числа г, s. Если выполнены неравенства 0 < г, s < q, то перейти к следующему шагу. Впротивном случае подпись неверна. 2. Вычислить значение хэш-функции от сообщения s: h = H (s), гдеh? Ff/. Если выполнено равенство h = 0, то положить h равным 1. 3. Вычислить Z = hs~2 (mod q) и Z2 = rs₁ (mod q). 4. Вычислить точку С = [zi]P + [2−2]Q и вычислить г' = хс (mode/), где хс — х-координата точки С. 5. Если выполнено равенство г' = г, то подпись принимается, в противном случае подпись неверна. ?
• [3] По полученной подписи с вычислить целые числа г, s. Если выполнены неравенства 0 < г, s < q, то перейти к следующему шагу. Впротивном случае подпись неверна. 2. Вычислить значение хэш-функции от сообщения s: h = H (s), гдеh? Ff/. Если выполнено равенство h = 0, то положить h равным 1. 3. Вычислить Z = hs~2 (mod q) и Z2 = rs₁ (mod q). 4. Вычислить точку С = [zi]P + [2−2]Q и вычислить г' = хс (mode/), где хс — х-координата точки С. 5. Если выполнено равенство г' = г, то подпись принимается, в противном случае подпись неверна. ?