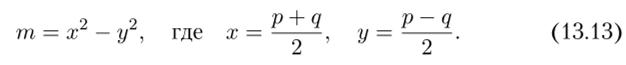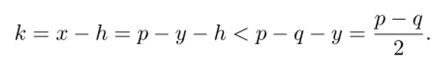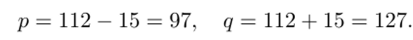Метод Ферма.
Криптографические методы защиты информации
Если величина и является полным квадратом, то закончить алгоритм, определив у = ^/v, р = х + у. Пусть гп = pq, где р, q — натуральные, не обязательно простые, делители числа т и р > q. Тогда. Алгоритм 13.5 (Алгоритм факторизации Ферма) Вход: Целое составное число т > 0. Вычислить наименьшее целое число h такое, что /г2 > у/т, то есть h = sfm. Таким образом, мы нашли х — 112 и у — 15… Читать ещё >
Метод Ферма. Криптографические методы защиты информации (реферат, курсовая, диплом, контрольная)
Авторство следующего метода приписывается известному математику Пьеру Ферма (Pierre de Fermat). Он заметил, что составное число всегда может быть представлено в виде разности двух квадратов, и предложил основанный на этом наблюдении простой способ поиска делителей.
Пусть гп = pq, где р, q — натуральные, не обязательно простые, делители числа т и р > q. Тогда.
Метод Ферма разложения на множители заключается в переборе всех возможных значений величины у и проверке является ли число т — у2 полным квадратом. Если эго условие выполнено, то делители р, q удовлетворяют равенствам р = х + у, q = х — у.
Алгоритм 13.5 (Алгоритм факторизации Ферма) Вход: Целое составное число т > 0.
Выход: 11атуральный делитель р > 1 числа га.
- 1. Вычислить наименьшее целое число h такое, что /г2 > у/т, то есть h = sfm.
- 2. Если /г2 = т, то определи ть р = h и завершить алгоритм.
- 3. Определить х = h, v = х2 — т и счетчик к = 0.
- 4. Пока к > 0 выполнять
- 4.1. Если величина и является полным квадратом, то закончить алгоритм, определив у = ^/v, р = х + у.
- 4.2. Вычислить к = к + 1, х = х + 1 и v = v + 2h + 1.? чины у = Поскольку выполнено неравенство р > h > q, мы можем оценить величину к следующим образом. Согласно шагу 4.2 приведенного алгоритма, в момент нахождения делителя выполнено равенство х = h + к, и мы получаем
Пример 13.1. Рассмотрим следующий пример и постараемся разложить на множители методом Ферма целое число т — 12 319.
Поскольку выполнены неравенства 1102 < 12 319 < 1112, мы определим h — 111 и рассмотрим последовательность чисел х = 111 + А; для чисел к = 0, 1, 2, ____Для каждого числа х определим величину х2 — т и проверим, является ли она квадратом.
к | X | X2 | x2 — rn | У |
12 321 + 2−111 + 1 = 12 544. |
Таким образом, мы нашли х — 112 и у — 15. Следовательно,.
Легко проверить, что решение найдено правильно, поскольку выполнено равенство 97 • 127 = 12 321.
Далее мы рассмотрим алгоритмы, которые позволяют эффективно раскладывать на множители числа т частного вида. В этих алгоритмах используются некоторые свойства числа т, которые существенно снижают трудоемкость разложения на множители.