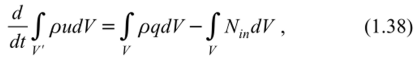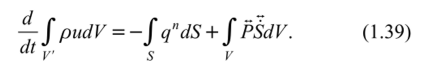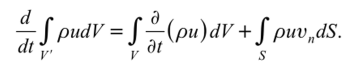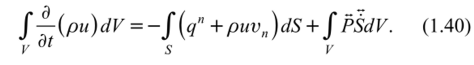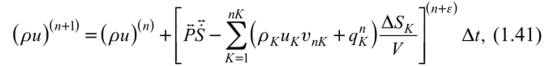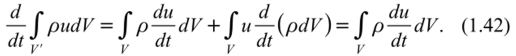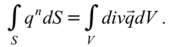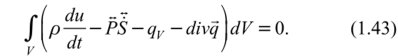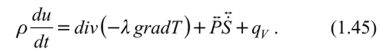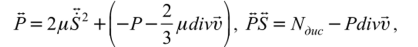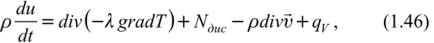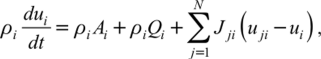Уравнение баланса внутренней энергии

Удельная внутренняя энергия и ^— определяется с.

^кг)

точностью до постоянной м₀ и часто принимается линейно зависящей от температуры Г. Для капельных жидкостей и = сТ + и₀, для калорически совершенных газов и = c_vT + и₀,

• (Дуг
• — — удельная теплоемкость жидкости,

кг-К)

I Дж

c_v — — удельная изохорная теплоемкость газа.

кгК ]

Уравнение баланса внутренней энергии в интегральной форме может быть получено вычитанием уравнения (1.23) из (1.30):

или, полагая q_v = 0, с учетом (1.31) и (1.28)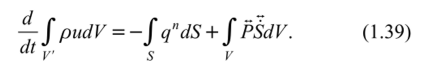

Для преобразования уравнения (1.38) в алгебраическую форму для контрольных объемов V запишем правую часть (1.39) в виде:

Тогда из (1.38) и (1.39) получим:

Область течения разбиваем на конечное число малых, но конечных контрольных объемов (КО) — V. В пределах каждого КО полагаем линейным или экспоненциальным изменение параметров по пространственным координатам и времени (§ 4). Тогда из (1.40) получим уравнение баланса внутренней энергии в алгебраической форме.

где пК — число граней контрольного объема, К — номер грани.

Для получения дифференциального уравнения баланса внутренней энергии преобразуем левую часть (1.38) с использованием закона сохранения массы.

Поверхностный интеграл в (1.40) преобразуем в объемный по формуле Остроградского-Гаусса.

Тогда из (1.37) и (1.31) получим:

Ввиду произвольности V подынтегральная функция в (1.43) равна нулю:

Используя закон Фурье q = —X gradT для теплового пото;

(Вт

ка из-за теплопроводности, где Я — — коэффициент те;

М’К)

плопроводности, получим уравнение:

Учитывая выражение для тензора напряжений для линейно вязких сред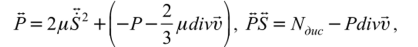

2 2.

где N_duc = 2/uS² ——/u (divv) — диссипируемая мощность, т. е. необратимая часть мощности внутренних сил с противоположным знаком, получим уравнение баланса внутренней энергии в виде:

откуда следует, что изменение внутренней энергии происходит за счет подвода тепла вследствие теплопроводности, работы сил трения при деформации жидких частиц, работы при деформации потока за счет сил давления и выделения теплоты за счет источников в потоке.

Уравнение баланса внутренней энергии /-й фазы аналогично (1.37), но включает в себя слагаемое, определяемое энергетическим взаимодействием между /'-и и г-й фазами (Вт)

Jtill — у—— I. Аналогично (1.44) выводится уравнение баланса внутренней энергии /-й фазы в дифференциальной форме.

(/ = 1,2,."У).

где Aj и Qi представляют собой работу внутренних сил и притока тепла в единицу времени, отнесенные к единице массы I-й фазы.