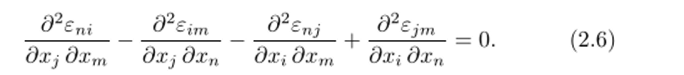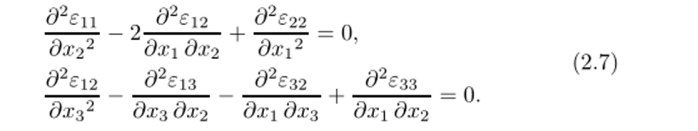Условия совместности. 
Механика сплошной среды: теория напряжений и основные модели

Компоненты тензора деформации связаны между собой соотношениями, называемыми условиями совместности деформации. При построении математических моделей механики деформируемого твердого тела можно, используя соотношения Коши для деформаций, исключить их, выразив через перемещения, и привести уравнения к вида в котором компоненты вектора перемещений будут связываться дифференциальными соотношениями. Таким образом сформулированная задача называется задачей, в перемещениях. Для такой ее постановки условия совместности не требуются, так как компоненты тензора деформаций представлены через перемещения и в явном виде не присутствуют в уравнениях. При других формулировках задачи, в которой появляются дифференциальные операторы, применяемые к компонентам тензора деформации, может возникнуть ситуация, когда построенной системе уравнений отвечает более широкий класс решений, чем это следует из физической сущности задачи. В этом случае условия совместности позволяют выделить допустимые решения, и их включение в систему уравнений необходимо.

Компоненты симметрического тензора малых деформаций Sij представляются как дифференциальные функции векторного поля перемещений eij = /2(dui/dxj—duj/dxi). В общем случае эти компоненты могут принимать произвольные значения в выбранной точке пространства, но когда мы поставим вопрос о том, как эти тензорные компоненты могут изменяться в окрестности выделенной точки, то их зависимость от компонентов исходного векторного поля щ (х 1,#2>#з) выдвинет определенные ограничения. Сущность этих ограничений состоит в том, что, дважды продифференцировав по координатам компоненты тензора деформации, мы выразим эти производные через третьи производные компонентов вектора перемещений. Требование согласованности этих дифференциальных представлений приводит к системе соотношений вида.

Из них только шесть являются независимыми и называются условиями совместности Сен-Бенина для малых деформаций. Два первых соотношения имеют вид.

Остальные четыре условия совместности получаются из этих циклической перестановкой индексов (1, 2, 3) —> (2, 3, 1) —> (3, 1, 2).

В данном случае были выписаны условия совместности для малых деформаций, однако такого же типа условиям должны удовлетворять и компоненты тензоров конечных деформаций Грина и Альманси.

Условия совместности появляются и в других задачах, где связываются дифференциальным образом параметры, которые, в свою очередь, получены из некоторого непрерывного ноля. В частности, в задаче о движении несжимаемой жидкости роль условия совместности поля скоростей точек материальной среды выполняет уравнение неразрывности divv = 0. По аналогии иногда соотношения (2.7) называют уравнениями неразрывности для деформаций.