Система параллельных сил

Силы называются параллельными, если линии их действия параллельны между собой.

Наиболее простым случаем является система из двух параллельных сил (рис. 2.12, а).

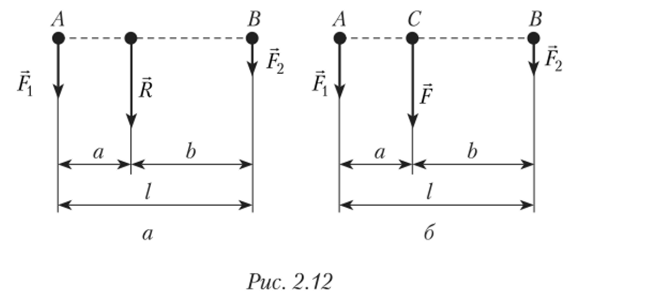
Равнодействующая двух параллельных сил равна по величине их сумме R = F_] + F₂, параллельна им, и линия ее действия делит прямую, соединяющую точки приложения сил, на части, обратно пропорциональные величине.

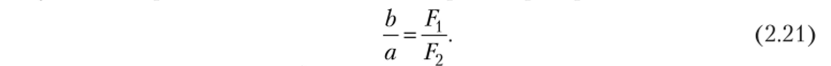
Для разложения силы F на два направления (рис. 2.12, б), т.с. получения двух сил F_{ и F₂, необходимо воспользоваться соотношениями.

Центр параллельных сил. Центром системы параллельных сил называют точку приложения их равнодействующей.

Равнодействующая системы параллельных сил равна алгебраической сумме составляющих сил и параллельна им:

Линию действия равнодействующей можно определить при последовательном сложении составляющих сил, когда на основании (2.21) можно определить положение результирующей при сложении двух сил. Данный прием достаточно прост, но очень трудоемок при большом количестве действующих сил.

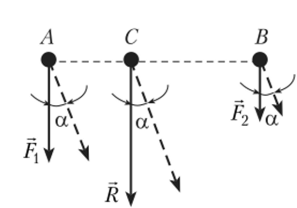
Рис. 2.13.

Рассмотрим простейший случай двух параллельных сил (рис. 2.13). К телу в точках А и В приложены две параллельные силы Р_{ и Р₂. Равнодействующая R, определенная на основании (2.21), очевидно, будет приложена в точке С, лежащей на прямой АВ. Повернем обе силы около точек их приложения на угол, а (силы после поворота показаны на рис. 2.13 пунктиром). Величина равнодействующей не изменится, она тоже повернется на угол, а и будет проходить через ту же точку С. Точка С является центром параллельных сил Р_х и Р₂. Как бы ни поворачивались точки силы Р_{ и Р₂ вокруг точек своего приложения, их равнодействующая будет проходить через этот центр.

Применяя последовательно правило сложения двух параллельных сил, можно показать, что описанное свойство справедливо для любого количества параллельных сил, и из него следует порядок определения их центра:

• — найти линию действия равнодействующей параллельных сил;
• — все силы системы повернуть на один и тот же угол;
• — для нового положения сил снова найти линию действия равнодействующей;
• — точка пересечения линий действия равнодействующих в двух положениях системы сил и определит центр этой системы.

Аналитическое определение координат центра параллельных сил покажем, рассмотрев систему сил P_v Р_2> F₃, Р_А, … (рис. 2.14), имеющую точки приложения сил с известными координатами А (х_х, у_х)_у А₂(х₂, у₂), А₃(х₃, г/₃), А_л(х_4у у_А) и т. д.

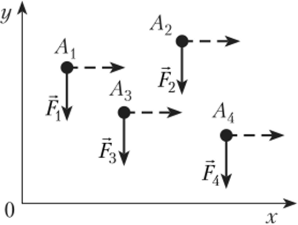
Рис. 2.14.

Найдем точку С (х_с, у_с), через которую должна пройти равнодействующая R = F + Р₂ + F₃ + F_a +… = X Fj.

j=i.

По теореме Вариньона (2.17) сумма моментов сил системы относительно начала координат равна моменту равнодействующей относительно него же:

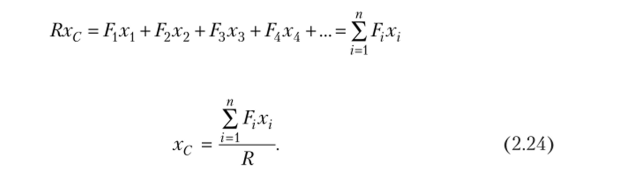
откуда Теперь повернем все силы на угол, а = 90° вокруг точек их приложения и снова применим теорему Вариньона:

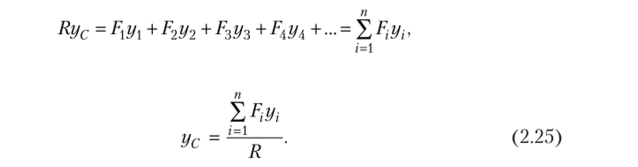
откуда Подставив в (2.24) и (2.25) выражение (2.23), получим.

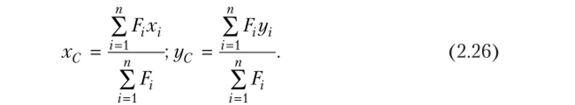
Формулы (2.26) определяют положение центра системы параллельных сил.

Если нет необходимости знать точку приложения равнодействующей параллельных сил, а необходима только линия ее действия, используется одна из формул (2.26), в зависимости от направления системы параллельных сил.

В инженерных расчетах одним из часто встречающихся видов систем параллельных сил являются распределенные нагрузки. На рис. 2.15 показаны величины равнодействующих и их положение на участке загружения для двух наиболее простых видов таких нагрузок в плоскости: равномерно распределенной (рис. 2.15, а) и треугольной распределенной (рис. 2.15, б).

Уравнения равновесия параллельных сил. В случае, когда все силы параллельны, одну из осей координат, например ось у, можно направить параллельно силам. Так как все силы имеют нулевые проекции на ось х, а на ось у проецируются без искажения, то проекция главного вектора равна алгебраической сумме сил:

Формула для определения главного момента (2.17) останется неизменной, а количество уравнений равновесия уменьшается до двух.

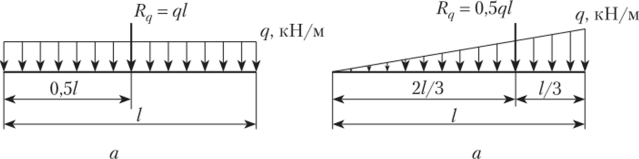
Рис. 2.15.

Первая форма уравнений равновесия примет вид

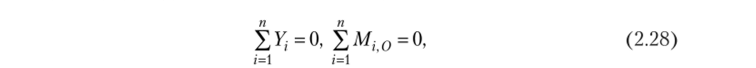
а вторая форма уравнений.