Существование древовидного оптимального ИГ для задач поиска с коротким ответом

В этом пункте мы докажем теорему о существовании древовидного оптимального графа для задач, обладающих А-свойством.

Скажем, что вершина, а графа схемно достижима из вершины 0, если из 0 в, а существует ориентированная цепь.

Пусть 0 — вершина некоторого ИГ. Обозначим через Vp множество записей, соответствующих листьям, схемно достижимым из вершины 0.

Скажем, что ИГ обладает С-свойством, если для любой вершины 0 ИГ, за исключением корня <�рр = ] Ху р-

V€V*.

Пусть I = (X, V, p) — некоторая ЗИП, где V = {yi, 2/2, —, УАг}> тогда обозначим.

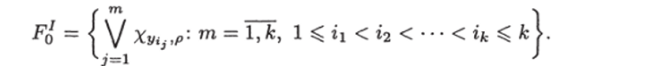
Скажем, что ИД над базовым множеством Т = (Fq, 0) обладает Djсвойством, если оно разрешает ЗИП I, обладает С-свойством и у любой вершины ИД, не являющейся полюсом, полустепень исхода больше 1.

Обозначим через V¹ множество всех ИД, обладающих Dj -свойством.

Справедлива следующая теорема [24].

Теорема 6. Пусть I = {X, V, p) — ЗИП, Т — (F, 0) — произвольное измеримое базовое множество, допустимое для I, U — произвольный ЛИГ над базовым множеством Т, разрешающий ЗИП I. Тогда,

• • если I обладает A-свойством, то существует ИД D € V¹, такое, что T (D) ^ T (U),
• • если I обладает Всвойством, то существует ИД D 6 V¹, такое, что T (D) ^ T (U).

Доказательство. Обозначим через.

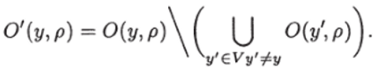
Понятно, что если / обладает В-свойством, то 0'(у, р) = 0(у, р), а если I обладает A-свойством, то Р(0'(у, р)) = Р (0(у, р)).

Обозначим через Fi следующее бесконечное множество предикатов.

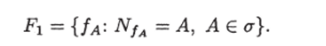
Отметим, что так как Т измеримо, то F С F. Если I обладает А-свойством, то поскольку а — алгебра, то Fq С Fi.

Скажем, что ПИГ над базовым множеством (Fi, 0) обладает Е-свойством, если он разрешает ЗИП I и для любого листа ПИГ полустепень исхода этого листа равна 0.

Покажем, что существует ОИГ Uq, обладающий Е-свойством, такой, что T (Uo) ^ T (U).

Пусть С — (аьаг)(о:2"аз) * * • («г-ь^г) — цепь в ПИГ, где — корень ПИГ. Множество ребер, исходящих из вершин а^аг,…, <*г-ь назовем следом цепи С, а множество ребер, исходящих из вершин с*2, • • •, a_r_i — усеченным следом цепи С. Соответственно число п =.

г—1.

= $ 3 'Фон будет мощностью усеченного следа цепи С.

1=2.

Пусть V = {з/i, у₂, — •, УАг}- Рассмотрим сначала запись у.

Обозначим через С_ух = {С, Сг,…, С_т} — множество цепей, ведущих из корня в листья множества Ьи (у). Пусть функции проводимости цепей С,…, С_т соответственно. Так как U разрешала т

ет /, то согласно теореме 1 V /" = Xy_t, pi или U ^f% ⁼

«=1 *=i.

Выберем в С_У1 подмножество цепей, такое, что характеристические множества их функций проводимости образуют тупиковое покрытие О^г(у, р). Без ограничения общности можно считать, что это первые s

з

цепей (s ^ т), т. е. |J Nf. D 0'{у, р), но удаление любого множества *=1.

из объединения в левой части нарушает данное соотношение.

Пусть N[ С N/_i (i = l, s), такие, что N[ П N’j = 0, если i ф j

{i, j G {M}) и (J N- = 0'{уиР).

t=l.

Понятно, что такие N[ (г = l, s) можно подобрать.

Обозначим через щ мощность усеченного следа цепи (7* (г = 1, т). Пусть с ребро ПИГ, через [с] будем обозначать его нагрузку, т. е. предикат, приписанный этому ребру.

Для каждого ребра с графа U заменим его нагрузку [с] на fN_[c]'(y_up) — ^{Так как} Л[е) G О И О'(уьр) G <7, ТО /лГ_(е)'(У1,р) <= F.

После такой операции функции фильтра листьев, не принадлежащих Lu (yi), не изменятся, а дизъюнкция функций фильтра листьев из Ьи (у) станет равной /о (у_1}р)оЦу1, р)1 ^ПР^И этом сложность графа.

s

уменьшится по крайней мерс на ' P (N/).

Пусть nj = min щ. *⁼¹

Пусть цепь Cj ведет в некоторый лист ас € Ьи{у{). Все листья из Ьц (у), отличные от ац, объявим обычными вершинами и уберем приписанную им нагрузку у. После этой операции множество Lu (y) будет состоять только из одного листа а.

Для каждого ребра с цепи Cj заменим его нагрузку [с] на [с] Vx_yi, pПосле этой операции функция фильтра листа а станет равной ip_Ql = = Xyi, p- Таким образом, полученный граф снова решает задачу I.

В результате последней операции сложность графа увеличится на n,-P (0(yi, p)).

Заметим, что.

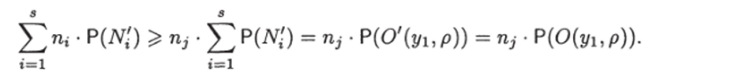
Отсюда следует, что полученный граф по сложности не больше чем T (U).

Псреобозначим цепь Cj на С[.

Проделаем выше описанную процедуру для всех остальных записей jft, i = 2, fc, и для каждой записи з/, получим цепь С,-, ведущую из корня в некоторый лист а* (причем а* будет единственным листом в Ьц (у{)) и имеющую проводимость Ху", р;

Удалим из полученного графа все ребра, не принадлежащие ни одной из цепей С{,…, С'_к. Граф U получающийся после этого удаления, будет разрешать задачу I и иметь сложность, не превышающую T (U).

Отметим, что В-сложность полученного U если I обладает В- свойством, также не увеличится. В самом деле, для любого х € € Х (у, р) выполняется T (U, x) = T (Ux)_y а для любого х G 0(у, р) справедливо T (Ux) = rij + ip_ri где гр_г — число ребер, исходящих из корня, тогда как T (U, х) ^ rij + гр_г для этих х.

Граф U' является О ИГ, так как каждой записи соответствует ровно один лист. Покажем, что в графе U¹ полустепень исхода любого листа равна 0.

Предположим, что это не так. Так как граф U' состоит только из ребер, принадлежащих цепям С (,…, С?, то, значит, некоторая цепь C’j (j? {1, А:}) проходит через некоторый лист а_ш, где т € {l, fc} итф j. Так как граф U' разрешает ЗИП /, то </?_ат = Ху_т, рСледовательно, проводимость fj цепи Cj такая, что Nf_j С 0(г/_ш, р). Но этого не может быть, так как Nf_j = 0(yj, p) и либо Р(0(yj, p) ПО (у_ш, р)) = = 0, и P (0(yj, p)) ф 0, если ЗИП I обладает Л-свойством, либо 0(yj, p) П 0(у_т«р) = 0, и 0(yj, p) Ф 0, если ЗИП I обладает В- свойством.

Таким образом, мы доказали, что U' обладает Е'-свойством и, значит, его можно взять в качестве искомого графа Uq.

Теперь в графе Uo изменим нагрузку всех ребер следующим образом. Пусть с произвольное ребро графа, такое, что оно принадлежит цепям С[_г,…, C'_irn, тогда в качестве нагрузки этого ребра возьмем.

m.

V Xy_t р G Fq. В частности нагрузка ребра, ведущего в некоторый j=1.

лист а*, будет равна у

Поскольку эта замена не меняет проводимости ни одной из цепей …,С'_к} то функционирование графа не меняется.

Граф, полученный после осуществления такой замены нагрузки для всех ребер, обозначим через U. T (U) ^ T (Uо), так как в графе Uo для каждого ребра, принадлежащего С[ (г € {l, fc}), конъюнкция его нагрузки и функции Xy_itp равна Ху*, р;

ОИГ Ui является графом над Fq, T (U) ^ T (U), U обладает F-свойством, причем в каждый лист графа U ведет единственное ребро, и еще, если 0 вершина графа Uu отличная от корня, через Л.

которую проходят некоторые цепи С[_х,…, С[_а, то <�рр = V Xy_ij, р •.

Причем так как через эту вершину /3 не проходит других цепей, ведущих в листья, то V# = {у*,.•, у"Л> откуда следует, что ОИГ U обладает С-свойством.

Предположим, что в U есть вершины с полустепенью захода более 1. Пусть этих вершин т штук.

Рассмотрим произвольную вершину 0 с полустепенью захода, превышающей 1.

Пусть через нее проходит s цепей CJ ,…, С[_а. Согласно замечанию Л.

VP = V Xyi., p•.

j=l.

Отметим, что ребра, входящие в вершину 0 не принадлежат никаким другим цепям, кроме цепей С[ ,…, С[₉.

Обозначим через С" , и С" ' части цепи С. (j 6 {1,5} соответственно от корня до вершины 0 и от вершины 0 до листа, а через п. — мощность усеченного следа цепи С". Обозначим через Gp подграф Л.

графа Ui, состоящий из цепей С" _х,…, С", а через Op = (J 0'(у{., р).

i=1.

Для каждого ребра с подграфа Gp заменим его нагрузку [с] на In_[c)o₀— Н^е трудно заметить, что после этой операции проводимости цепей С'_т, таких, что тп ? {1, не изменится, более того нагрузка ребер из этих цепей, как и прежде, будет принадлежать Fq. При этом л.

сложность графа уменьшится по крайней мере на • Р (0'(у,_я/э)).

*=1.

Пусть п, = min п .

Для каждого ребра с цепи С" _{ (j = 1,5) заменим его нагруз;

ку [с] на [с] V V Хуг₄, р• Эта замена увеличит сложность графа на.

j=1.

ⁿt, ‘ P (0(y*,->P))i ^н0 поскольку это меньше чем J2 ⁿ_j *.

i=i.

то полученный граф по сложности не превышает T (U).

Объявим цепью С[. цепь, составленную из C" _t и С" ' (j = 1, s). Нетрудно заметить, что проводимость новообъявленных цепей С- попрежнему равна Xyi_j, р •.

Теперь удалим все ребра, не принадлежащие ни одной из цепей С'.

(j = 1,к). В частности мы удалим все ребра, входящие в вершину /3, кроме ребра, принадлежащего С", в силу сделанного выше замечания о ребрах, входящих в 0.

Полученный таким образом граф обозначим (/2- Мы получили, что T (U2) ^ T (U), U2 разрешает задачу /, и число вершин с полустепенью захода более 1 в U2 по крайней мере на 1 меньше чем в U, поскольку теперь в вершину (3 ведет единственное ребро, а новых вершин с полустепенью захода более 1 образоваться не могло.

Нетрудно заметить, что T (U2) ^ T ([/i). В самом деле, для любого х е X Ор имеем T (U2, x) = T (U, x), а для любого j Е {1,5} и для любого х € 0(ух₅, р) получаем T (U2, x) = T (U, x) — п. + n'_it ^ ^T (U_ux).

Применяя вышеописанную процедуру к графу (/2, мы получим граф U3 с еще меньшим числом вершин с полустепенью захода более 1.

Применив данную процедуру нужное количество раз, мы получим некий граф U_r (г ^ га + 1), в котором полустепень захода любой вершины равна 1.

Поскольку плюс к этому полустепень исхода любого листа U_r равна 0, то U_r является информационным деревом. По построению для любой некорневой вершины графа U_r выполняется условие ipp = = V Ху, р- Предположим, что в U_r есть неполюсная вершина /?, полуy€Vfe.

степень исхода которой равна 1. Тогда нагрузка ребер, входящего в /3 и исходящего из /3, одинакова. Следовательно, ребро, исходящее из /3, можно удалить без ущерба для функционирования и сложности. Эту операцию повторим для каждой неполюсной вершины, полустепень исхода которой равна 1. После этого U_r будет ИД, обладающим Dj- свойством. Поскольку T (U_r) ^ T{U) и T (U_r) ^ Т (77) по построению, то U_r можно взять в качестве искомого дерева D.

Тем самым теорема доказана.

Следствие 1. Если ЗИП I обладает А-свойством (обладает Вi-свойством), Т = (F, 0) — измеримое базовое множество, допустимое для I, такое, что F₀⁷ С F, то существует оптимальный (В-оптимальный) ЛИГ U для ЗИП I, принадлежащий классу V¹.

Доказательство. Так как Fg С F, то V¹ С U (I, F), т. е. оптимальные ИГ, если они существуют, надо искать согласно теореме б в классе.

V¹. Чтобы показать существование оптимального ИГ, достаточно заметить, что V¹ — конечное множество. В самом деле, ИГ из D¹ — это деревья с к концевыми вершинами (здесь к — количество записей в библиотеке задачи /), нагрузка ребер которых берется из конечного множества F₀^;, значит, V¹ — конечное множество.

Тем самым следствие доказано.