Информационно-графовая модель данных

Понятие информационного графа (ИГ)

Управляющая система, функционирующая в среде, — это центральное понятие кибернетики.

Управляющие системы можно разбить на два класса: те, которые действуют без памяти (рефлекторно), и те, которые имеют память. Второй класс неизмеримо богаче, чем первый, и изучается в первую очередь. Примеры управляющих систем без памяти: вирусы, микробы, разменные аппараты. Высшие животные, человек, адаптивные системы в технике, компьютеры — управляющие системы с памятью. Естественно возникает вопрос оптимальной организации памяти в таких системах, которую можно отождествить с содержательным пониманием баз данных.

База данных (БД) — формализованное представление информации, удобное для хранения и поиска данных в нем. Понятие БД возникло в 60-е годы XX века и связано с развитием вычислительной техники и информатики. Тематика теории БД связана с поиском удобного представления, компактного хранения, быстрого поиска, защищенности и других свойств данных. Развитию этого направления способствовали как производственные и творческие коллективы: IBM (иерархическая модель данных), Рабочая группа по БД Ассоциации по языкам систем обработки данных — CODASYL (сетевая модель данных), исследовательская группа по системам управления БД Американского национального института стандартов — ANSI/SPARC Study Group on DataBase Management Systems (принципы проектирования БД), так и отдельные исследователи: Кодд (Е. F. Codd) (реляционная модель данных), Галлейр (Н. Gallaire), Минкер (J. Minker) (дедуктивные БД), Тальхайм (В. Thalheim) (моделирование семантики в БД, теория ограничений целостности), Аткинсон (М. Atkinson), Бири (С. Beeri) и др. (объектно-ориентированные БД), В. Н. Решетников (алгебраическая модель информационного поиска), Думи (A. Dumey), А. П. Ершов (методы хеширования), Бентли (J. L. Bentley), Кнут (D. Е. Knuth), Ли (D. Т. Lee), Маурер (W. D. Maurer), Ульман (J. D. Ullman), Шеймос (М. I. Shamos) и др. (сложность алгоритмов обработки данных), Э. Э. Гасанов (информационно-графовая модель данных, сложность алгоритмов поиска) и многие другие.

Основные виды представления (модели) данных сформировались под влиянием практики с использованием средств математики.

В основу реляционной модели данных [130−136, 138, 69] положено понятие отношения. Подмножество R С D х D₂ х • • • х D_n есть отношение арности п с доменами Di, D2,…, D_n. Рассматриваемые отношения, как правило, конечные, поэтому удобно представлять их в виде плоских таблиц. Строки таблицы называются кортежами, а столбцы — атрибутами. Подмножество атрибутов отношения называется ключом, если проекция таблицы на это множество состоит из разных строк, но удаление любого атрибута из ключа нарушает это свойство. Понятие ключа соответствует тупиковому тесту, поэтому результаты, полученные в теории тестов (А. Е. Андреев [6−8], А. Д. Коршунов [58], В. Н. Носков [79−82] Г. Р. Погосян [84] и др.) могут быть использованы для оценки мощности ключа и минимального числа атрибутов в ключе. Оценивались мощности ключей в случайных БД (таблицах) (О. Б. Селезнев, Б. Тальхайм [92, 201, 202] и др.). Реляционная БД —- это множество таблиц, обогащенное операциями объединения, пересечения, разности, декартова произведения, проекции, соединения, селекции, частного и др. Изучение этих алгебр отношений составляет содержание теории реляционных БД. Ассоциируемый с табличным представлением способ хранения данных не компактен, а способ поиска — полный перебор. В связи с этим в современных реляционных БД реляционная модель используется только как внешнее представление, т. е. представление пользователя, тогда как внутреннее представление данных, т. е. представление на машинных носителях, — принципиально другое. Простота представления при сохранении всех функциональных возможностей БД делают реляционную модель удобной для изучения качественных свойств и характеристик БД. Наглядность и простота понимания — причина популярности этой модели среди большинства пользователей.

Если в табличном представлении произвести лексикографическое упорядочение и сделать склейку по совпадающим префиксам, то получается древовидное представление данных, в основе которого лежит понятие дерева. Такое представление ведет к большей компактности данных и к ускорению поиска нужных данных. Такие древовидные структуры, как бинарные деревья, 2−3-деревья, В-деревья, сортирующие деревья [10] используются для внутреннего представления данных. Древовидное представление удобно использовать в лингвистических и подобных им БД, например, когда надо найти то или иное слово. В случае поиска множества однокоренных слов, т. е. слов с заданной средней частью, древовидное представление не очень удобно. Древовидное представление все еще достаточно просто для понимания, хотя и не так наглядно как табличное. При использовании древовидной (или иерархической) модели данных как внешнего представления данных предполагаются иерархические отношения между данными, т. е. отношения типа родитель-потомки, когда у каждого объекта только один родитель, но может быть несколько потомков. Такие отношения принято изображать в виде дерева, где ребро между объектами отображает наличие некоторого отношения, причем название отношения пишется на ребре. Например, между объектами «клиент» и «заказ» может быть отношение, которое называется «делает», а между «заказ» и «товары» — отношение «состоит из» Одной из систем, использующих иерархическую модель данных, является система IMS фирмы IBM [137, 169−171].

Обобщение понятия дерева до графа аналогично переходу от древовидного к сетевому представлению данных. При векторном виде данных в древовидном представлении склейка данных может быть сделана только по начальному отрезку; в сетевом представлении она допустима по любым отрезкам. В сетевой модели данных доступ к данным может быть осуществлен по многим путям. Она позволяет реализовать более широкий класс отношений между объектами, чем древовидная. Эта модель данных развивается ассоциацией CODASYL [53, 127−129]. Поскольку сетевая модель является обобщением древовидной, то она предоставляет больше возможностей как для описания предметной области, представляемой БД, так и для нахождения оптимальных решений хранения и поиска данных. Но использование сетевой модели требует высокой квалификации от разработчика и поэтому она не была воспринята массовым пользователем.

В объектно-ориентированной модели данных [ПО], опирающейся на принципы объектно-ориентированного программирования, каждый объект представляется как черный ящик, доступ к данным которого осуществляется только через специальные функции, прилагаемые к нему. Из таких ящиков строятся более сложные объекты, которые в свою очередь могут служить новыми ящиками для построения объектов следующего уровня сложности и т. д. Главное преимущество объектно-ориентированной модели — ее технологичность, в связи с чем это одна из наиболее развивающихся моделей сегодня.

Под влиянием математической логики строится дедуктивная модель данных [187]. Данные в дедуктивных базах данных рассматриваются как аксиомы, а новые данные получаются из аксиом путем логического вывода. Преимущество этой модели — компактность начального множества данных (все зашито в аксиомы и правила вывода) и потенциальная бесконечность множества выводимых фактов. Недостаток — большие ресурсы по времени и памяти, необходимые для процесса вывода. Дедуктивные базы данных удобно использовать в системах принятия решений, когда заранее не очерчена область возможных ситуаций.

Работа с БД предполагает создание удобных языков — языков манипулирования данными, примеры которых доставляют формальные языки логики и алгебры. В алгебраических языках манипулирования данными запрос к БД определяет последовательность операций, которые приведут к ответу. Такими языками являются ISDL и АСТРИД [69, 99]. В языках манипулирования данными, основанных на исчислении предикатов, запрос к БД соответствует формуле некоторой формально-логической теории, а ответом является множество объектов из области интерпретации, на котором истинна формула, соответствующая запросу. Такими языками являются QUEL, SQL, QBE [69, 99).

Тематика теории БД связана со следующими основными направлениями.

Первое в основном опирается на аппарат формально-логических теорий и связано с изучением качественных свойств моделей данных и их семантическим обоснованием. К этому же направлению относятся вопросы выразительности и сложности языков запросов, соответствующих моделям данных, изучение БД как теорий (например, в интуиционистской логике высшего порядка), а также теория ограничений целостности [208]. В ней изучаются ограничения, накладываемые предметной областью, определяющие связи между компонентами БД и описывающие поведение БД во времени. Ограничения целостности могут быть использованы в качестве языка описания семантики БД. Изучаются особого вида ограничения целостности, называемые зависимостями. Они делятся на статические (отражающие семантику всех возможных состояний БД) и динамические (описывающие поведение БД во времени, т. е. корректность последовательностей ее состояний). Изучается проблема выводимости некоторой данной зависимости из заданного списка зависимостей. Выделены классы зависимостей, в которых эта проблема неразрешима и Рили NPразрешима. При разрешимости проблемы выводимости актуальной становится задача об аксиоматизации соответствующего класса зависимостей. Известны случаи аксиоматизируемых и неаксиоматизируемых классов.

Специальное направление в теории БД составляет защищенность данных от случайного или преднамеренного доступа к ним несанкционированных пользователей [12]. Интенсивное развитие всемирной компьютерной сети Internet делает это направление особенно актуальным.

Третье основное направление тематики теории БД связано с вопросами сложности алгоритмов обработки данных. И именно к этому направлению относится данная монография.

Это направление связано с проблематикой физической организации баз данных. При физической организации баз данных мы имеем дело не с представлением данных в прикладных программах, а с их размещением на запоминающих устройствах.

Критерии, определяющие выбор физической организации, отличаются от тех, которые определяют выбор логической организации данных. При выборе физической организации решающим фактором является эффективность, причем согласно Дж. Мартину [68] на первом месте стоит обеспечение эффективности поиска, далее идут эффективность операций занесения и удаления и затем обеспечение компактности данных.

Методы физической организации данных хорошо изложены в классических книгах Д. Кнута [56], Дж. Мартина [68], А. Ахо, Дж. Хопкрофта, Дж. Ульмана [10].

Уже на самых ранних ступенях развития математики в ней стали возникать различные вычислительные процессы чисто механического характера; с их помощью искомые величины ряда задач вычислялись последовательно из данных исходных величин по определенным правилам и инструкциям. Со временем все такие процессы в математике получили название алгоритмов. Интуитивное понятие алгоритма, состоящее с перечислении черт, характерных для понятия алгоритма, можно найти в [57, 67]. До тех пор пока перед математиками стояла проблема доказательства существования того или иного алгоритма, а это можно сделать путем фактического описания процесса, решающего задачу, то интуитивного понятия алгоритма было достаточно, чтобы удостовериться, что описанный процесс есть алгоритм. Но когда в XX веке возникли алгоритмические проблемы, существование положительного решения которых было сомнительным, появилась потребность в точном определении понятия алгоритма, чтобы доказывать несуществование алгоритма. Точное понятие алгоритма было определено в трудах Поста [192] и Тьюринга [209] введением машин Тьюринга, на которых оказалось возможным осуществить или имитировать все алгоритмические процессы, которые фактически когдалибо описывались математиками.

Введение

такого объединяющего понятия как машина Тьюринга дало сильнейший толчок к развитию теории алгоритмов.

Вообще в математике типична ситуация, когда введение некоторого объединяющего понятия, которое раскрывает существенные черты, некоторых классов объектов и процессов и позволяет объединить их в едином подходе, дает ощутимый толчок в развитии новой области.

Другим примером объединяющего понятия является свойство деком позируемости функции [9], с помощью которого удалось накрыть понятия сложности функции в таких разных управляющих системах, как схемы из функциональных элементов, контактные схемы, вентильные схемы, формулы, и добиться существенного прорыва в теории сложности функций.

В данной работе также хотелось бы разработать такую модель, которая бы выявила особенности алгоритмов решения задач поиска, позволила исследовать их сложностные характеристики и объединила все наиболее известные классы задач поиска.

В понятие задачи поиска исследователи вкладывают по крайней мере 3 различных смысла.

Специалисты в теории исследования операций понимают задачи поиска как задачи управления сближением одной системы (поисковой) с другой (искомым объектом) по неполной априорной информации. Понимается, что цель поиска — это обнаружение искомого объекта, определяемое как выполнение определенных терминальных условий. Интенсивно проблемой поиска подвижных объектов начали заниматься в период Второй мировой войны. Интерес к этой проблеме в тот период был вызван необходимостью разработки тактики борьбы против подводных лодок. Среди работ, посвященных этой тематике, можно выделить, например, работы В. А. Абчука, В. Г. Суздаля [1],.

О. Хеллмана [102] и Д. П. Кима [55].

Другое понимание задач поиска можно найти в книге Р. Альсведе, И. Вегенера «Задачи поиска» [5]. Приведем поясняющий пример из этой книги.

Во время Второй мировой войны все призываемые в армию США подвергались проверке на реакцию Вассермана. При этом проверялось, есть ли в крови обследуемого определенные антитела, имеющиеся только у больных. Во время этого массового обследования было замечено, что разумнее анализировать пробу крови целой группы людей. Если такая объединенная проба крови не содержит антител, то, значит, ни один из обследуемых не болен. В противном случае среди них есть хотя бы один больной. Хороший алгоритм поиска для этой задачи — это тот, который для типичной выборки людей позволяет «наискорейшим образом» выявлять множество всех больных.

Другой пример мы находим в статье Д. Ли, Ф. Препараты «Вычислительная геометрия» [64]. Дано множество горизонтальных и вертикальных отрезков. Надо найти все точки пересечения отрезков.

Эти два примера объединяет то, что в обоих случаях поиск производится однократно. Это порождает свои особенности таких задач поиска. Как правило, данные в этих задачах не имеют сложной организации. Фиксация множества, в котором производится поиск, однозначно определяет множество найденных объектов. «Хорошесть» алгоритма поиска определяется при варьировании множества, в котором производится поиск.

В третьем понимании задачи поиска предполагается многократное обращение к одним и тем же данным, но возможно каждый раз с разными требованиями к искомым объектам, т. е. с разными запросами на поиск. Такие задачи поиска обычно возникают в системах, использующих базы данных. Многократное использование порождает особую проблему — проблему специальной организации данных, направленной на последующее ускорение поиска. Процесс такой специальной организации данных, проводимый до того, как осуществляется поиск, называется предобработкой и часто может занимать очень большое время, которое затем окупается сторицей в результате многократности поиска. Простейшим примером предобработки является сортировка. Построение «хорошего» алгоритма поиска в этом случае сводится к нахождению хороших структур данных, т. е. к осуществлению такой хорошей предобработки данных, которая обеспечила бы хорошую скорость поиска. «Хорошесть» алгоритма поиска в этом случае определяется варьированием запроса на поиск, например, как среднее время поиска на запросе. Такую же классификацию задач поиска на однократные и многократные можно найти также в [86, 193].

В зависимости от того, является ли база данных фиксированной или изменяется на протяжении времени работы с ней, мы имеем два типа организации баз данных: статическую и динамическую соответственно.

Задачи поиска, возникающие в статических базах данных и предполагающие многократное обращение к одним и тем же данным, и являются объектом исследования в данной работе.

Приведем примеры таких задач поиска.

Простейшим и самым распространенным примером задачи поиска, встречающейся в любой базе данных, является задача поиска по ключу. Суть ее состоит в том, что любой объект в базе данных имеет свой уникальный ключ. Это может быть порядковый номер, уникальное имя, или уникальное значение некоторого поля, например, номер паспорта. Задача состоит в том, чтобы по заданному в запросе ключу найти в базе данных объект с этим ключом (если такой объект в базе имеется). Более формально эту задачу можно поставить следующим образом. Имеется некоторое конечное множество ключей. Имеется некоторое более широкое множество запросов. Требуется, но произвольному запросу из множества запросов найти в множестве ключей ключ идентичный (равный) ключу-запросу. В такой постановке эта задача называется задачей поиска идентичных объектов.

Другой пример взят из систем машинной графики, обработки изображений и систем автоматизированного проектирования [64, 83, 101, 177, 189]. Дано конечное множество точек из отрезка [0,1] вещественной прямой. Множество запросов есть множество всех отрезков, содержащихся в [0,1]. Надо для произвольного запроса [u, v] из множества запросов перечислить все точки из нашего множества точек, которые попадают в отрезок [гл, v], Эта задача носит название одномерной задачи интервального поиска.

Если мы хотим всерьез изучать сложность алгоритмов поиска, то без введения математической модели объекта изучения нам не обойтись.

Поэтому начнем с формализации понятия задачи информационного поиска (ЗИП). В работах [10, 64, 87, 93, 117, 197] вводились различные формализации ЗИП. Так, в [117, 197] вводилась формализация наиболее близкая к той, которую мы будем использовать в данной работе. Формализация ЗИП в [117, 197] вводилась следующим образом: вопрос к базе данных представляет некоторый запрос, имеющий тип Т1, сама база данных состоит из элементов типа Т2, а ответ на вопрос — значение типа ТЗ, например, ТЗ может иметь логический тип, если предполагается, что ответ на запрос должен быть «да» или «нет», ТЗ может совпадать с Т2, если ответом на запрос является элемент базы данных, и, наконец, ТЗ может быть множеством элементов типа Т2, если в ответ на запрос надо перечислять некоторые элементы из базы данных. Вопрос Q рассматривается как отображение из Т1 и множества подмножеств Т2 в ТЗ, т. е. Q: Т1 х 2^ —> ТЗ.

Мы будем рассматривать только такие задачи поиска, в которых в ответ на запрос надо перечислить элементы базы данных, удовлетворяющие запросу. ЗИП такого типа называются задачами на перечисление. С учетом этого факта мы и дадим собственную формализацию ЗИП, более удобную для использования в дальнейшем.

Из приведенных примеров видно, что в задачах поиска имеется некий универсум, из которого берутся объекты поиска (элементы базы данных). В первом примере таким универсумом является множество всевозможных ключей, а во втором — отрезок [0,1] вещественной прямой. Этот универсум обозначим через У и будем называть множеством объектов поиска или множеством записей, а элементы множества У, будем называть, записями.

Далее в задачах поиска всегда имеется множество запросов. В первом примере множество запросов совпадает с множеством объектов поиска и является множеством всевозможных ключей, а во втором примере множество запросов есть множество всех отрезков, содержащихся в [0,1], т. е. множество {(u, v): 0 ^ и ^ v ^ 1}. Множество запросов будем обозначать через X.

На декартовом произведении X х У имеется бинарное отношение, которое позволяет устанавливать, когда запись из У удовлетворяет запросу из X. Это отношение будем называть отношением поиска. В первом примере отношение поиска есть отношение идентичности (равенства), т. е. запись удовлетворяет запросу, если они идентичны. Во втором примере отношение поиска, которое обозначим через pint, определяется соотношением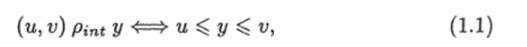

где (и, v) € Х_у у е У Тройку S = {X, У, р), где X — множество запросов, У — множество записей, р — отношение поиска, заданное на X х У, будем называть типом или иногда более развернуто типом задан информационного поиска.

Тройку I = (X, У, р), где X — множество запросов; V — некоторое конечное подмножество множества У, в дальнейшем называемое библиотекой-, р — отношение поиска, заданное на X х У, будем называть задачей информационного поиска (ЗИП) типа S — (Х, У, р). Содержательно будем считать, что задача I = (X, V, р) состоит в перечислении для произвольно взятого запроса х € X всех тех и только тех записей из V, которые находятся в отношении р с запросом х, т. е. удовлетворяют запросу х.

Тем самым, мы формализовали понятие ЗИП.

Для полной определенности отмстим, что поскольку библиотека V есть множество, то в ней все элементы различные, т. е. в ней нет повторяющихся элементов.

Относительно терминологии: если заменить термин «запись» на термин «документ», то получившаяся терминология полностью будет согласовываться с терминологией, принятой в теории информационного поиска [103]. Произведенная замена сделала в связи с тем, что под термином «документ» в теории информационного поиска понимается любой записанный на материальном носителе осмысленный текст, который обладает определенной логической завершенностью. Более подходящий термин «поисковый образ», под которым понимают текст, который выражает на используемом поисковом языке центральную тему или предмет документа, тоже не совсем удовлетворителен, поскольку под «записью» понимается скорее поле документа, по которому производится поиск. Поэтому мы остановились на термине «запись» как на более нейтральном и в других пониманиях не используемом.

Следующий шаг, который мы обязаны сделать, — это выбрать математическую модель для алгоритмов поиска.

Отметим, что здесь и всюду далее, используя термин «алгоритм», мы часто будем подменять им понятие «условного алгоритма» (или «относительного алгоритма», см. [66, с. 44−45]), т. е. будем рассматривать алгоритмы, которые выполняются при условии, что мы умеем выполнять некоторые операции из описанного заранее множества. В качестве таких операций могут выступать, например, некоторые операции над вещественными числами, но так или иначе мы всегда будем явно оговаривать операции, относительно которых рассматривается каждый описываемый условный алгоритм.

Переберем возможных кандидатов на роль математической модели для алгоритмов поиска.

• 1) Алгоритмы поиска информации можно описывать на языке программирования, например на Си++ [96]. Положительным фактором такого подхода является то, что любое описание алгоритма одновременно будет и его реализацией. Отрицательным — то, что помимо описания алгоритма нам понадобится по алгоритму определять его сложность, а в этом случае это сделать весьма трудно, более того неясно, как сделать этот переход формально. Как следствие, мы не можем использовать этот язык для получения нижних оценок сложности алгоритмов.
• 2) Алгоритмы поиска можно описывать с помощью машин Тьюринга (63, 107, 209]. Если под сложностью алгоритма понимать время поиска, этот подход обладает тем же недостатком, что и первый, но плюс к этому добавляется трудность программирования для машин Тьюринга.
• 3) Для описания алгоритмов поиска можно использовать схемы алгоритмов Янова |51, 109] или стандартные схемы программ Котова [61]. Неудобство использования этих схем определяется тем, что они предназначены для других целей, а именно для исследования проблемы эквивалентности алгоритмов. Поэтому если мы даже сможем адаптировать эти понятия для наших нужд, то пропадает главное преимущество, которое дает использование известных моделей — это наработанный аппарат.
• 4) Необходимо вспомнить алгебраическую модель информационного поиска, разработанную В. Н. Решетниковым (11, 87−91]. В этих работах некоторая задача поиска, возникающая в дсскрипторных автоматизированных информационно-поисковых системах [2, 103, 106] (по сути это разновидность поиска по ключевым словам), сводится к решению системы линейных уравнений и неравенств на конечном множестве линейного пространства над конечным полем коэффициентов, а точнее над полем характеристики 2, т. е. булевым кубом. По утверждению В. Н. Решетникова [87] алгебраическая модель позволяет ставить и решать различные задачи оптимизации, например, алгебраическая теория информационного поиска позволяет перенести на этот класс задач методы регуляризации (работа В. Н. Решетникова велась на факультете ВМиК МГУ). Но поскольку из работ В. Н. Решетникова выясняется, что нет эффективных методов решения упомянутых систем линейных уравнений и неравенств, то алгебраическая модель практически ничего не дала в плане создания эффективных алгоритмов поиска, а предложенная В. Н. Решетниковым Z-структура [90, 91] по сути является сбалансированным деревом поиска, и единственное, что о ней сказано — что в некоторых случаях алгоритм, использующий Z-структуру эффективней перебора.
• 5) В качестве модели вычислений можно использовать машину с произвольным доступом к памяти, аналогичную описанной в [10] с добавлением возможности выполнения арифметических операций над действительными числами. Это значит, что в такой машине каждая ячейка памяти может содержать действительное число, а каждая арифметическая операция, такая, как сложение, умножение и деление, может быть выполнена за единицу времени. В зависимости от решаемой задачи машина может иметь некоторые другие примитивные операции, о которых предполагается, что они выполняются за постоянное время.

Известной моделью, используемой для исследования сложности алгоритмов, является алгебраическое дерево вычислений [112, 142, 194, 195].

Пусть К — множество действительных чисел. Алгебраическое дерево вычислений (АДВ) [112, Бен-Op] на множестве переменных W = = {xi, X2,…, x_n}, ^гД^е € К есть бинарное дерево D, размеченное следующим образом:

1. Каждой вершине v, имеющей в точности одного сына (простая вершина), приписывается операция вида f_v := # f_V2 или.

fv fv #c или f_v := где v, (i = 1,2) — предок вершины v

в дереве D, или f_Vi 6 W, # E {+, —, x,/}, ac 6 R является константой.

2. Каждой вершине t>, имеющей в точности двух сыновей (вершина ветвления), приписывается операция сравнения вида f_Vl > 0 или f_Vl < 0 или f_Vl = 0, где Vi — предок вершины v в дереве D, или Л" € W.

3. Каждому листу дерева приписывается одно из значений ДА или НЕТ.

Приведем пример использования АДВ для задачи поиска идентичных объектов I = (X, V, =) в случае, когда множества запросов X = [0,1] С R и V С [0,1]. Для каждого заданного запроса х G X программа прокладывает в дереве D путь Р (ж), начинающийся в корне. При прохождении каждой простой вершины выполняется арифметическая операция, приписанная этой вершине, а в каждой вершине ветвления происходит ветвление в соответствии с результатом сравнения, приписанного вершине. При достижении листа дерева возвращается ответ ДА или НЕТ. Считается, что АДВ D решает задачу /, если возвращаемый ответ верен для любого запроса х? X. Сложность дерева ?>, обозначаемая C (D), определяется как максимум величины cost (x, D) по всем значениям х, где cost (x, D) — число вершин, проходимых путем Р (х) в дереве D. Сложность задачи /, обозначаемая С (/), есть минимум C (D) по всем алгебраическим деревьям вычислений Z7, решающих задачу I.

Разновидностью алгебраического дерева вычислений является так называемое (алгебраическое) дерево решений порядка d [207]. Дерево решений порядка d — это дерево, каждой вершине которого соответствует сравнение вида /(х) 7 0, где / имеет полиномиальную сложность относительно входных данных с показателем степени не более d и 7 € {>,<,=}. В случае, когда d равно 1, получается линейное дерево решений, с использованием которого получены доказательства ряда нижних оценок сложности [140−142, 195, 213, 215]. Серьезные исследования временной сложности алгебраических деревьев решений проводились М. Ю. Мошковым [72−77].

В чем заключаются недостатки использования алгебраического дерева вычислений Бен-Ора или алгебраического дерева решений порядка d для моделирования алгоритмов поиска? Во-первых, хотелось бы более полно учитывать специфику алгоритмов поиска. Вовторых, использование алгебраического дерева вычислений Бен-Ора или алгебраического дерева решений порядка d приводит к некоторым заблуждениям. Так в рамках АДВ (так же как и в рамках линейного дерева решений) задача поиска идентичных объектов I = (Х_: V, =) в случае, когда множества запросов X = [0,1] С К и V С [0,1], имеет нижнюю оценку сложности 0(log₂ п), где п — число точек в библиотеке V. Это так называемая теоретико-информационная оценка [121]. Понятно откуда получается эта оценка — бинарное дерево с п листьями должно иметь высоту как минимум log₂ п. Сила влияния этой оценки настолько велика и заблуждение о неизбежности такого времени для решения настолько глубоко, что часто алгоритмы с оценкой 0(log₂ п) называют оптимальными. Тогда как эта оценка всего лишь следствие бинарности дерева решений, и если отказаться от бинарности, то не будет и оценки. С помощью этой оценки получается нижняя оценка сложности порядка 0(nlog₂n) для задачи сортировки множества из п элементов [10]. На основе оценки сложности сортировки с помощью метода сведения одной задачи к другой [204] можно показать, что большое количество задач требуют для своего решения время 0(nlog₂n) в рамках АДВ-модели вычислений [123, 142, 148, 180, 185, 193, 195, 200, 203−207, 211, 214] в том числе задача построения выпуклой оболочки п точек на плоскости, задача построения евклидова минимального остовного дерева и т. д.

Но если отказаться от АДВ-модели вычислений, то для нашей задачи поиска идентичных объектов I = (X, У, =) легко предложить алгоритм, который решает эту задачу за константное время, при условии, что можно осуществлять предобработку и использовать дополнительную память. Пусть У = {j/i,…, j/_n} — упорядоченное по возрастанию множество точек. Найдем расстояние между двумя ближайшими точками. Пусть оно равно d. Поделим отрезок (0,1] на т = ]1 /d[ равных частей, так что t-ая часть (* = 0, m — 1) имеет вид (i/m, (t + 1 )/тп. Тогда в каждую часть попадет не более одной точки из У. Заведем целочисленный массив А длины т, г-ый элемент которого (г = 0, т—1) содержит 0, если в г-ой части нет точек из У, и номер j, если в г-ую часть попала точка yj из У. После такой предобработки поиск по произвольному запросу х 6 (0,1) будем осуществлять следующим образом. Вычислим j = [х • т]. Номер j дает номер части, в которую попала точка х. Если Aj = 0, то точки х в библиотеке У нет, иначе сравниваем y_yj с х и если они равны, то точка х найдена.

Мы откажемся от использования АДВ-модели, в частности, чтобы не быть зажатыми теоретико-информационной оценкой [121].

6) Прежде чем предложить еще одну модель алгоритмов поиска взглянем на алгоритм, решающий задачу поиска с функциональной точки зрения.

Рассмотрим произвольную ЗИП I = (X, V, р). Алгоритм поиска решает ЗИП, если на любой запрос из множества запросов X он выдает все те и только те записи из У, которые удовлетворяют запросу. Возьмем произвольную запись у € Y. Для нее можно ввести характеристическую функцию

т. е. она равна 1 на тех запросах, которым удовлетворяет запись у. Тогда можно сказать, что алгоритм, решающий ЗИП I = (X, У, р), где У = {2/1,…, 2/к}, *— ни что иное как алгоритм, реализующий систему функций {xyi, р> • • • >Ху*, р}- Следовательно, управляющая система, моделирующая алгоритм, решающий ЗИП I = (X, У, р), должна представлять собой многополюсник, реализующий множество характеристических функций {Хуьр> • • • >Ху*, р};

Рассмотрим случай когда множество запросов X = В^п — п- мерный единичный куб. Тогда каждая из функций Хуг, р будет функцией алгебры логики и, значит, в классе контактных схем [65] можно построить многополюсник, реализующий множество функций {Хуьрэ • • •"Ху*, Л как функций проводимости.

Если множество запросов не является n-мерным единичным кубом, то можно вместо множества {хь…, х", Xi,…, х"} использовать для нагрузки ребер некоторое множество F предикатов, определенных на множестве запросов X. Тогда при удачном выборе множества F и правильной нагрузке ребер многополюсника предикатами из F мы можем в качестве функций проводимости между полюсами получить характеристические функции Xy_itp (* ⁼⁼ 1>Л). Но если вводить сложность полученной многополюсной сети так же как в контактных схемах (т. е. как количество ребер сети), то эта сложность скорее будет характеризовать объем памяти, соответствующего алгоритма, но не время поиска. Чтобы сложность сети характеризовала время поиска, ее надо вводить на подобии того, как это делалось в АДВмодели. Для этого будем считать, что сеть у нас ориентированная, что в сети есть такой полюс, который называется корнем, и каждая из характеристических функций записей Xy_itp (* = 1"&) реализуется как функция проводимости между корнем и своим полюсом, который отметим приписыванием ему записи у*. Теперь если взять произвольный запрос х € X, то алгоритм функционирования сети на запросе х можно описать аналогично алгоритму разметки графа [51, 61]: считаем, что в начальный момент все вершины сети, кроме корня, неотмеченные, а некоторое упорядоченное множество вершин сети, которое назовем множеством активных вершин, содержит только корень сети. На каждом очередном шаге делаем следующее. Если множество активных вершин не пусто, то выбираем первую активную вершину и удаляем ее из множества активных вершин. Если выбранная вершина является полюсом, то соответствующую ей запись включаем в ответ на запрос х. Просматриваем в некотором порядке все ребра, исходящие из выбранной вершины, и если предикат, приписанный просматриваемому ребру, на запросе х принимает значение 1 и конец просматриваемого ребра — неотмеченная вершина, то отмечаем конец просматриваемого ребра и включаем его в множество активных вершин (если мы включим его в начало множества активных вершин, то получим алгоритм обхода «сначала вглубь», а если в конец — то «сначала вширь»). Алгоритм завершает работу в тот момент, когда множество активных вершин окажется пустым.

Легко видеть, что если между корнем сети и некоторой вершиной на запросе х есть проводимость, т. е. из корня в эту вершину ведет некоторая цепочка ребер, каждому из которых приписан предикат, принимающий значение 1 на запросе х, то обязательно в результате описанного алгоритма обхода сети данная вершина окажется отмеченной, т. е. алгоритм обхода посетит ее.

Описанный алгоритм обхода сети можно считать соответствующим сети алгоритмом поиска на запросе х, а сложность сети на запросе х можно считать равной, как и в АДВ-модели, числу просмотренных ребер, или, что-то же самое, числу вычисленных алгоритмом обхода предикатов. Такая сложность будет характеризовать время работы соответствующего алгоритма поиска на запросе х.

Описанную сеть с описанным функционированием будем называть предикатным информационным графом. Необходимо отметить, что ранее, в том числе практически во всех статьях одного из авторов, этот объект носил название информационной сети. Но этот термин столь часто создавал ненужную путаницу, вызывая ассоциацию с сетями передачи информации, что пришлось принять решение о замене термина.

Предикатный информационный граф можно рассматривать как обобщение контактных схем и АДВ-модели, причем от контактных схем заимствована структура в виде сети с нагрузкой ребер функциями и использование функций проводимости, а от АДВ-модели — способ введения сложности сети. Кроме того, вводится алгоритм обхода сети, похожий на алгоритм разметки графа (51, 61], который можно рассматривать как соответствующий сети алгоритм поиска. Причем в каждой вершине сети, до которой на некотором запросе х дошел алгоритм поиска, каждое из ребер, исходящее из этой вершины, задает возможное направление поиска, и если на этом запросе х значение предиката, соответствующего ребру, равно 1, то в направлении данного ребра поиск продолжается, а если равно 0, то по этому направлению поиск прекращается. Таким образом, из одной вершины сети может возникнуть сразу несколько направлений, по которым поиск продолжается. Но в задачах поиска часто встречается ситуация, когда из нескольких направлений поиска выбирается точно одно, например, так как это происходит в вершине ветвления алгебраического дерева вычислений, когда в зависимости от результата сравнения выбирается одно из двух направлений движения. В таких случаях гораздо удобнее приписать вершине функцию-переключатель и в зависимости от ее значения на запросе выбрать то направление, на которое указывает значение переключателя. Поэтому слегка усложним понятие предикатного информационного графа. Для этого введем множество G переключателей, т. е. функций, определенных на множестве запросов X и принимающих значения из конечного подмножества натурального ряда. Теперь если дана ненагруженная многополюсная ориентированная сеть, то нагрузку сети функциями будем осуществлять следующим образом. Сначала выберем в сети некоторое количество вершин, которые назовем точками переключения, и каждой точке переключения припишем некоторый переключатель из G и затем занумеруем подряд, начиная с 1, ребра, исходящие из нее. Такие ребра, исходящие из точек переключения, назовем переключательными. Остальные ребра назовем предикатными и нагрузим их предикатами из множества F. Нагрузим все полюсы сети, кроме корня, записями, причем можем считать, что одна и та же запись может быть приписана нескольким полюсам. Алгоритм обхода сети на запросе в этом случае полностью аналогичен описанному ранее за тем исключением, что если активная выбранная вершина является точкой переключения, то вычисляем значение переключателя, соответствующего вершине, на запросе т, и если среди ребер, исходящих из этой вершины, есть ребро с номером, равным вычисленному значению, то включаем конец этого ребра в множество активных вершин, если только этот конец не был отмеченной вершиной. Полученную нагруженную сеть с описанным функционированием будем называть информационным графом (ИГ).

Прежде чем дать строгое формальное определение ИГ, введем некоторые вспомогательные понятия и обозначения.

Пусть М —- некоторое конечное множество. Через М обозначим число элементов во множестве М, называемое мощностью множества М. _.

Через {1,771} договоримся обозначать множество {1,2, т}.

Некоторые оценки мы будем приводить с точностью до главного члена, поэтому введем обозначения, обычно принятые при описании асимптотических оценок.

Будем писать а (п) = о (1), если lim а (п) = 0; А (п) = б (?(п)), если.

п—>со

А (п) = В (п)-о (1). Скажем, что А (п) асимптотически не превосходит В (п) при п —У оо и обозначим А <. В, если существует а (п) = о (1) такое, что начиная с некоторого номера no, А (п) ^ (1 + а (п)) • В (п). Если А < В и В <, А, то будем говорить, что Ап В асимптотически равны при п —> оо и обозначать А ~ В. Будем писать А % В, если существует такая положительная константа с, что А (п) ^ с • В (п), начиная с некоторого номера щ. Если А ^ В и В ^ А, то будем говорить, что А п В равны по порядку при п —" оо и обозначать А ж В или А — 0(B).

Через (?) будем обозначать число сочетаний из п элементов по к. Если г — действительное число, то через [г] будем обозначать максимальное целое, не превышающее г, а через ]г[ — минимальное целое, не меньшее, чем г. Значок ^d=^f будем понимать как «по определению равно». Математическое ожидание будем обозначать значком М, а значок М_х будем понимать как среднее значение при вариации переменной х.

Договоримся также о теоретико-графовой терминологии.

Пусть нам дан ориентированный граф. В ориентированном ребре (а,/?) вершину а будем называть началом ребра, а @ — концом. Скажем, что ориентированное ребро графа исходит из вершины Р (входит в вершину Р), если р — начало (конец) данного ребра. Скажем, что ребро инцидентно вершине, если эта вершина является одним из концов данного ребра. Полу степенью исхода (захода) вершины графа назовем число ребер, исходящих из данной вершины (входящих в данную вершину). Степенью инцидентности вершины назовем число инцидентных ей ребер. Вершину графа назовем концевой, если полустепень ее исхода равна 0. Остальные вершины графа назовем внутренними.

Последовательность ориентированных ребер графа.

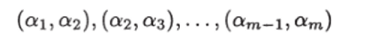
назовем ориентированной цепью от вершины ai к вершине а_т.

Если / — одноместный предикат, определенный на X, т. е. /: X —> —> {0,1}, то множество N/ = {х € X: f (x) = 1} назовем характеристическим множеством предиката /.

Множество 0(у, р) = {х € X: х р у} назовем тенью записи у 6 Y.

Функцию Ху, р^: X -> {0,1} такую, что N_Xvp = 0(у,/?), назовем характеристической функцией записи у.

В формальном определении понятия ИГ используются четыре множества:

• • множество запросов Х
• • множество записей У;
• • множество F одноместных предикатов, заданных на множестве Х
• • множество G одноместных переключателей, заданных на множестве X (переключатели — это функции, область значений которых является начальным отрезком натурального ряда).

Пару Т = (F, G) будем называть базовым множеством.

Определение понятия ИГ разбивается на два шага. На первом шаге раскрывается структурная (схемная) часть этого понятия, на втором — функциональная.

Определение ИГ с точки зрения его структуры.

Пусть нам дана ориентированная многополюсная сеть.

Выделим в ней один полюс и назовем его корнем, а остальные полюсы назовем листьями.

Выделим в сети некоторые вершины и назовем их точками переключения (полюсы могут быть точками переключения).

Если 0 — вершина сети, то через фр обозначим полустепень исхода вершины 0.

Каждой точке переключения 0 сопоставим некий символ из G. Это соответствие назовем нагрузкой точек переключения.

Для каждой точки переключения 0 ребрам, из нее исходящим, поставим во взаимно однозначное соответствие числа из множества {1, фр}. Эти ребра назовем переключательными, а это соответствие — нагрузкой переключательных ребер. Ребра, не являющиеся переключательными, назовем предикатными.

Каждому предикатному ребру сети сопоставим некоторый символ из множества F. Это соответствие назовем нагрузкой предикатных ребер.

Сопоставим каждому листу сети некоторую запись из множества У. Это соответствие назовем нагрузкой листьев.

Полученную нагруженную сеть назовем информационным графом над базовым множеством Т = (F>G).

Определение функционирования ИГ.

Скажем, что предикатное ребро проводит запрос х € X, если предикат, приписанный этому ребру, принимает значение 1 на запросе х; переключательное ребро, которому приписан номер п, проводит запрос х € X, если переключатель, приписанный началу этого ребра, принимает значение п на запросе х; ориентированная цепочка ребер проводит запрос х? X, если каждое ребро цепочки проводит запрос х; запрос х? X проходит в вершину 0 ИГ, если существует ориентированная цепочка, ведущая из корня в вершину /3, которая проводит запрос х; запись у, приписанная листу а, попадает в ответ ИГ на запрос х? X, если запрос х проходит в лист а. Ответом ИГ U па запрос х назовем множество записей, попавших в ответ ИГ на запрос х, и обозначим его Ju (x). Эту функцию Ju (x) X —> 2^У будем считать результатом функционирования ИГ U и называть функцией ответа ИГ U.

Понятие ИГ полностью определено.

Проиллюстрируем приведенное определение на примере одномерной задачи интервального поиска. В этом случае 4 множества, определяющие ИГ, имеют вид:

• • множество запросов X_tn* = {(ц, ц): 0 ^ и ^ v ^ 1};
• • множество записей Уш = [0,1];
• • множество предикатов F = F (J F2, где

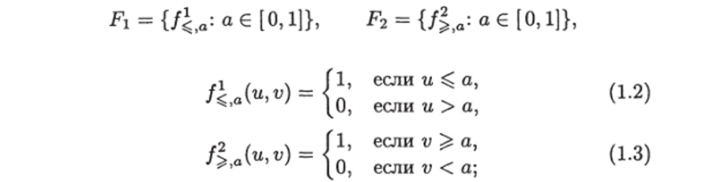
• множество переключателей G = G U G2 U G3, где.

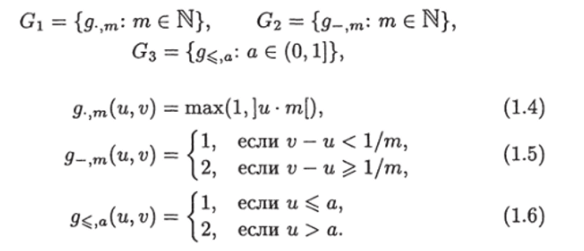
В информационном графе, приведенном на рис. 1.1, корень изображен полым кружком. Листья изображены жирными точками, а записи, приписанные листьям, — это символы у с индексами. На рисунке имеется 8 переключательных вершин (им приписаны символы д с индексами) и 17 предикатных ребра (им приписаны символы / с индексами).

Если п — натуральное число, а у (х) — некий переключатель, то через ?? (х) обозначим предикат, определенный на X, такой что.

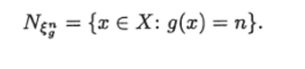
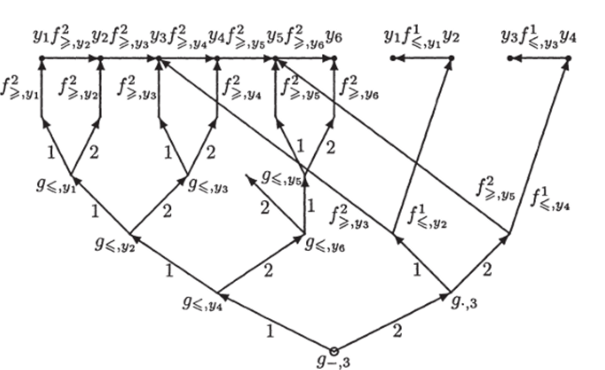
Рис. 1.1. Решение одномерной задачи интервального поиска.

Обозначим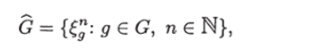

где N — множество натуральных чисел.

Если с — ребро ИГ, то через [с] обозначим его нагрузку.

В соответствии с приведенными выше определениями введем функции проводимости.

Проводимостью ребра (a, р) назовем предикат, равный [(а,/?)], если ребро предикатное, и ^а', если ребро переключательное, где g — переключатель, соответствующий вершине а.

Проводимостью ориентированной цепи назовем конъюнкцию проводимостей ребер цепи.

Если зафиксировать запрос я, то цепь, проводимость которой на запросе я равна 1, назовем проводящей цепью на запросе х.

В ИГ по аналогии с контактными схемами введем для каждой пары вершин а и (3 функцию проводимости f_Qp от вершины, а к вершине Р следующим образом:

• • если а = р, то f_ap{x) = 1 (х € Х)
• • если а ф Р и в ИГ не существует ориентированных цепей от, а к Ру то /_ар (х) ЕЕ 0;
• • если ос ф Р и множество ориентированных цепей от, а к р не пусто, то }_Q0(x) равно дизъюнкции проводимостей всех ориентированных цепей от, а к Р.

Функцию проводимости от корня ИГ к некоторой вершине Р ИГ назовем функцией фильтра вершины р и обозначим <�рр (х).

Через 7Z (U), V (IJ)>C (U) (или просто 7?, Р, С) обозначим множества вершин, точек переключения и листьев ИГ U соответственно.

Пусть ЛГ — некоторая подсеть (т. е. произвольное подмножество вершин и ребер) ИГ U. Через (Л/) обозначим множество записей, соответствующих листьям этой подсети (если а — некоторый лист ИГ U, то под (а) будем понимать запись, соответствующую листу от).

Легко видеть, что функция ответа ИГ U определяется соотношением.

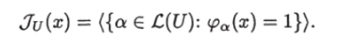
Из определения функционирования ИГ видно, что ИГ как управляющая система может рассматриваться в качестве модели алгоритма поиска, работающего над данными, организованными в структуру, определяемую структурой ИГ.

Достоинства ИГ:

• 1) все основные известные ранее объекты, используемые для моделирования алгоритмов поиска, являются частными случаями ИГ;
• 2) все наиболее популярные и известные алгоритмы поиска легко перекладываются на язык ИГ и при этом приобретают свойство метризуемости, т. е. становится легко подсчитать такие характеристики сложности алгоритмов как объем памяти, время поиска в среднем и время поиска в худшем случае, причем полученные с помощью ИГ оценки полностью согласуются с оценками, полученными другими методами, если такие оценки существовали.

Подтверждение сказанного:

• 1) Наиболее популярная модель, используемая для оценки сложности алгоритмов, — алгебраическое дерево вычислений (АДВ-модель), а также ее разновидность — алгебраическое дерево решений, при переводе на язык ИГ описываются некоторым классом древовидных ИГ и, тем самым, являются частным случаем ИГ.
• 2) Алгоритмы и конструкции, используемые в древовидных и лингвистических базах данных, описываются древовидными ИГ.
• 3) Алгоритм поиска, используемый в дедуктивных базах данных, при переходе на язык ИГ приводит к константному дереву.
• 4) Алгоритмы в реляционных базах данных приводят к древовидным ИГ специального вида.

В случае, когда базовое множество переключателей G пусто, т. е. в графах нет переключателей, то ИГ называются предикатными информационными графами (ПИГ). Ранее этот термин носил название информационных сетей с дублированием листьев (ИСД). Понятие ПИГ хронологически предшествовало понятию ИГ и впервые эти понятия были опубликованы в [23].

ПИГ, различным листьям которого соответствуют различные заг писи, называется однозначным информационным графом (ОИГ). Это понятие (под названием «информационная сеть») впервые введено в [20]. Более доступными изданиями являются [21, 22].

ОИГ, имеющий вид дерева, листья которого совпадают с концевыми вершинами дерева, назовем информационным деревом (ИД).

Впервые понятие ИД было опубликовано в работах [14−18, 153].

ИД удобны и интересны тем, что структуры данных, им соответствующие, практичны и их гораздо проще реализовать на ЭВМ.

Приведем пример еще одного ИГ. Пусть I = {Х_у V_t =) — задача поиска идентичных объектов, где на множестве V = {г/i,…, у7} задан линейный порядок и записи упорядочены в порядке возраста ия, т. е. 2/1 ^2/1 ^ * * * ^ 2/7- Пусть множество предикатов имеет вид.

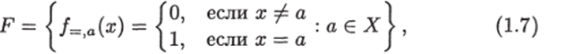
а множество переключателей — вид.

Бинарным поиском или методом деления пополам (см., например, [10, 56, 68]) называется алгоритм поиска в упорядоченном массиве, при котором массив делится пополам, запрос сравнивается со средней точкой и в зависимости от результата сравнения поиск рекурсивно повторяется в одной из половин.

На рис. 1.2 приведен ИГ над базовым множеством Т = (F, G), решающий ЗИП /, соответствующий бинарному поиску в версии Боттенбрука [122, с. 214], в которой вопрос о равенстве записи и запроса откладывается до самого последнего момента.

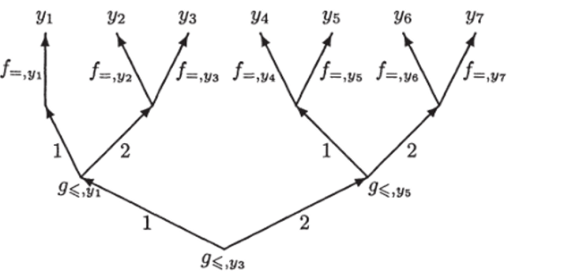
Рис. 1.2. Информационный граф бинарного поиска.

Введение

управляющей системы, т. е. схемы с функционированием, для моделирования алгоритмов поиска позволяет использовать аппарат теории сложности управляющих систем для исследования сложности алгоритмов поиска.

Упражнения.

• 1.1. По аналогии с одномерной задачей интервального поиска приведите тип, описывающий n-мерные задачи интервального поиска.
• 1.2. Опишите тип, задающий задачи интервального поиска на пмерном булевом кубе, которые состоят в поиске в конечном подмножестве п-мерного булевого куба всех тех точек, которые попадают в подкуб, задаваемый запросом. Какова мощность множества запросов у данного типа?
• 1.3. Задача о метрической близости состоит в том, чтобы по произвольно взятой точке-запросу единичного n-мерного куба п-мерного евклидового пространства найти в конечном подмножестве этого куба (библиотеке) все точки, находящиеся на расстоянии не более, чем R от точки запроса. Опишите тип, задающий задачи о метрической близости.
• 1.4. Опишите тип, задающий задачи включающего поиска. Напомним, что в задаче включающего поиска имеется некоторое конечное множество свойств, и каждый элемент библиотеки (множества данных) обладает или не обладает каждым из этих свойств. Запрос задает некоторое подмножество множества свойств, и необходимо найти все элементы библиотеки, которые обладают всеми свойствами из запроса.
• 1.5. Рассмотрим следующую задачу поиска, которая может возникнуть, например, при разгадывании кроссвордов. Элементы библиотеки (записи) есть слова фиксированной длины п в алфавите {0,1}. Запрос задает некоторый набор позиций и значения букв в этих позициях. Необходимо найти в библиотеке все записи, у которых в позициях, задаваемых запросом, стоят буквы, совпадающие с соответствующими значениями позиций запроса. Опишите тип, задающий эти задачи поиска. Сравните полученный тип с типом задач интервального поиска на булевом кубе (см. упражнение 1.2).