Расчет арок с помощью линий влияния

Как было показано при расчете балок, с помощью линий влияния могут быть определены реакции и внутренние усилия не только от временной подвижной, но и от любых статических нагрузок.

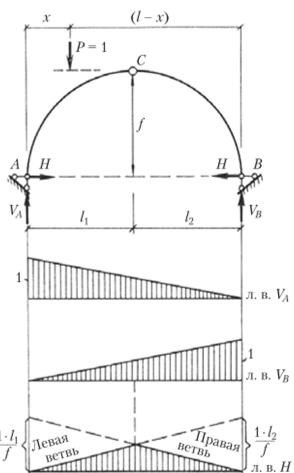
1. Линии влияния опорных реакций. Линии влияния вертикальных составляющих опорных реакций V_A и V_K ничем не отличаются от линий влияния вертикальных реакций простой балки того же пролета.

Согласно рис. 4.15 имеем.

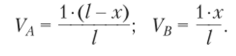
Линия влияния распора будет иметь две ветви при положении груза на левой и правой полуарках.

При положении груза Р = 1 на правой полуарке получим.

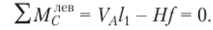
Для левой опоры V_A = 1,.

Для случая, когда груз расположен на левой полуарке, будем иметь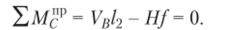

Для правой опоры V_B = 1,.

Выражение (4.8) позволяет провести правую ветвь, а выражение (4.9) — левую (см. рис. 4.15).

2. Линия влияния изгибающего момента строится исходя из основного выражения для момента в каком-либо заданном сечении М_т = М® — Ну_т и является результатом сложения двух линий влияния: линии влияния момента М® в сечении т простой балки такого же пролета и линии влияния распора Н с умножением всех его ординат на у_т. Для этого две указанные линии влияния строятся на одном рисунке, что приведет к их суммированию (с учетом знаков). Ординаты, заштрихованные между двумя линиями, будут равны ординатам искомого момента, как показано на рис. 4.16.

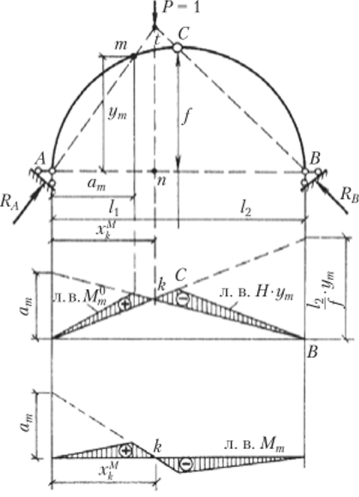
Рис. 4.16.

Обычно линии влияния моментов строятся в виде графика на горизонтальном базисе, как показано на рис. 4.16. Для этой линии влияния необходимо найти абсциссу нулевой точки xjf. Нулевая точка соответствует положению подвижного груза Р = 1, от действия которого изгибающий момент в сечении, проходящем через точку т, равен нулю. Используем условия равновесия каждой полуарки в отдельности. В этом случае должны соблюдаться следующие условия:

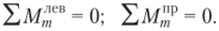
Для соблюдения первого условия, когда на участке А—т (см. рис. 4.16) не действуют внешние силы, линия действия реакции R_A должна проходить через точку т, а для соблюдения второго условия, когда па полуарку ВС не действуют внешние силы, линия действия реакции R_B должна проходить через шарнир С. В таком случае из условия равновесия трех сил груз Р — 1 должен находиться в точке пересечения указанных направлений реакций, что соответствует положению нулевой точки k.

Из полученного построения нетрудно вывести и аналитическое выражение для абсциссы х

Рассматривая треугольники Atn и Btn, можем записать.

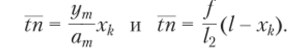
Приравнивая оба выражения, получим.

3. Линия влияния поперечной силы также строится исходя из общего выражения.

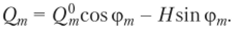
Так как для заданного сечения m угол наклона касательной известен, то легко определяются и тригонометрические функции. Линия влияния строится способом наложения двух линий влияния: л. в. балочной поперечной силы Q®_n ординаты которой умножены на cos (p_w, и л. в. распора, ординаты которой умножены на sin (p_/w.

Построенная линия влияния показана на рис. 4.17.

Рассуждения по отысканию положения груза Р = 1, соответствующего нулевой поперечной силе в сечении тп, аналогичны тем, которые были даны при построении линии влияния изгибающего момента. При этом надо иметь в виду, что равнодействующая всех левых сил (реакция R_A) до сечения m должна быть направлена параллельно касательной, проведенной в сечении тп. В таком случае равнодействующая R_a не дает составляющей поперечной силы.

Рис. 4.17.

Аналитическое выражение для абсциссы легко получается при рассмотрении треугольников АЬЩ и ЫЩ (см. рис. 4.17) и имеет вид.

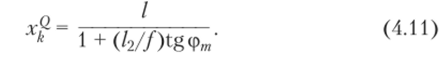
4. Линия влияния продольной силы. Принцип построения л. в. продольной силы N_m тот же, что и л. в. поперечной силы Qrn• Исходим также из общего выражения.

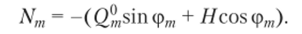
Следует заметить, что при вертикальной нагрузке (подвижный груз Р = 1 и является такой нагрузкой) продольная сила не будет иметь изменения знака ни в одном сечении арки, поэтому использование принципа нулевой точки приводит к тому, что эта точка должна находиться за пределами арки, т. е. является мнимой, так как груз, движущийся в пределах от сечения т до ключевого шарнира С, не может одновременно находиться на линии t₂—n₂ (рис. 4.18).

Общий вид линии влияния показан на рис. 4.18. Рассматривая треугольники At₂n₂ и Bt₂n_2f получим аналитическое выражение для абсциссы нулевой точки k:

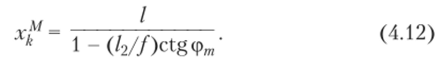
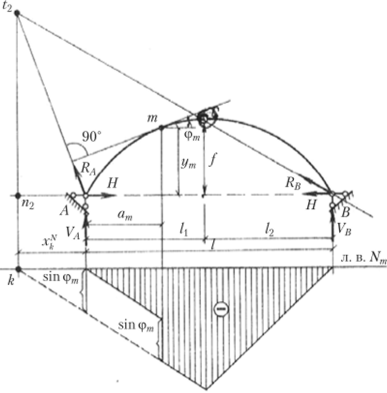
Рис. 4.18.