Система гидромеханических уравнений

полидисперсной многофазной смеси с учетом дробления (измельчения) и смешения частиц дисперсных фаз В рамках математического аспекта качественного анализа структуры процесса измельчения—смешения на первом уровне иерархии физико-механических эффектов рассмотрим достаточно полное обобщенное математическое описание системы, в состав которой входят: полидисперсная смесь т + 1 фаз, из которых первая фаза — несущая (газ или жидкость), а т фаз присутствуют в виде отдельных частиц различных объемов (размеров), принадлежащих т различным по свойствам сыпучим материалам, подвергающимся дроблению (измельчению) и смешению; рабочие органы, под действием которых происходит измельчение и смешение частиц т дисперсных фаз.

В зависимости от способа измельчения и смешения к рабочим органам могут относиться мелющие тела (шары) различных размеров, измельчающие и перемешивающие элементы (лопастные высокооборотные измельчители, вращающиеся била, роторы, мешалки, дезинтеграторные элементы) и пр. При самонзмельчении роль рабочих органов выполняют сами измельчаемые частицы.

Движение системы, состоящей из многофазной смеси и рабочих органов, будем изучать при следующих допущениях [2, 4, 46, 49—531.

• 1. Размер частиц много больше молекулярно-кинетических размеров.
• 2. Расстояния, на которых параметры движения многофазной смеси меняются существенно, много больше размеров самих частиц и расстояний между ними.
• 3. Введем в каждой точке объема, занятого смесью, объемные содержания фаз а_{ и средние плотности р, причем

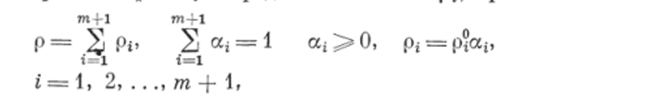
где индекс 1 относится к несущей (первой) фазе, а индексы со 2-го по (т -р 1)-й относятся к т дисперсным фазам измельчаемых и смешиваемых частиц т сортов (сыпучих материалов); р — плотность всей смеси; р*, р? — средняя и истинная плотности i-й составляющей смеси.

• 4. Примем, что частицы в смеси достаточно многочисленны, так что можно считать непрерывным распределение частиц по размерам; тогда полидисперсность i-й фазы частиц характеризуется i-й плотностью распределения числа частиц по объемам /* (г) в единице объема смеси, так что /* (г) dr — число частиц i-й дисперсной фазы в единице объема смеси, объемы которых находятся в пределах от г до г + dr (i = 2, 3,.. т -f 1).
• 5. Плотности р_?— каждой из т дисперсных фаз непрерывно распределены на отрезке [0, /?], где R — объем наибольшей частицы; следовательно, можно записать

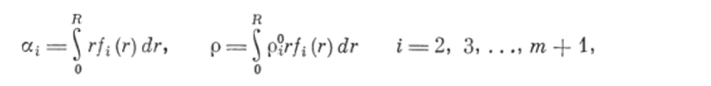
где г — объем частицы.

6. Полагаем, что.

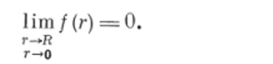
• 7. Разобьем отрезок [0, /?] на N частей и рассмотрим одну из них [г, г Аг]; этой части могут принадлежать частицы всех т дисперсных фаз; совокупность частиц i-й дисперсной фазы во всем объеме измельчающего аппарата, принадлежащих части [г, гfДг], будем называть тч-фазой; в каждой из таких фаз объемы (размеры) частиц остаются постоянными, меняется только их число.
• 8. Первое и второе допущения позволяют описать движение рассматриваемой многофазной смеси в рамках представлений сплошной среды с помощью совокупности взаимопроникающих и взаимодействующих континуумов, заполняющих один и тот же объем (51—53]; на основании этого можно принять, что несущая фаза и все г|-фазы — континуумы, заполняющие один и тот же объем смеси; для каждого из этих континуумов можно определить среднюю плотность Ар* (^r) ⁼⁼ P°i^rfi (^г) Аг, которая представляет собой массу частиц i-й дисперсной фазы (i = 2, 3,.. т + 1) объемами от г до гЬ Дг в единице объема смеси; так же можно определить и другие параметры (скорость, температуру, энергию), относящиеся к своему континууму; если перейдем к пределу при N->? оо, то получим dpi (г) = = p? r/i ®dr, где dpi (г) — масса частиц i-й дисперсной фазы объемами от г до г + dr в единице объема смеси или масса г_гфазы (совокупность частиц i-й дисперсной фазы во всем объеме измельчающего аппарата, принадлежащих отрезку [г, г + с? г]); кроме того, при N -> оо г -> г*.
• 9. Первая фаза является несущей средой, описываемой моделью вязкой жидкости; в качестве тензоров поверхностных сил и тензоров вязких напряжений примем (51, 53]

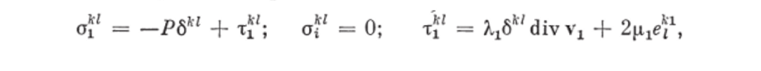
где 6^kl — символ Кронекера; Р — давление; е¹ — тензор скоростей деформаций несущей фазы; v_x — скорость несущей фазы; X_lt щ — коэффициенты вязкости.

10. Предполагаем, что масса, импульс и кинетическая энергия рабочих органов в процессе измельчения—смешения не изменяются (это соответствует отсутствию износа рабочих органов); изменяется только внутренняя энергия рабочих органов за счет совершения работы по измельчению и смешению частиц т дисперсных фаз.

И. Примем гипотезу локального термодинамического равновесия в пределах каждой из фаз, что позволяет ввести для каждой из них свою температуру Г, T_t (г); внутреннюю энергию и_г, u_t (г); энтропию S_x, Si (г) и другие термодинамические функции, а также записать соотношения Гиббса [53, 541 для несущей фазы и г_гфазы.

12. Примем гипотезу локальной однородности фаз; это значит, что^в любом локальном (элементарном) объеме смеси (в пределах рабочего объема измельчающего аппарата) вещество каждой фазы принимается однородным вплоть до поверхности раздела фаз и поэтому энергия и энтропия фазы считаются пропорциональными ее массе; особенности поверхностного слоя вещества толщиной порядка радиуса молекулярного взаимодействия в условиях этой гипотезы учитываться не будут; в рамках принятого предположения энергия и энтропия единицы объема смеси являются аддитивными по массе фаз.

Интегральные уравнения. Выведем интегральные уравнения сохранения массы и импульса для многофазной смеси. Методы механики гетерогенных смесей основаны на физических законах сохранения массы, импульса и энергии. Однако запись уравнений сохранения в общем виде в настоящее время уже не представляет интереса, так как все эти попытки приведут с точностью до обозначений к уравнениям, выведенным в [2, 53). Необходима конкретизация и определение в явном виде величин, описывающих массовое, силовое и энергетическое взаимодействия между фазами. Применительно к процессам массовой кристаллизации из растворов и газовой фазы эта задача успешно решена в работе [511.

Будем записывать балансовые соотношения массы, импульса и энергии для несущей и г_гфазы смеси в некотором (фиксированном в пространстве рабочего объема измельчающего аппарата) объеме смеси Г, ограниченном поверхностью S, учитывая массовое, силовое и энергетическое взаимодействия между фазами за счет физикомеханических эффектов, присущих процессу измельчения—смешения на первом уровне иерархии ФМС. Как мы определили в п. 1.1.1, под локальным будем понимать объем, элементарный по отношению ко всему рабочему объему измельчающего аппарата, но в то же время достаточно большой, чтобы в нем содержалось много частиц всех размеров т дисперсных фаз.

Масса г_гфазы в фиксированном объеме F, ограниченном поверхностью S, определяется выражением.

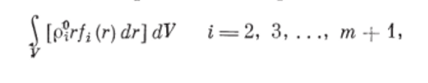
где р? г/^ (г) dr — масса гуфазы в единице объема (см. допущения 4−8).

Скорость изменения массы туфазы описывается производной.

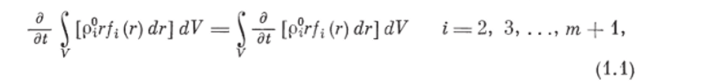
где знак частной производной по времени dldt может быть внесен под знак интеграла, так как операция дифференцирования выполняется при фиксированном в пространстве объеме V.

Изменение массы г_гфазы в объеме V может быть вызвано двумя основными причинами: потоком массы туфазы через поверхность 5, ограничивающую объем У; уменьшением или увеличением массы г_г фазы внутри объема Уза счет действия внутренних стоков или источников (в рассматриваемом случае за счет разрушения частиц объемом от г до г + dr i-и дисперсной фазы и за счет образования частиц объемом от г до г + dr при разрушении всех частиц больших объемов от г до У?).

Аналитическим выражением первой причины является поток вектора Ip? r/f (г) dr] Vj (г) через поверхность S (полагаем, что втекает массы ггфазы больше, чем вытекает)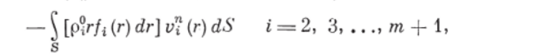

где v_{ (г) — вектор скорости частицы объемом г i-й дисперсной фазы; Vi (г) = V, — (г) п — проекция вектора скорости v*® на внешнюю нормаль п к поверхности S а второй причины — объемные интегралы вида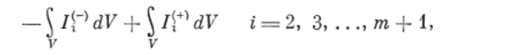

где — уменьшение массы туфазы в единицу времени в единице объема за счет разрушения частиц объемами от г до г + dr i-й дисперсной фазы; /⁽i⁺⁾ — увеличение массы г_гфазы в единицу времени в единице объема за счет образования частиц объемами от г до гf- dr при разрушении всех частиц больших объемов от г до R.

Вследствие этих причин масса гуфазы в объеме V изменяется со скоростью (1.1). Таким образом, получаем баланс массы г_гфазы в объРМА V R кипе.

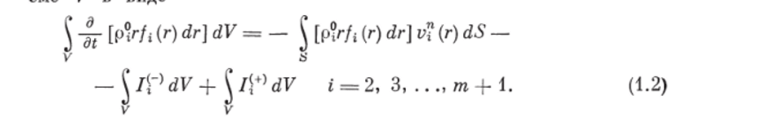
/}-' и в.

явном виде выражения для о.

п р е д е л и м.

/<�Л Измельчение представляет собой случайный процесс разрушения частиц различных объемов в результате механического воздействия рабочих органов. Поэтому для строгого вывода выражений для и /<⁺⁾ прежде всего необходимо определить вероятность разрушения частицы определенного объема в единицу времени.

Обозначим через (г) вероятность разрушения частицы г-й дисперсной фазы объемом г в единицу времени в результате воздействия рабочих органов, а через B_t (rly) — плотность распределения вероятности образования частицы г-й дисперсной фазы объемом г при разрушении частицы объемом у (г < у), причем B_t (rly) dr представляет вероятность образования частицы г-й дисперсной фазы объемом от г до г + dr при разрушении частицы объемом у, а.

Так как измельчение любой частицы происходит в результате взаимодействия (непосредственного контакта) с рабочими органами, то необходимо ввести вероятность столкновения частицы t-й дисперсной фазы объемом г с рабочими органами. Обозначим эту вероятность K_t (г). В зависимости от вида рабочих органов, а значит от способа измельчения и типа измельчающего аппарата, как уже отмечалось в начале данного пункта, вероятность К% (г) будет характеризовать столкновение частицы г-й дисперсной фазы объемом г либо с мелющими телами (шарами), приводимыми в движение центробежными, вибрационными или электромагнитными силами, либо с высокооборотным лопастным измельчителем, вращающимся ротором, мешалкой, либо в случае само измельчения с другими частицами.

В каждый момент времени в объеме V с частицами г-й дисперсной фазы объемами г и у (г <; у)' происходят следующие случайные события:

• 1) столкновение частицы объемом г с рабочими органами (обозначим это случайное событие Е_х);
• 2) разрушение частицы объемом г в результате столкновения •с рабочими органами (случайное событие Е₂);
• 3) столкновение частицы объемом у с рабочими органами (случайное событие Е₃)
• 4) разрушение частицы объемом у в результате столкновения? с рабочими органами (случайное событие Е_А);
• 5) образование частицы объемом г при разрушении частицы объемом у (г < у) (случайное событие Е_ъ).

Из теории вероятностей известно [551, что совмещение нескольких случайных событий, например Е_х П Е_2у есть событие, состоящее в осуществлении и Е_х% и Е₂. В рассматриваемом случае совмещение Е_х П Е₂ — это случайное событие разрушения частицы объемом г г-й дисперсной фазы. Вероятность совмещения этих двух событий Р {Е_х П Е₂) определяет «абсолютную» вероятность разрушения частицы объемом г в единицу впемени [551.

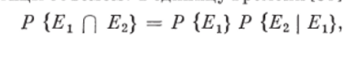
где Р {Е_х} — вероятность осуществления случайного события E_lt т. е. Р {jETj} == Ki (г); Р {Е₂ Е_х} — «условная» вероятность осуществления случайного события Е₂ при осуществлении случайного события Е_г, т. е. Р {Е₂ | Е_г) = (г). Тогда.

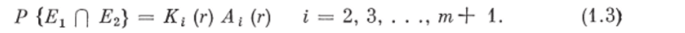
Совмещение случайных событий Е₃ Г) Е₄ П Е_& характеризует случайное событие образования частицы объемом г г-й дисперсной фазы при разрушении частицы объемом у (г < у). Вероятность совмещения этих трех событий Р {Е₃ П Е_х П Е_ь) определяет «абсолютную» вероятность образования частицы объемом г г-й дисперсной фазы при разрушении частицы объемом у (г < у) в единицу времени (551 Р {Ез П Е_л П Е_ь) = Р {Е₃} Р {Е, | Е₃} Р (Е_ъ | Е_л П ^з}, где Р {Е₃} — вероятность осуществления случайного события ?₃, т. е. Р {Е₃) = Ki (у) — вероятность столкновения частицы объемом у i-й дисперсной фазы с рабочими органами; Р {?₄1 ?₃) — «условная» вероятность осуществления случайного события Е₄ при осуществлении случайного события Е₃, т. е. Р {?₄|?₃} = А _{ (у) — вероятность разрушения частицы объемом у г-й дисперсной фазы в единицу времени в результате столкновения с рабочими органами; Р {/?₅ | Е_х П П Е₃} — «условная» вероятность осуществления случайного события Е_ь при одновременном осуществлении случайных событий Е₃ и E_At т. е. Р {Е₆ | Е_а Г) Е₃) = B_t (rly) dr.

Тогда.

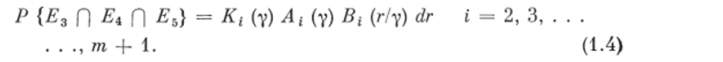
Выражения (1.3) и (1.4) определяют соответственно вероятность разрушения одной частицы объемом г и вероятность образования также одной частицы объемом г при разрушении одной частицы объемом у в результате их столкновений с рабочими органами в единицу времени. Учитывая, что число частиц объемами г и у i-й дисперсной фазы в единице объема равно f_t (г) dr и /* (у) с/у, с помощью (1.3), (1.4) можно найти вероятное число частиц г_гфазы, разрушенных в единицу времени в единице объема: K_t (г) A _t (г) f_t (г) dr и вероятное число частиц г_гфазы, образовавшихся в единицу времени в единице объема в результате разрушения всех частиц i-й дисперсной фазы объемом у: K_t (у) A _t (у) B_t (г/у) f_t (у) dydr.

Иптегрируя последнее выражение по у от г до R, получим вероятное число частиц г_гфазы, образовавшихся в единицу времени в единице объема при разрушении всех частиц объемом от г до R i-й дисперсной фазы:

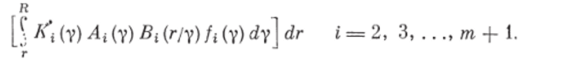
Для упрощения дальнейших выкладок примем, что вероятность столкновения частицы любого объема г-й дисперсной фазы с рабочими органами равна единице, т. е. К₍ (г) = K_t (у) = 1; у, ге ЕЕ [О, /?1. Тогда с учетом того, что масса частицы г_гфазы равна р? г_т получим в явном виде выражения для определения уменьшения и увеличения массы г_гфазы в единицу времени в единице объема:

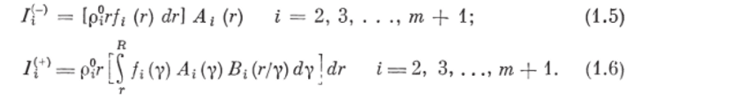
Подставляя выражения (1.5), (1.6) в уравнение (1.2), получим интегральное уравнение сохранения массы г_гфазы внутри объема V в виде.

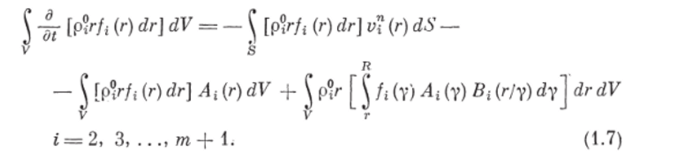
Интегральное уравнение сохранения массы несущей фазы в объеме V, ограниченном поверхностью 5, имеет вид.

где pt — средняя плотность несущей фазы; v™ — проекция вектора скорости на внешнюю нормаль к поверхности S. Интегральное уравнение сохранения импульса несущей фазы можно записать в виде.

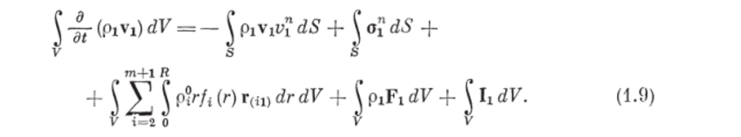
Интегральное уравнение сохранения импульса г_гфазы можно представить в виде.

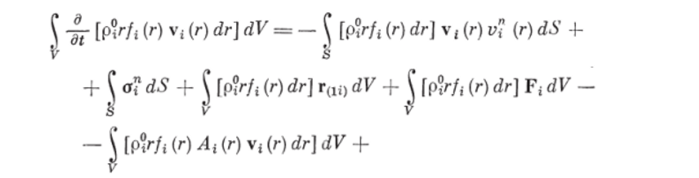
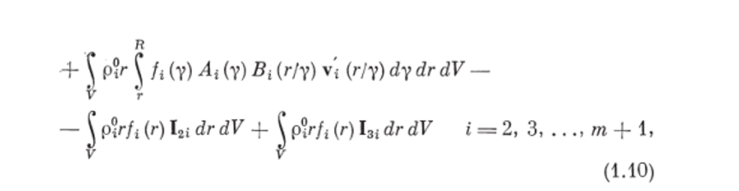
где первые слагаемые в правых частях уравнений (1.9), (1.10) равны притоку импульса соответствующей фазы через поверхность 5; и V, (г) — соответственно скорость несущей фазы и г_гфазы (частиц i-й дисперсной фазы объемом г); v[ (г!у) — скорость частицы объемом г, образовавшейся при разрушении частицы объемом у; вторые, третьи и четвертые слагаемые — это воздействия внешних поверхностных сил, сил взаимодействия между несущей фазой и частицами i-й дисперсной фазы, массовых сил, характеризуемых соответственно тензорами, о*, векторами r_(li), r_(il) и F₂, F*, причем в силу допущения 9 о¹ = 0. Последнее слагаемое в уравнении (1.9) определяет изменение импульса несущей фазы за счет дробления (измельчения) и столкновений частиц всех т дисперсных фаз между собой, не приводящих к их разрушению. Пятый и шестой члены правой части уравнения (1.10) характеризуют изменение импульса г_гфазы за счет дробления (измельчения), а два последних члена — за счет столкновений частиц, не приводящих к их разрушению.

В уравнениях (1.9) и (1.10) 1_х — это изменение импульса несущей фазы за счет измельчения и столкновений частиц всех т дисперсных фаз между собой; 1₂t и 1_3/ — соответственно уменьшение и увеличение импульса одной частицы i-й дисперсной фазы объемом г в результате возможных соударений со всеми частицами объемами от 0 до Л всех дисперсных фаз, которые не приводят к разрушению; гщ) = —Гщ) — объемная сила, отнесенная к единице объема смеси и обусловленная взаимодействием между несущей фазой и одной частицей г_гфазы внутри объема V за счет сил трения, давления, сцепления, эффекта присоединенных масс и т. д.

Объемную силу взаимодействия между несущей фазой и г_гфазой можно представить в виде [531.

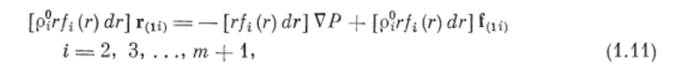
где [plrfi (г) dr] — масса r_rфазы в единице объема;[r/_f (г) dr] — объемное содержание г_гфазы в единице объема смеси (объем всех частиц i-й дисперсной фазы объемом от г до г -}- dr). В правой части выражения (1.11) первое слагаемое связано с воздействием поля давления на частицы (архимедова сила), авторов — со скоростной неравновесностью между несущей и г, — фазой (несовпадением _г и v_{— (г)), которая в общем случае обязана трем эффектам: действию стоксовой силы трения, эффекту присоединенных масс и дополнительному воздействию на г_гфазу, возникающему из-за градиентов в поле средних скоростей несущей фазы. Тогда силу f_(1/) можно представить суммой трех слагаемых f_(li) = f (F,) 4- f (mi) + hrih где f (Po — стоксова сила трения; f_(m/) — сила, связанная с взаимодействием присоединенных масс; l'_(rJ) — сила Магнуса или Жуковского.

Для сил f (_m/) и можно записать¹ соотношения [531.

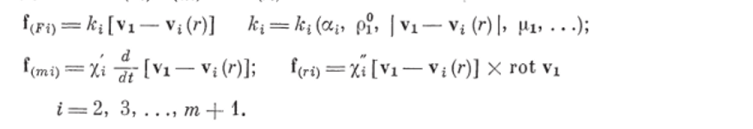
Влияние формы частиц, их неодиночность и другие уточнения в выражениях для сил f (ri) учитываются коэффициентами.

*/. Xi> Xi;

Дифференциальные уравнения. Для вывода дифференциальных уравнений сохранения массы и импульса воспользуемся формулой Остроградского—Гаусса.

Применим формулу (1.12) к интегральным уравнениям сохранения массы (1.7) и (1.8):

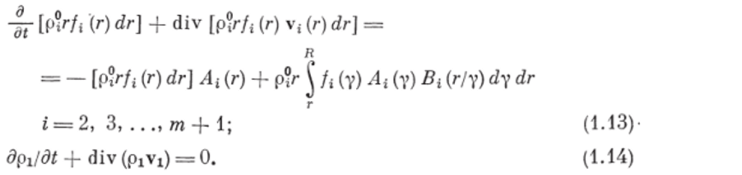
Для рассматриваемой системы, состоящей из многофазной смеси и рабочих органов, с учетом допущения 10 о постоянстве массы рабочих органов запишем закон сохранения массы (изменение массы системы, в которой протекает процесс измельчения—смешения, равно нулю).

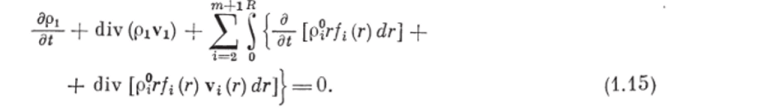
Подставляя в (1.15) правые части уравнений (1.13) и (1.14), получим закон сохранения массы т дисперсных фаз при измельчении.

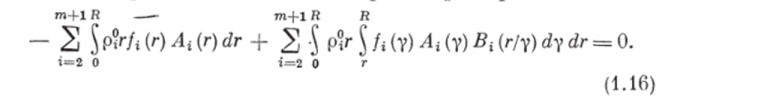
Введем среднемассовую скорость частиц i-й дисперсной фазы.

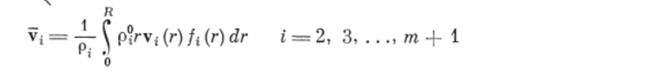
и «диффузионный поток» частиц объемом г i-й дисперсной фазы, определяемый относительно движения частиц со среднемассовой скоростью.

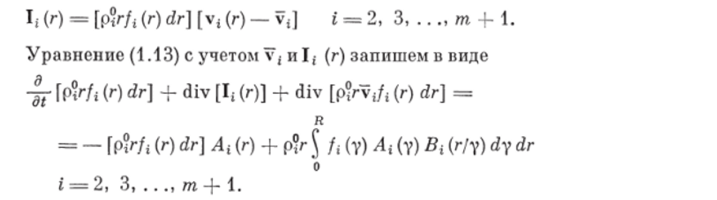
«Диффузионный поток» l_t (г) в первом приближении можно представить.

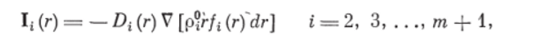
где D_t (г) — коэффициент «макродиффузии» частиц объемом г i-й дисперсной фазы.

Учитывая последнее выражение для I* (г), а также допущение 7, и сокращая левую и правую части уравнения (1.13) и уравнения с учетом Ij (г) и Vj на p? rdr, получаем два варианта записи дифференциального уравнения баланса числа частиц объемом г i-й дисперсной фазы.

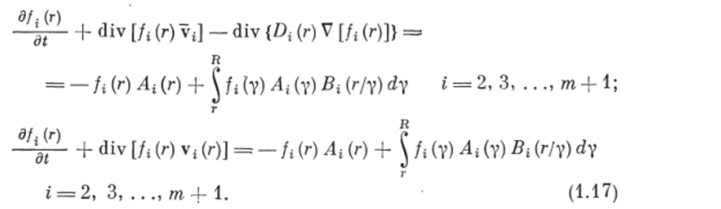
Перейдем к выводу дифференциальных уравнений сохранения импульса. Среди дифференциальных операций тензорного поля особо важное значение в механике сплошных сред имеет операция, аналогичная дивергенции div, а в поле вектора а, но производимая над тензором второго ранга [561. Мы будем обозначать эту операцию тем же символом, что и в случае дивергенции вектора, и применять формулу Остроградского—Гаусса (1.12) для преобразования тензорных величин.

Определим выражения 1₂,-, и 1_3/, характеризующие соответственно уменьшение и увеличение импульса одной частицы объемом [г, г 4- 4- dr] за счет столкновений. Будем рассматривать парные упругие столкновения частиц, не приводящие к их разрушению или агрегации. Тогда частица объемом г г-й дисперсной фазы в результате возможных соударений со всеми частицами объемов [0, Я1 т дисперсных фаз теряет импульс.

где Эij (г, у) — вероятность столкновения частицы из г_;-фазы с частицей из у^-фазы (у_;-фаза представляет собой совокупность частиц объемами от у до у 4- dy й дисперсной фазы); v* (г) — скорость частицы объемом г г-й дисперсной фазы; (г, у) — скорость частицы объемом г г-й дисперсной фазы после столкновения с частицей объемом у ;-й дисперсной фазы.

Преобразуем первое и второе слагаемые правых частей уравнений (1.18) и (1.19). Согласно допущению 9 о}* = —P6^hl 4-о** = = 0. Тогда V^AOi = — VP 4- V^a‘t{. С учетом выражения (1.11) и равенства r_(li) = —-г₍л) получим.

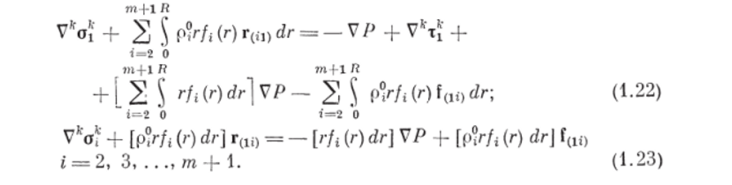
Применяя формулу (1.12) к интегральным уравнениям (1.9) и (1.10), получим.

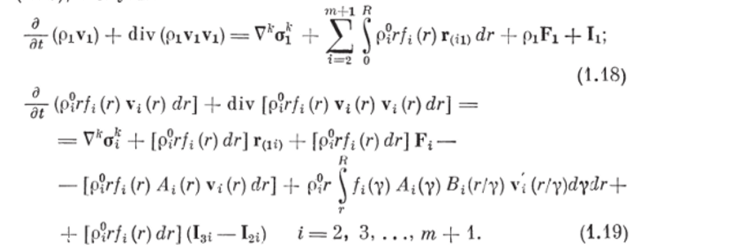
Группируя в правой части выражения (1.22) члены с VP и учитывая, что.

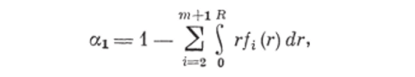
получим.

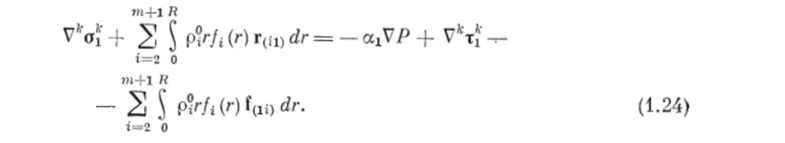
Подставим выражения (1.20), (1.21), (1.23) и (1.24) в уравнения (1.18) и (1.19) и получим.

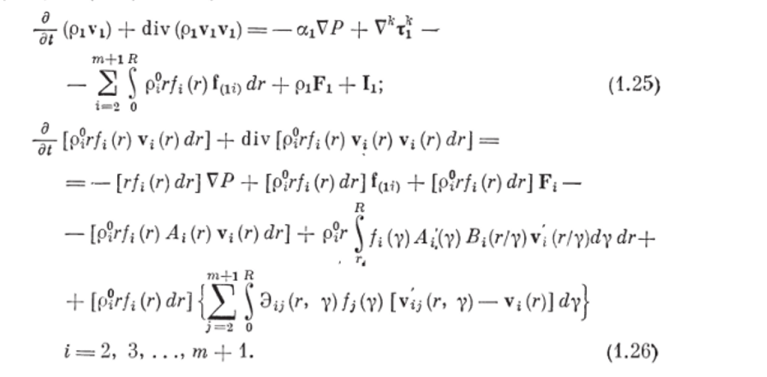
Для рассматриваемой системы, состоящей из многофазной смеси и рабочих органов, с учетом допущения 10 о постоянстве импульса рабочих органов запишем закон сохранения импульса (изменение импульса системы, в которой протекает процесс измельчения—смешения, равно действию поверхностных и массовых сил) в виде.

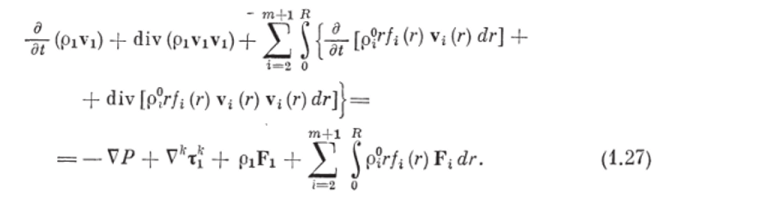
Первые два члена правой части выражения (1.29) определяют изменение импульса несущей фазы за счет измельчения, а последний член — за счет столкновений частиц, не приводящих к их разрушению.

При упругих соударениях частиц, не приводящих к их разрушению или агрегации, избыток импульса распределяется между частицами и не передается несущей фазе, т. е. последний член в выражении (1.29) должен быть равен нулю. Докажем это положение. Скорость частицы объемом г г-й дисперсной фазы после упругого столкновения с частицей объемом у /-й дисперсной фазы равна [57].

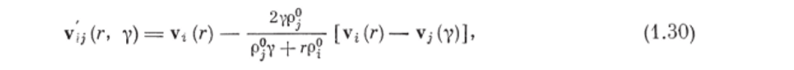
Если в выражение (1.27) подставить правые части уравнений (1.25) и (1.26), то из полученного равенства можно определить в явном виде I_lt характеризующее изменение импульса несущей фазы за счет измельчения и столкновений частиц всех дисперсных фаз в виде.

Сложив соотношения (1.31) и (1.32), получим 2С = 0 или С = 0, что и требовалось доказать. Окончательное выражение для 1₂ будет иметь вид.

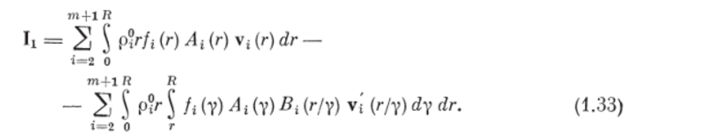
где v_;— (у) — скорость частицы объемом у /-й дисперсной фазы. Обозначим последний член в (1.29) через С, тогда, учитывая (1.30), получим.

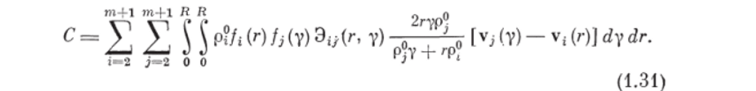
Предполагая, что функция Эц (г, у) симметрична, т. е. Э_и (г, у) = = Эл (у, г), выражение (1.31) представим в виде.

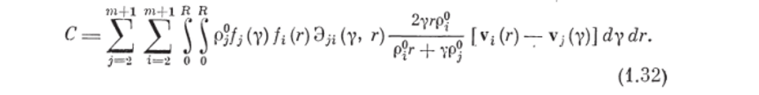
Определим для каждой фазы оператор субстанциональной производной.

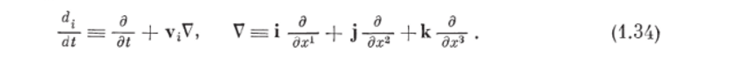
Преобразуем левые части уравнений (1.25) и (1.26) и получим.

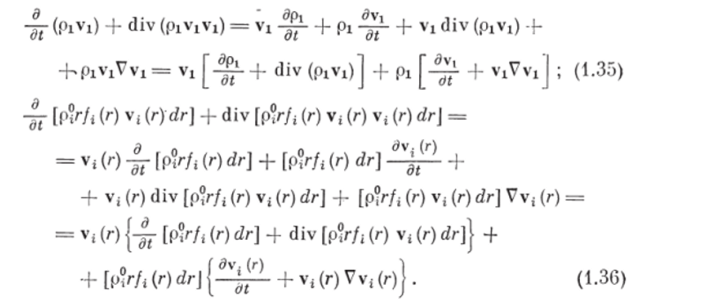
Выражения в первой квадратной скобке в (1.35) и в-первой фигурной скобке в (1.36) представляют собой левые части уравнений сохранения массы соответственно несущей фазы (1.14) и г_гфазы (1.13), а выражения во второй квадратной скобке в (1.35) и во второй фигурной скобке в (1.36) представляют собой согласно (1.34) субстанциональные производные соответственно скорости несущей и г_гфазы. Учитывая это, (1.35) и (1.36) можно преобразовать к виду.

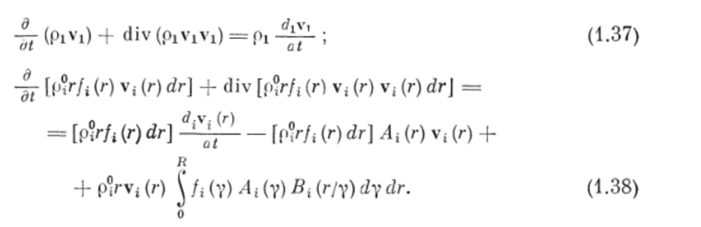
Подставляя выражения (1.33) и (1.37) в уравнение (1.25), а выражения (1.30) и (1.38) в уравнение (1.26), сокращая обе части уравнения (1.26) на rdr и группируя одинаковые слагаемые, получим дифференциальные уравнения движения несущей и г_гфазы в виде.

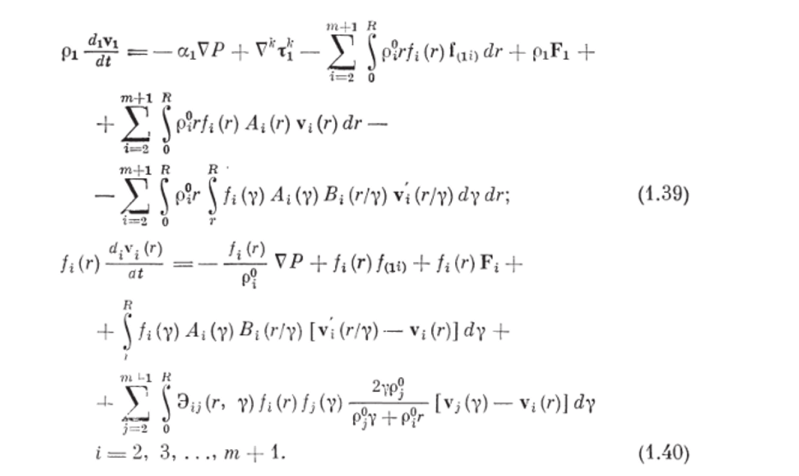
Уравнения изменения внутренних энергий фаз. Полная энергия рассматриваемой системы слагается из внутренних и кинетических энергий несущей фазы, т дисперсных фаз и рабочих органов. Учитывая допущение 12 об аддитивности энергии по массе фаз, можно.

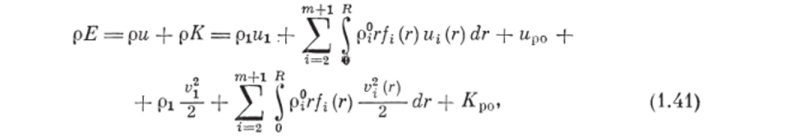
где Е, и, К — соответственно удельные (на единицу массы) полная" внутренняя и кинетическая энергии системы; u_lt (г) — удельные (на единицу массы) внутренние энергии несущей фазы и частицы объемом г i-й дисперсной фазы; и_ро, К_ро — внутренняя и кинетическая энергии рабочих органов, приходящиеся на единицу объема.

В (1.41) учитывается только часть кинетической энергии многофазной смеси, которая связана с массовыми скоростями фаз (кинетической энергией мелкомасштабных течений пренебрегаем).

Для проведения дальнейшего качественного анализа поведения рассматриваемой системы будем использовать уравнения изменения внутренней энергии несущей и /у фазы многофазной смеси 1521 и уравнение измененпя внутренней энергии рабочих органов:

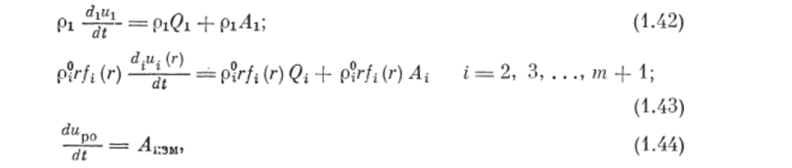
где Q_x и Qi — удельные (на единицу массы) притоки тепла к несущей и /уфазе в единицу времени; А_х и Л* — удельные мощности внутренних сил несущей и г_гфазы; Л"_ям — работа рабочих органов, затрачиваемая на измельчение частиц всех дисперсных фаз, приходящаяся на единицу объема смеси за единицу времени.

Запишем выражение для притока тепла к несущей фазе в виде.

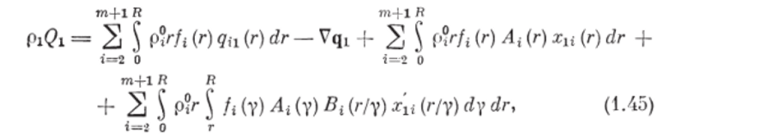
где Qn (г) — удельный поток тепла от частицы объемом г i-й дисперсной фазы к несущей фазе за единицу времени; q, — внешний поток тепла, отнесенный к единице объема смеси; х_и (г) — удельный поток тепла в несущую фазу при разрушении частицы объемом г i-й дисперсной фазы в единицу времени; ду (г/у) — удельный поток тепла в несущую фазу при образовании частицы объемом г i-й дисперсной фазы из частицы объемом у в единицу времени.

где x_L (г) — удельный поток тепла от частицы объемом г i-й дисперсной фазы в результате ее разрушения в единицу времени; х (rly) — удельный поток тепла к частице объемом г t-й дисперсной фазы при ее образовании из частицы объемом у в единицу времени.

Учитывая, что всю работу, но измельчению дисперсных фаз совершают рабочие органы, запишем соотношения для мощности работы внутренних сил несущей и /уфазы в единице объема в виде.

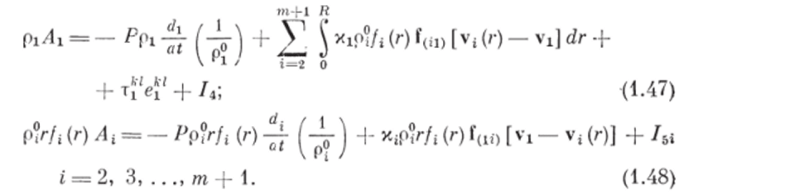
В выражениях (1.47) и (1.48) первые слагаемые определяют мощность работы сил давления при изменении объема несущей и /уфазы, вторые слагаемые определяют часть диссипируемой кинетической энергии всей смеси из-за силового взаимодействия фаз, переходящую непосредственно во внутреннюю энергию соответственно несущей и /уфазы. Коэффициенты и x_f показывают долю этой диссипнруемой энергии, причем х₄ = 1. Третье слагаемое в выражении.

(1.47) определяет мощность работы тензора вязких напряжений в единице объема. Слагаемое /₄ в (1.47) характеризует часть диссшшруемой кинетической энергии всей смеси за счет измельчения и смешения частиц дисперсных фаз, переходящую непосредственно во внутреннюю энергию несущей фазы в единице объема смеси, а слагаемое I si в (1.48) определяет часть диссипируемой кинетической энергии всей смеси за счет измельчения, смешения и столкновений частиц дисперсных фаз, переходящую непосредственно во внутреннюю энергию /уфазы в единице объема смеси.

Подстарляя выражения (1.45) — (1.48) в уравнения изменения внутренних энергий несущей и /уфазы (1.42) и (1.43), получим.

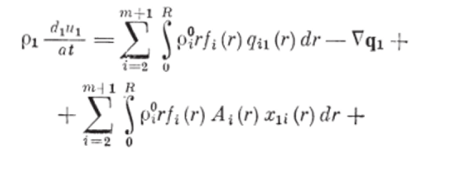
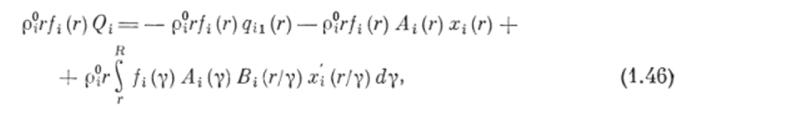
Для получения окончательного вида уравнений изменения внутренних энергий составляющих рассматриваемой системы (1.49) — (1.51) необходимо определить в явном виде условия, которым должны удовлетворять величины х_и (г), х’ц (г/у), /₄, x_t (г), х (г/у), /₅&# Эти условия будем находить из явной записи закона сохранения полной энергии системы (многофазная смесь и рабочие органы). Но для этого сначала определим выражение для работы Л"_ам, совершаемой рабочими органами по измельчению частиц дисперсных фаз.

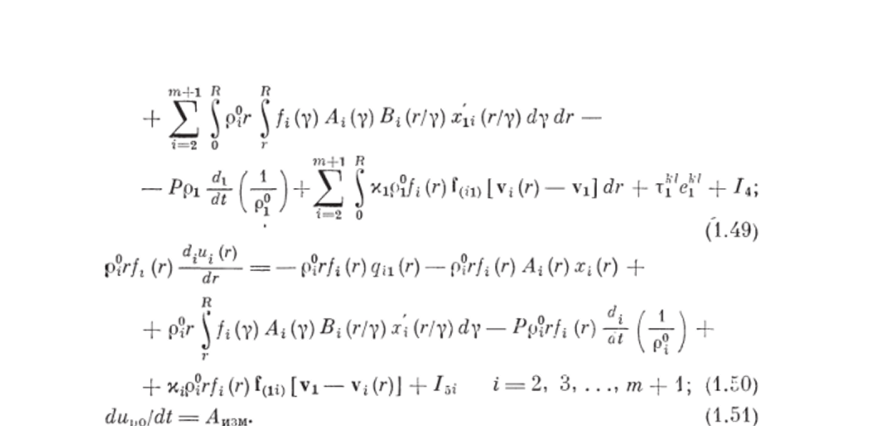
В п. 1.1.1 при рассмотрении смыслового аспекта качественного анализа структуры процесса измельчения — смешения на первом уровне иерархии физико-механических эффектов отмечалось, что измельчение сыпучих материалов всегда сопровождается появлением новых поверхностей. Основной характеристикой поверхности твердой частицы является так называемая поверхностная энергия 1581- одна из физико-механических свойств твердого тела.

Рассмотрим основные понятия о поверхностной энергии твердых тел. Частица кристаллической решетки (атом, ион или молекула) твердого тела, расположенная внутри тела, испытывает силы взаимодействия со стороны всех окружающих ее соседних частиц и находится в состоянии равновесия. Равнодействующая всех сил со стороны окружающих частиц на эту частицу равняется нулю (58]. В иных условиях находится частица твердого тела, расположенная на его поверхности, так как взаимодействующие с ней частицы находятся только с одной стороны — со стороны тела. Это относится к тому случаю, когда твердое тело находится в вакууме. Для того чтобы при таком несимметричном силовом поле равнодействующая всех сил, действующих па поверхностную частицу, равнялась нулю, т. е. чтобы поверхностная частица находилась в равновесии, частицы твердого тела на поверхности должны располагаться иначе, чем во внутренних участках тела. Эти частицы и образуют поверхностный слой [581. Если твердое тело помещено в какую-нибудь среду, то, конечно, поверхностная частица притягивается частицами среды и уменьшает энергию связи поверхностных частиц твердого тела.

Силы взаимодействия между частицами твердого тела быстро убывают с увеличением расстояния между ними. Расстояние между частицами в твердом теле можно считать ~10″ ⁸ см. Толщина поверхностного слоя должна иметь порядок расстояния взаимодействия частиц. Можно считать, что уже на расстоянии в 10^-7 см взаимодействием между частицами можно пренебречь, следовательно, толщина поверхностного слоя может быть равной 1СГ⁸—10~⁷ см.

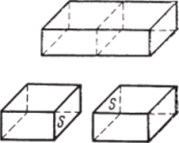
Рис. 1.5. Увеличение поверхностной энергии при разрушении частицы.

Чтобы переместить внутреннюю частицу твердого тела (атом, ион или молекулу) на поверхность, нужно совершить определенную работу, которая переходит в потенциальную энергию поверхностной частицы. Из этого вытекает, что все частицы в поверхностном слое обладают большим запасом потенциальной энергии, чем внутренние частицы, и на поверхности твердого тела сосредоточивается избыток энергии по сравнению с энергией тех объемных частиц, которые образовали поверхностный слои. Этот избыток энергии поверхностного слоя, отнесенный к единице площади, называется удельной поверхностной энергией. Обычно слово «удельная» опускается и говорится просто о поверхностной энергии.

Всякое твердое тело обладает внутренней и поверхностной энергией. Внутренняя энергия измеряется той работой, которую нужно затратить, чтобы разделить твердое тело на частицы (атомы, ионы или молекулы) и удалить их на такие расстояния друг от друга, при которых прекращается взаимодействие между ними. Эта внутренняя энергия пропорциональна объему тела и для двух тел одного и того же вещества, имеющих одинаковые объемы, одинакова.

Кроме того, твердое тело обладает поверхностной энергией, которая пропорциональна поверхности. Следовательно, «полная» внутренняя энергия твердого тела состоит из внутренней и поверхностной энергий, причем поверхностная энергия не является какой-то особой формой энергии. Она определяет только избыток энергии, которым обладают атомы, ионы или молекулы поверхностного слоя по сравнению с атомами, ионами или молекулами внутри тела вследствие их исключительного положения [59]. В силу допущения 12 мы не будем учитывать особенности поверхностного слоя порядка радиуса молекулярного взаимодействия. Это значит, что из «полной» внутренней энергии измельчаемой частицы не будем выделять ее поверхностную энергию. Однако изменение поверхностной энергии измельчаемых частиц будем учитывать в уравнениях изменения внутренней энергии несущей, г_гфазы и рабочих органов.

Для определения Л"_зм проведем ряд рассуждений. Возьмем какую-нибудь частицу i-й дисперсной фазы и обозначим ее «полную» внутреннюю энергию (внутреннюю и поверхностную) через uf (рис. 1.5). Разделим мысленно эту частицу какой-либо плоскостью на две части и обозначим через и* энергию первой части, через и?* —.

Если теперь фактически расколем частицу на две части, то для этого мы должны затратить некоторую энергию, в результате появятся две новые поверхности с площадью S каждая. Теперь уже энергия двух этих частей и** будет на u*_l2)i меньше, чем энергия целой частицы.

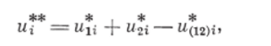
или, учитывая (1.52),.

Под внутренней энергией твердого тела мы условились подразумевать ту работу, которую необходимо затратить, чтобы твердое тело разделить па частицы (атомы, ионы или молекулы) и удалить их друг от друга на такие расстояния, чтобы между ними не было взаимодействия. Часть этой работы н$ 2)1 мы уже затратили на это разделение.

Именно эту работу U ($₂)i ^и будут совершать рабочие органы при разрушении одной частицы i-й дисперсной фазы. Для всех частиц т дисперсных фаз можно записать соотношение типа (1.53).

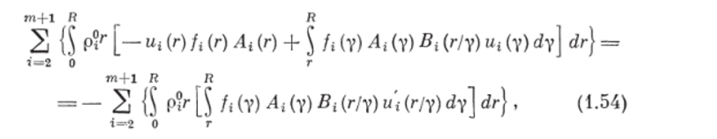
где выражение в правой части определяет работу, совершаемую рабочими органами по измельчению всех частиц т дисперсных фаз в единице объема в единицу времени, а и (г/у) — это работа рабочих органов, затрачиваемая на образование частицы объемом г i-й дисперсной фазы при разрушении частицы объемом у в единице объема смеси, приходящаяся на единицу массы частицы объема г.

Таким образом, работа Л_изм, производимая рабочими органами и затрачиваемая на измельчение частиц дисперсных фаз в единице объема смеси за единицу времени, равна.

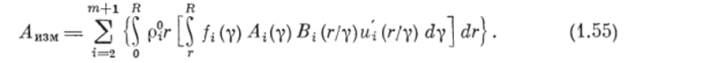
Сформулируем закон сохранения полной энергии системы (несущая фаза — измельчаемые и смешиваемые частицы т дисперсных фаз — рабочие органы): изменение полной энергии системы в единице объема определяется только внешними воздействиями. Запишем где Е1, Ei (г) — удельные полные энергии на единицу объема смеси несущей и г_гфазы; E_t = щ + v!2 Е_к (г) = u_t (г) -|- v< (г)/2; Е_ро — полная энергия рабочих органов, приходящаяся на единицу объема смеси; Е_ро = и_ро 4- К_ро.

Преобразуем выражения в левой части равенства (1.56), учитывая уравнения сохранения массы несущей и г,-фазы (1.13), (1.14), а также формулу (1.34), в виде.

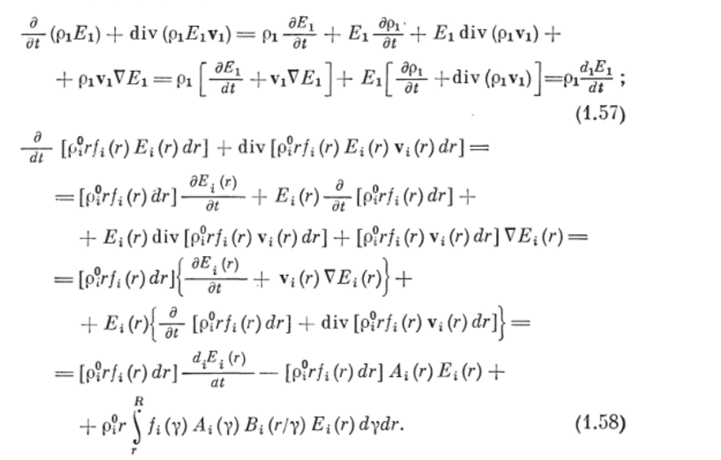
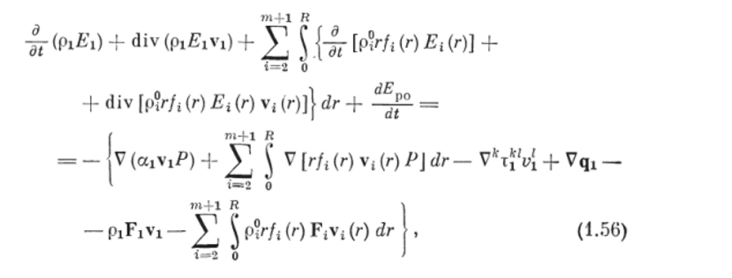
С учетом допущения 10 изменение полной энергии рабочих органов будет равно изменению только их внутренней энергии, т. е.

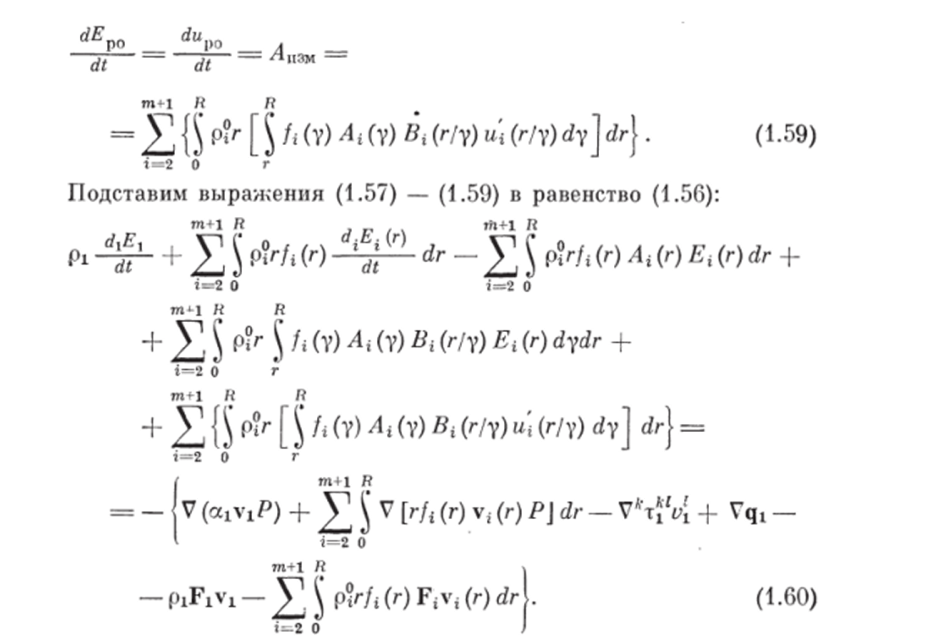
Выражение в левой части называется субстанциональной производной полной энергии системы (несущая фаза — измельчаемые и смешиваемые частицы дисперсных фаз — рабочие органы) и обозначается рDEIDt. Производная рDElDt определяет изменение полной энергии системы в единице объема смеси только за счет внешних воздействий, которые записаны в правой части выражения (1.60).

Чтобы записать в явном виде закон сохранения полной энергии системы, необходимо получить уравнения изменения кинетических энергий несущей и г_гфазы. Для этого умножим дифференциальные уравнения движения несущей и г_гфазы (1.39) и (1.40) на соответствующие значения скоростей фаз v_t и v_f (г):

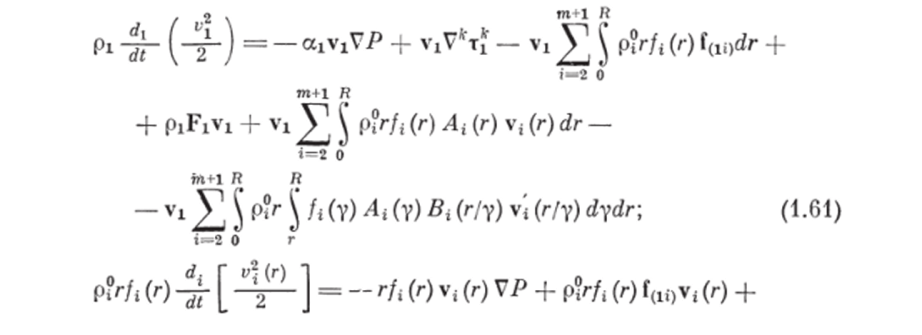
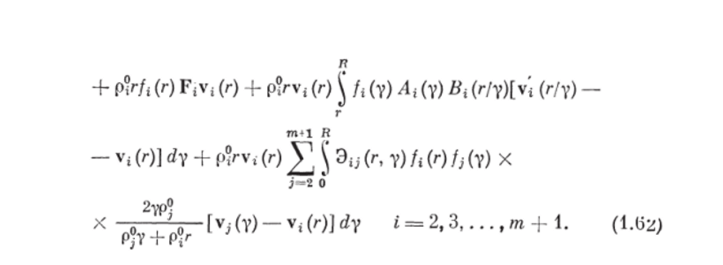
Представим субстанциональные производные полной энергии несущей и гуфазы через субстанциональные производные внутренней и кинетической энергии этих фаз:

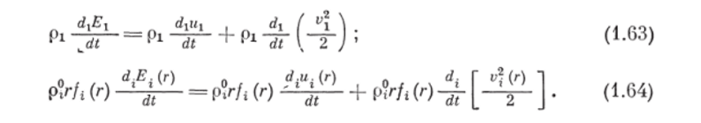
Подставляя в (1.63) уравнения (1.49) и (1.61), в (1.64) — уравнения (1.50) и (1.62), а их в свою очередь в (1.60), определим в явном виде выражение для субстанциональной производной полной энергии системы:!

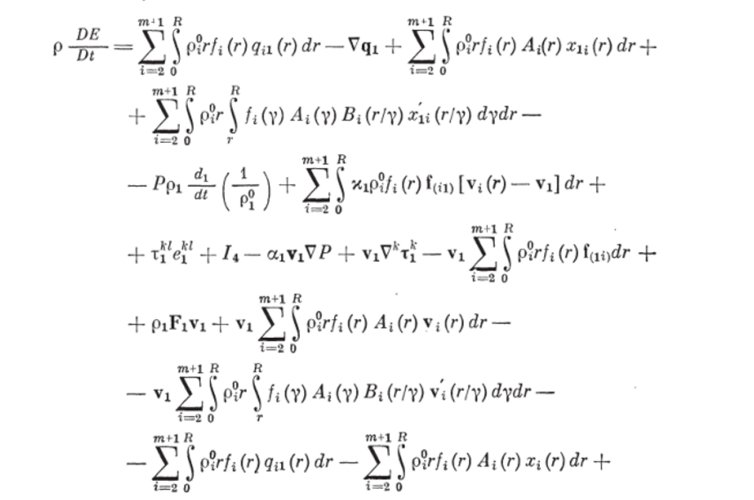
Из уравнений сохранения массы несущей и г_гфазы (1.14) п (1.13) выразим производные d^/dt и diptydt, преобразовав предварительно.

Выражение в фигурных скобках в правой части (1.71) согласно (1.16) равно нулю. С учетом этого (1.71) после группирования слагаемых представим в виде.

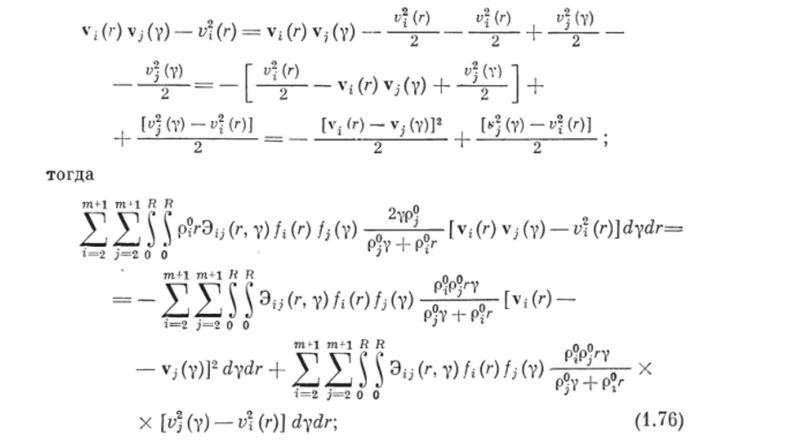
последнее слагаемое в (1.76) равно нулю (доказательство аналогично (1.31), (1.32)).

Учитывая (1.75) и (1.76), запишем в окончательном виде выражение для субстанциональной производной полной энергии системы в виде.

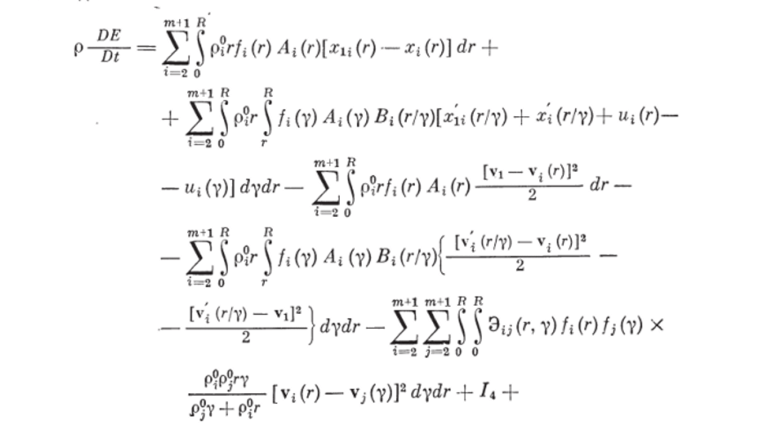
Таким образом, мы получили явную запись выражения для субстанциональной производной полной энергии системы (несущая фаза — измельчаемые и смешиваемые частицы т дисперсных фаз — рабочие органы), которая согласно закону сохранения полной энергии системы (1.60) определяет изменение полной энергии системы в единице объема смеси только за счет внешних воздействий.

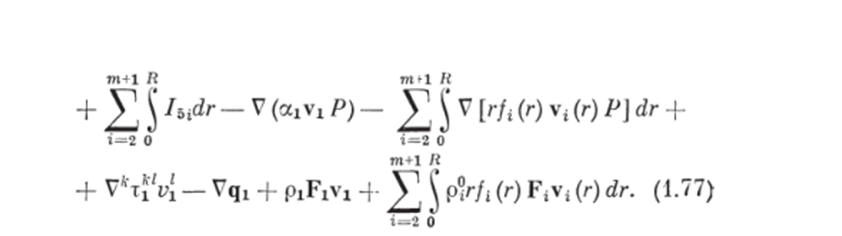
Это значит, что первые семь слагаемых в (1.77), характеризующие источники энергии за счет измельчения, смешения и соударений частиц дисперсных фаз, должны равняться нулю, т. е. можно записать условия для определения величин х_и (г), хц (r/у), /₄, x_t (г), х. (Ну) и I_5i:

Подставляя (1.55) и (1.81) — (1.85) в уравнения (1.49) — (1.51)_t получим окончательный вид уравнений изменения внутренних энергий составляющих рассматриваемой системы:

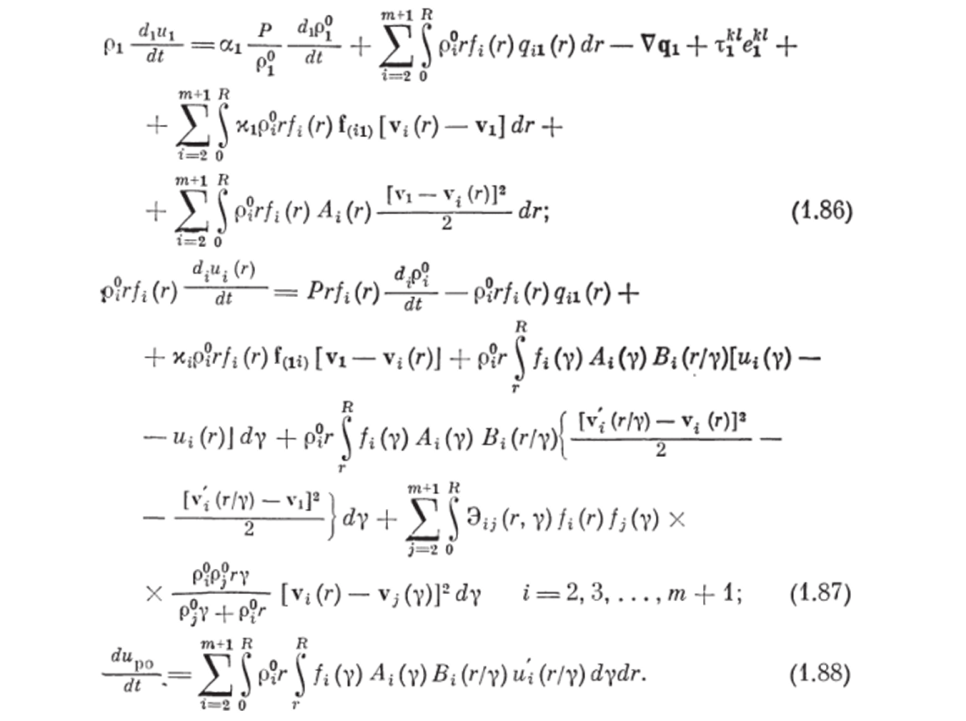
Таким образом, обобщенное математическое описание системы (несущая фаза — измельчаемые и смешиваемые частицы — рабочие органы), которое описывает движение многофазной полидисперсной смеси с учетом измельчения, смешения и столкновений частиц, имеет вид Тогда из (1.78) следует а из (1.79).

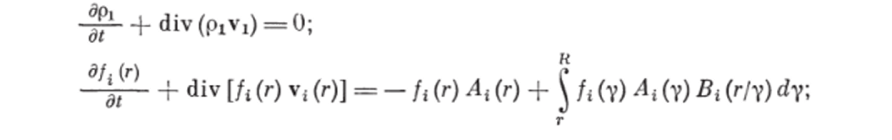
= 1, х* = 0. Зависимости для A_t (г), /?, (г!у) и Эц (г, у) определяются из структуры движущих сил строго аналитически и затем на третьем этапе системного анализа процесса измельчения—смешения уточняются экспериментально. Выражение для скорости частицы объемом г, образованной при разрушении частицы объемом у, и (г!у) зависит от конструкции рабочих органов, а значит, и от способа измельчения; для конкретного измельчающего аппарата будет и свое выражение для и] (rly). Выражения для v (rJy) будут получены в гл. 2 для измельчающих аппаратов ударного типа.