Оценка надежности схем электрических соединений

Выбор схем электрических соединений подстанций и сетей часто происходит на основании рекомендаций, приведенных в различных нормативных документах, но без количественной оценки их надежности. При выборе схемных решений по сетевым районам и подстанциям не учитывается появление новых видов высоконадежного электрооборудования, а соответственно возможное рациональное упрощение схем. Такое положение приводит к тому, что в ряде случаев принимаются неоптимальные, с точки зрения экономичности и надежности, решения. Поэтому актуальной остается задача разработки и совершенствования методик оценки надежности схем электрических соединений подстанций и количественных показателей надежности при сравнении различных вариантов схем. Актуальность создания и совершенствования методик расчета надежности вызвана возникающей неопределенностью. Нередко на основании действующих нормативных документов невозможно принять решение об окончательном выборе между несколькими рассматриваемыми вариантами.

Задача оценки показателей надежности сводится к расчету конкретных значений вероятностей безотказной работы схемы по информации об усредненных значениях параметра потока отказов для единицы оборудования и среднем времени его восстановления в течение определенного периода. Далее, по значению ВБР (вероятности отказа) того или иного элемента сети (трансформатора, генератора, линии, присоединения) определяются показатели для схемы в целом.

Основными задачами, решаемыми при проектировании схем электрических соединений, в которых необходим учет надежности в виде ряда показателей или нормативов, являются:

• — разработка требований и принципов управления схемой в нормальных и аварийных режимах;
• — получение достоверной информации о единичных показателях надежности нового оборудования;
• — определение требований и оценка допустимости технического обслуживания и ремонта электрооборудования проектируемых энергообъектов по плановым и аварийным заявкам;
• — выбор схем коммутации проектируемого энергообъекта;
• — расчет комплексных показателей надежности основной проектируемой структуры энергообъекта.

На сегодняшний день не существует универсального метода расчета надежности схем электрических соединений, хотя имеется большое число частных методов, основными из которых являются: аналитический; таблично-логический; метод, использующий теорию марковских процессов; метод дерева отказов и др. Отличительные особенности их определяются уровнем допущений, полнотой учитываемых факторов, структурой и содержанием требуемой исходной информации. Известно, что применение их для оценки надежности одной и той же схемы приводит к результатам, порой отличающимся на порядок. Основная причина этого — практическое отсутствие научно обоснованных рекомендаций для конкретного применения каждого из них. Следует отмстить, что даже специально проведенные фундаментальные исследования не привели к окончательному решению поставленной проблемы, поскольку не разрешен ряд противоречий и не устранены недостатки, затрудняющие их практическое использование, в числе их:

• — существующие методы анализа надежности предполагают индивидуальный детальный анализ каждой схемы;
• — разные методы предлагают разные критерии оценки надежности;
• — для расчета надежности гребуется разработка специальных алгоритмов и выбор индивидуальных ограничений;
• — неудовлетворительная наглядность рекомендуемых схем замещения приводит к неучету ряда влияющих на надежность факторов;
• — затруднена комплексная оценка показателей надежности схемы энергообъекга (подстанции, сети, района).

В этой связи предлагается матричный метод оценки надежности схем распределительных устройств подстанций, который позволяет устранить большинство из выявленных недостатков. Для этого вводится следующая классификация элементов схем:

• — активные — элементы, которые при повреждении смежных элементов могут отключить участок поврежденной сети, т. е. выключатели;
• — пассивные — другие элементы схемы, которые при повреждении смежных элементов не могут локализовать повреждение;
• — расчетные — элементы, для которых непосредственно определяются количественные показатели надежности;
• — смежные — элементы, связанные с расчетными электрической связью.

Надежность каждого элемента сети предлагается определять двумя составляющими: собственной надежностью и надежностью элементов, связанных с ним.

Влияние смежных элементов на надежность расчетного определяется схемной удаленностью их от расчетного. Надежность расчетного элемента определяется по формуле.

где оу, — параметр потока отказов расчетного элемента;

«1, яг* •••* «я «условная вероятность отказа активного элемента при отключении поврежденного участка сети, 1 > а» >0;

ас*о" а>с*ь —" Юеия «параметры потока отказов смежных элементов.

Физический смысл выражения (10.24) состоит в том, что отказ смежного элемента, не отделенного от расчетного выключателем, приводит к отказу расчетного элемента. При отказе смежного элемента, отделенного от расчетного одним выключателем, отказ расчетного элемента произойдет при условии отказа выключателя, что в формуле (10.24) учитывается условной вероятностью <2/. Аналогично, если элемент находится за двумя выключателями от расчетного, величина? o_CW2 умножается на условную вероятность отказа этих двух выключателей (а, • а₂), и т. д.

Очевидно, что возможен учет влияния смежных элементов, как угодно далеко находящихся от расчетного (п = «>). Однако, учитывая реальные значения условных вероятностей отказов для различных типов выключателей (со_с/, = 0,02), очевидно, что учет слагаемого а • а₂? ®см2 (смежный элемент за вторым выключателем) уже практически не даст существенного уточнения результата (а² = 0,0004). Поэтому в расчетной схеме замещения целесообразно учитывать только те элементы, которые находятся не далее чем за одним активным от расчетного.

На основании однолинейной схемы подстанции и в соответствии с принятой классификацией элементов составляется схема замещения. Опираясь на схему замещения, составляем три матрицы.

1. Матрица связей S. Прямоугольная матрица порядка М х /V, где М — количество расчетных элементов, N ~ общее количество элементов. Элемент матрицы Sy может иметь три значения.

2. Матрица времени восстановления Т. Матрица того же порядка, что и матрица S. В нее заносятся значения времени восстановления элементов ty.

где.

tg — среднее время восстановления смежного элемента сети;

t — среднее время производства оперативных переключений, необходимых для локализации повреждения.

3. Матрица параметров потока отказов ?2. Квадратная матрица порядка N * N, в которую по главной диагонали заносятся значения параметра потока отказов всех элементов, включенных в схему замещения. Остальные ее элементы — нули.

Наличие этих матриц позволяет путем несложных преобразований получить показатели надежности для расчетных элементов. Умножая матрицу Т на матрицу ?2, получим промежуточную прямоугольную матрицу порядка Af х N, элементы которой равны коэффициентам вынужденного простоя расчетных элементов при отказах элементов сети.

Умножая матрицу S на транспонированную матрицу К¹, получим результирующую матрицу коэффициентов вынужденного простоя С.

Матрица С — квадратная матрица порядка А/ х А/, в которой элементы, расположенные на главной диагонали — вероятности отказа (коэффициенты вынужденного простоя) расчетных элементов в течение года; остальные элементы — вероятности отказа, определяемые влиянием элементов, смежных с расчетными, на надежность расчетных элементов. Операция умножения на коэффициент 1/8760 соответствует приведению коэффициентов вынужденного простоя расчетных элементов к промежутку времени, равному одному году.

Отметим, что представление результатов расчета в вероятностной форме (вероятность отказа) часто не дает полной информации о фактической надежности элемента. При малых вероятностях отказа время восстановления может быть значительным, и тогда проектируемая схема не будет удовлетворять требованиям по бесперебойности и другим показателям надежности электроснабжения. Поэтому в задачах реального проектирования и эксплуатации предлагается использовать комплексный показатель надежности — коэффициент вынужденного простоя, который в количественной форме наиболее наглядно отражает надежность схемы.

Пример. В связи со значительным моральным и физическим износом оборудования, а также предполагаемым в перспективе 5—10 лет вводом в эксплуатацию новых энергообъектов, необходима реконструкция главной схемы действующей подстанции 220 кВ — ПС-1. В настоящее время от нее отходят 5 ВЛ напряжением 220 кВ (рис. 10.12, 10.13).

Принимаем к рассмотрению два варианта схемы: 1. ОРУ 220 кВ по схеме «две рабочие системы шин» (2РСШ) (см. рис. 10.12), 2. ОРУ 220 кВ по схеме «одна рабочая, секционированная выключателем, система шин» (1РСШ) (см. рис. 10.13).

Данная подстанция — узловая, обеспечивает выдачу мощности ТЭЦ-2 и ГЭС-1. На основании расчетов в аварийных режимах не допускается разрыв транзитов по линиям 220 кВ ГЭС-1 — ПС-1 и ПС-1 — ТЭЦ-2. Иначе говоря, отключение этих линий допустимо только на время оперативных переключений. При этих условиях необходимо применить схему 2РСШ. Эта схема, на первый взгляд, действительно удовлетворяет требованиям надежности, т. е. при отключении одной из систем шин все присоединения в кратчайшее время могут быть переведены на другую систему шин.

Однако технические требования к подстанциям 330−750 кВ нового поколения рекомендуют: «Электрические схемы ПС всех напряжений должны быть обоснованно упрошены с учетом применения высоконадежного оборудования. Для РУ 220 кВ и ниже в основном следует применять одинарные секционированные системы шин*. Поскольку однозначный выбор схемы данной подстанции на основании указанных действующих документов сделать нельзя, возникает вопрос, насколько выше будет вероятность разрыва расчетного транзита при погашении секции шин в схеме 1РСШ по сравнению со схемой 2РСШ.

Показатели надежности трансформаторов, линий и сборных шин приняты, но литературным данным (табл. 10.8). Параметр потока отказов для сборных шин учитывает отказы сборных шин (наброс посторонних предметов, разрушение опорной или подвесной изоляции) и отказы при операциях с разъединителями (поломка колонок изоляторов). Показатели надежности элегазовых выключателей усреднены на основании каталожных данных различных производителей.

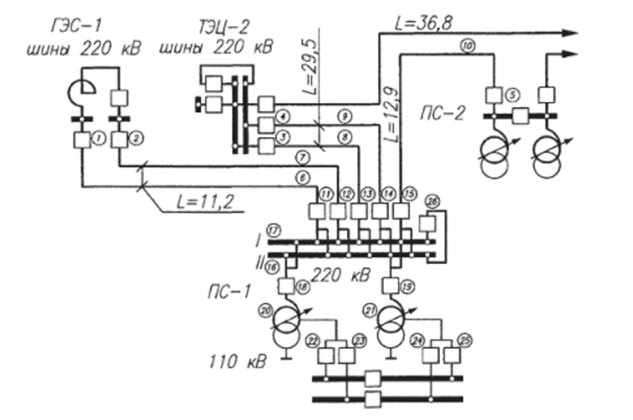
Рис. 10.12. Вариант 1 присоединения ПС-1 к энергосистеме по схеме 2РСШ

Таблица 10.8.

Рис. 10.13. Вариант 2 схемы присоединения ПС-1 к энергосистеме по схеме 1РСШ

Модель отказа выключателя выбрана так, что параметр потока отказов учитывает все аварийные отключения, связанные с его эксплуатацией, а все его повреждения приводят к отключению смежных выключателей — отказ в обе стороны. Схема замещения исходной системы представлена на рис. 10.14.

Рис. 10.14. Схема замещения д. хя расчета надежности в HopMatbHOM режиме д. хя вариантов 1 и 2.

Расчетная схема замещения для нормального режима одинакова для обоих вариантов, так как в схеме с 2РСШ принята фиксация присоединений аналогично схеме 1РСШ. Дальнейшие вычисления приведены для схемы 1РСШ (см. рис. 10.13).

В качестве расчетных элементов принимаем секции (системы) шин (элементы 16, 17). Матрицы связей S, времени восстановления Т и потока отказов Q имеют вид, представленный в табл. 10.9, 10.10, 10.11 соответственно.

Умножив матрицу Т на матрицу О, получим матрицу К (табл. 10.12).

Таблица 10.9.

Продолжение таблицы 10.9.

Таблица 10.10.

Продолжение таблицы 10.10.

Таблица 10.11.

Таблица 10.12.

Продолжение таблицы 10.12.

Продолжение таблицы 10.12.

После умножения матрицы S на транспонированную матрицу № получаем матрицу С, элементы которой:

• • ^си" ^с22 — вероятности отказа (коэффициенты вынужденного простоя) расчетных элементов в течение года;
• • ^с12″ ^С21 «вероятности отказа, определяемые влиянием элементов схемы, смежных с расчетными, на надежность расчетных элементов.

Значение среднего времени / производства оперативных переключений в сети 220 кВ, необходимых для локализации повреждения, принято t = 1 час. Условная вероятность отказа выключателей принята а = 0,01.

Дальнейшие вычисления параметров ремонтного режима проводим, изменяя исходную схему замещения (см. рис. 10.14).

Для схемы 2РСШ (см. рис. 10.12) расчет проводим аналогично, изменяя входные значения параметров надежности для элементов 16 и 17. Разные значения параметра потока отказов для элементов 16 и 17 обусловлены разным количеством присоединений в первом и втором варианте схемы.

где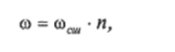

(о_еш — параметр потока отказов для сборных шин (на одно присоединение), 1/год; п — количество присоединений.

Рис. 10.15. Схема замещения для расчета ремонтного режима 1-й секции шин (элемент 17), вариант 1

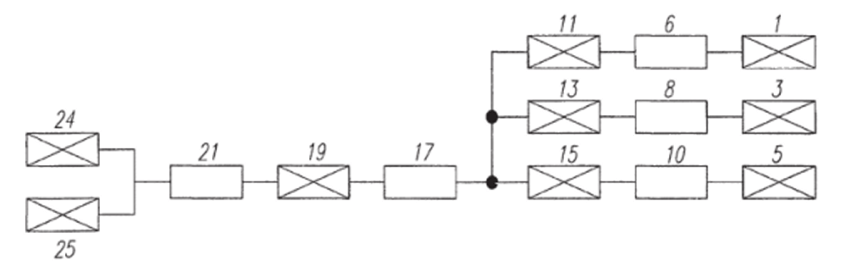
Рис. 10.16. Схема замещения для расчета ремонтного режима 2-й секции шин (элемент 16), вариант 1.

Для варианта 1:

Для варианта 2:

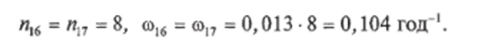
Результаты вычислений сведены в табл. 10.13, где коэффициенты вынужденного простоя (в числителе) представлены в относительных единицах, а в знаменателе — в %. Для удобства сравнения принимаем за 100% минимальные значения:

. коэффициент вынужденного простоя К_вп для 1РСШ (см. рис. 10.13) в нормальном режиме для первой секции — 3,933 • 10'⁵ = 100%;

• коэффициент вынужденного простоя К_впс для 1 PCШ (см. рис. 10.13), определяемый влиянием элементов смежных с расчетными на надежность расчетных элементов для первой секции — 1,325 • 10‘⁵ = 100%.

Таблица 10.13.

?Показатель надежности приведен для оставшейся в работе секции (системы) шин.

Проведём анализ результатов расчета.

Нормальный режим. Коэффициент вынужденного простоя первой секции (системы) шин К_дп (элемент 17), за счет большего количества присоединений, выше, чем в схеме с двумя рабочими системами шин (2РСШ), так и в схеме с одной секционированной системой шин (1РСШ).

Послеаварийный режим (отключение одной секции (системы) шин). Коэффициент вынужденного простоя выше у схемы 2 РСШ за счет большего количества присоединений к секциям шин 8 против 4 и 5 соответственно на 1 и 2 секции у схемы 1 РСШ. Таким образом, вероятность отказа в схеме 2РСШ выше в нормальном режиме по сравнению со схемой 1РСШ.

В ремонтном режиме разница в показателях надежности возросла за счет увеличения числа присоединений в схеме 2РСШ и уменьшения их в схеме 1РСШ.

Таким образом, схема 2РСШ оказывается менее надежной и в нормальном, и в ремонтном режиме по сравнению с 1РСШ. Это объясняется большим количеством присоединений к системе шин в схеме 2РСШ. Существенное влияние на надежность оказывает количество оперативных переключений, которое, очевидно, пропорционально количеству ошибок оперативного персонала. Преимущества предлагаемого метода заключаются в формализованном подходе к составлению схемы замещения и наложению ограничений по количеству рассматриваемых элементов; простоте создания программных продуктов; возможности рассмотрения различных режимов путем простого изменения схемы замещения; возможности расчета надежности схем с большим количеством элементов.