Узкополосные случайные процессы

В теории связи чрезвычайно важен особый класс случайных процессов, односторонний спектр мощности /''(со) (3.31) которых имеет резко выраженный максимум вблизи некоторой центральной частоты со₀, отличной от нуля. Как правило, функция /'(со) симметрична относительно частоты со₀, которая выбрана таким образом, что не содержит слагаемого, линейно зависящего от времени t. Такие сигналы относят к узкополосным случайным процессам. Их рассмотрение в учебнике ограничено стационарными и эргодическими случайными гауссовыми процессами, наиболее часто встречающимися на практике. К тому же именно для гауссовых процессов удается получить ряд важных результатов, не выходя за рамки их корреляционной теории.

Узкополосным называют случайный процесс X (t), односторонний спектр мощности /'(со) которого сосредоточен в полосе частот Дсо (ее часто называют эффективной шириной спектра), значение которой значительно меньше средней частоты со₀, т. е. Дсо <�сС со₀ (рис. 3.19). При этом реализации узкополосного случайного процесса представляют собой квазигармонические колебания, случайно модулированные по амплитуде п фазовому углу. Узкополосными случайными процессами являются модулированные сигналы, принятые и обрабатываемые в приемниках систем передачи информации.

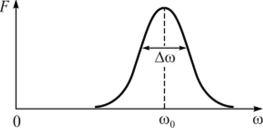
Рис. 3.19. Спектр мощности узкополосного случайного процесса.

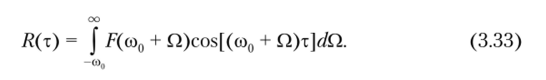
Функция корреляции узкополосного случайного процесса. Рассмотрим узкополосный случайный процесс X (t) с односторонним действительным спектром мощности F (tо). Узкополосный характер спектра F (co) говорит о том, что корреляционная функция /?,(т) должна также иметь вид узкополосного сигнала. Для удобства мысленно сместим спектр случайного процесса F (со) из окрестности частоты со₀ в окрестность нулевой частоты, выполнив замену переменной со = со₀ + Q. Тогда формула (3.29) при частоте со" = со — П примет вид Поскольку спектр мощности F (со) узкополосного процесса X (t) ничтожно мал на частотах, близких к нулю, то в выражении (3.33) можно без заметной погрешности заменить нижний предел интегрированиясо₀ на Тогда функцию корреляции можно записать как где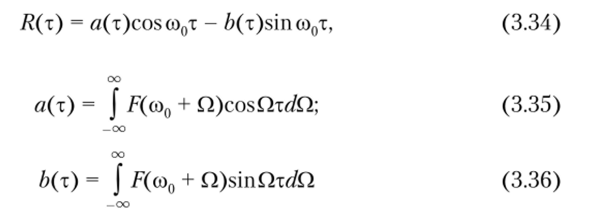

— медленно меняющиеся функции аргумента <�р, причем они представляют собой амплитуды соответственно косинусной и синусной составляющих реализации x (t).

Если узкополосный случайный процесс обладает спектром мощности F (со), симметричным относительно центральной частоты со₍₎, то функция корреляции имеет очень простой аналитический вид. Очевидно, что при этом в формуле (3.34) «синусная» составляющая /?(т) = 0 и функция корреляции R ( т) = tf (x)cosco₀T.

В последнем соотношении параметр а (т) играет роль огибающей функции корреляции, которая изменяется медленно во времени по сравнению с «быстрым» сомножителем cosco₀t. На практике часто вводят нормированную огибающую р (т) функции корреляции, определив ее через дисперсию (квадрат СКО) узкополосного случайного процесса а² с помощью равенства а (т) = ст²р (т) Тогда функция корреляции типичного узкополосного случайного процесса (рис. 3.20) запишется в следующем виде:

aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">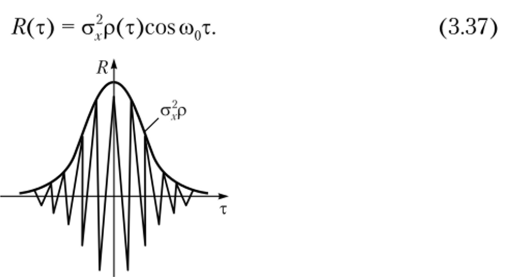

Рис. 3.20. Функция корреляции узкополосного процесса Огибающая и начальная фаза узкополосного случайного процесса. Узкополосный спектр и осциллирующий вид корреляционной функции (3.37) означают, что любая реализация узкополосного случайного процесса представляют собой квази гармонические колебания с периодом Т₀ = 2п/(й₀ (рис. 3.21):

у которых и огибающая ?/(?), и начальная фаза ф (?) являются случайными функциями, медленно (по сравнению с со₀ или cos со/) изменяющимися во времени.

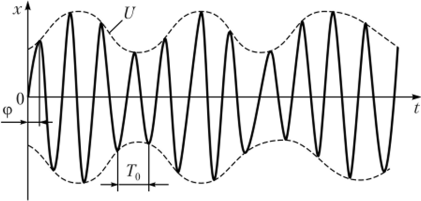
Рис. 3.21. Реализация узкополосного случайного процесса

Представим реализацию колебаний (3.38) как сумму синфазной и квадратурной амплитуд, точнее, квадратурных колебаний или реализаций (2.125):

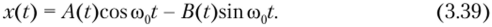
Очевидно, что колебания A (t) и В (!) являются медленно меняющимися функциями, и тем они низкочастотнее, чем меньше эффективная ширина спектра Дсо процесса по сравнению с центральной частотой ю₀.

Введем в рассмотрение узкополосный случайный процесс 7(f), сопряженный с исходным процессом X (t) (кстати, в этом смысле нет различия между случайным и детерминированным процессами). Его одиночной реализацией является реализация (2.136), сопряженная по Гильберту физическому колебанию x (t):

Низкочастотность синфазной A{t) и квадратурной B (t) амплитуд позволяет сравнительно просто записать формулу для реализации сопряженного случайного процесса Y (t), вынеся медленно меняющиеся множители по сравнению с частотой со₀ за знак преобразования Гильберта:

y (t) = B (t)cos (o₀t + Л (?)хтсо₀7. (3.41).

Из формулы (3.41) по аналогии с соотношениями (2.138) и (2.139) получаем формулы для мгновенных значений огибающей физической реализации x{i)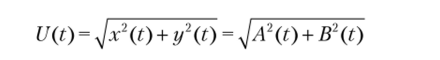

и начальной фазы исходного случайного процесса Х (!)

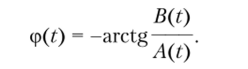
Статистические свойства сопряженного узкополосного случайного процесса. Чтобы изучить основные свойства огибающей и начальной фазы узкополосного случайного процесса, следует определить, есть ли связь между статистическими характеристиками анализируемого X (t) и сопряженного ему Y{t) процессов. Для этого сначала определим математическое ожидание сопряженного случайного процесса, применив усреднение по времени к формуле (3.40):

Как и следовало ожидать, результат усреднения равен нулю, поскольку исходный процесс X (t) является центрированным. Итак, если x (t) = 0, то и y (t) = 0. Далее, вследствие того что процесс Х (1) имеет нормальное распределение, а преобразование Гильберта есть линейное интегральное преобразование, то нормальным будет и сопряженный процесс Y (t). Таким образом, реализации x (t) и y{t) в совпадающие моменты времени некоррелированны. Поскольку они, кроме того, имеют нормальное распределение, то из некоррелированности и следует их статистическая независимость.

Из свойств преобразования Гильберта следует, что спектры конкретных реализаций процессов х (t) и y (t) связаны определенным образом. Как известно, если 5,.((о) — спектральная плотность исходной конкретной реализации д (г), то спектральная плотность сопряженной реализации y (t) равна.

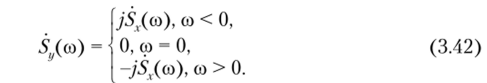
Иногда для удобства формулу (3.42) записывают в более компактном виде:

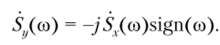
Символом sign (сигнум-функция) обозначается функция.

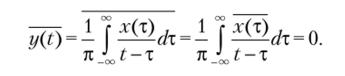
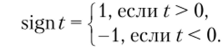
Модули спектральных плотностей 5_v(cо) и 5 (со) совпадают, поэтому спектры мощности процессов X (t) и Y (l) одинаковы: F_x(со) = F {ю). Поскольку функции корреляции связаны со спектрами мощности обратным преобразованием Фурье, то они тоже должны быть одинаковыми, и согласно формуле (3.29) для одностороннего спектра (вместо W (co)/n используем F (cо)).

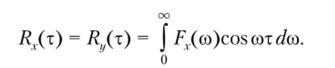
Очевидно, что сопряженный процесс Y (t) является также стационарным.

Определим функцию взаимной корреляции /? (т) реализаций сопряженных узкополосных процессов X (t) и Y (t). Для этого заменим функцию y (t) сопряженной функцией x (t) по выражению (3.40), введем новую переменную временного сдвига реализаций р и затем, проведя несложные преобразования, получим формулу.

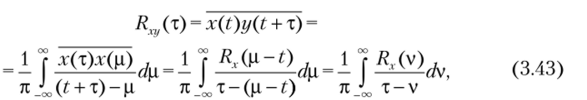
которая соответствует преобразованию Гильберта от функции корреляции исходного процесса X (t). В формуле (3.43) переменная v = ц — t.

Аналогично найдем функцию взаимной корреляции процесса R,_/y(^x)^{: R^zy—R^x).}

Таким образом, используя формулы (2.137) и (3.29), получим.

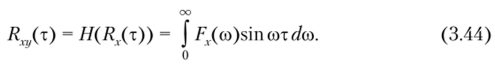
Нетрудно установить, что функция R_xy(^x) нечетна и обращается в нуль при отсутствии сдвига (т = 0). Поэтому процессы X (t) и Y (t) в совпадающие моменты времени статистически независимы (не коррелированны). Формулу (3.44) представляют в более удобной форме, выполнив замену переменной со = со_ц + Q:

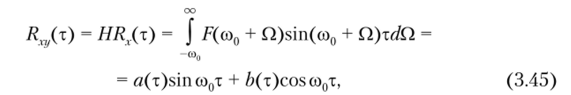
в котором функции а (т) и Ь (х) определяются в соответствии с выражениями (3.35) и (3.36).

Характеристики огибающей U (t) и начальной фазы <�р (?) узкополосного процесса. Для определения вероятностных характеристик перейдем от реализаций x (t), y{t) к низкочастотным синфазной A{t) и квадратурной B (t.) функциям, которые найдем из формул (3.39) и (3.41). После несложных преобразований получим.

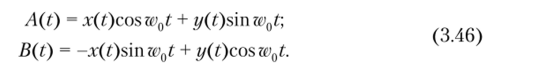
Вычислим функцию корреляции реализации A (t), используя для этого первую формулу из соотношений (3.46). Выполнив элементарные преобразования по усреднению произведения, находим.

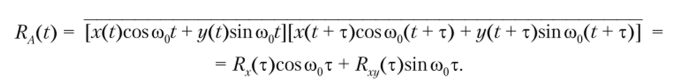
Подставив в это соотношение выражения функций R_x(т) и R (т) из формул (3.34) и (3.45), приходим к очень простому результату /? ,(т) = я (т).

Аналогично можно показать, что функции корреляции реализации B (t) и взаимокорреляционпая функция реализаций A (t) и B (t) соответственно равны.

Положив в формулах (3.47) и (3.48) т = 0, имеем.

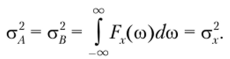
Итак, дисперсии синфазной A (t) и квадратурной B (t) функций для низкочастотных колебаний оказываются равными дисперсии исходного узкополосного процесса X (t).

Двумерная плотность вероятности огибающей и начальной фазы узкополосного случайного процесса. Переход от реализации узкополосного случайного процесса x (t) к ее синфазной A (t) и квадратурной B (t) составляющим существенно упрощает анализ, если требуется вычислить двумерную (совместную) плотность вероятностиp (U> ф) огибающей U (t) и начальной фазы ф (?) узкополосного случайного процесса. Эта характеристика, в свою очередь, дает возможность найти одномерную плотность вероятности огибающей

и одномерную плотность вероятности начальной фазы.

Мгновенное значение комплексного случайного процесса X{t) можно отразить графически с помощью двух составляющих низкочастотных колебаний: синфазной A (t) и квадратурной B (t) (рис. 3.22). Это позволяет сделать предположение о симметричности спектра мощности случайного процесса F (со) и обращении в нуль амплитуды Ь (т) синусной составляющей реализации x (t). Мгновенные значения амплитуд реализаций A (t) и B (t) образуют на комплексной плоскости двумерный гауссов вектор огибающей U (t) (рис. 3.22, а), обе составляющие которого независимы и имеют одинаковые дисперсии а². Поэтому двумерная плотность вероятности квадратурных составляющих реализации случайного процесса х (t) будет.

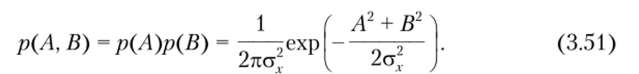
Для определения статистических свойств огибающей и фазы по формуле (3.51) выполняют функциональное преобразование, переводящее случайный вектор огибающей U (t) из декартовой [А, В] в полярную [U, ф] систему координат (рис. 3.22, б), и вычисляют совместную плотность вероятности огибающей и начальной фазыp (U> ф). Связь между представленными координатными системами задается формулами А = Ucosy; В = t/sin ф.

При смене системы координат вероятность попадания в бесконечно малую область в окрестностях каждой точки комплексной плоскости должна остаться неизменной (площадь заштрихованного элемента на рис. 3.22, б).

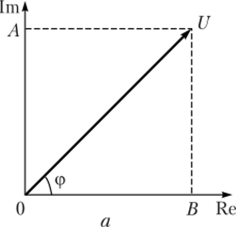
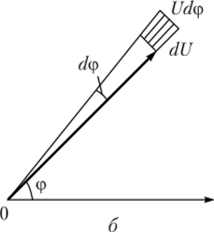
Рис. 3.22. Определение двумерной плотности вероятности комплексной огибающей:

а — квадратурных составляющих; 6 — модуля и аргумента Площадь этой бесконечно малой области в декартовых координатах выражается как dAdB, а в полярных — как UdUdy (см. рис. 3.22). Таким образом, нетрудно установить, что.

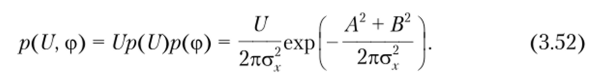
В новых переменных Л² + В² = U², поэтому двумерная плотность вероятности огибающей и начальной фазы узкополосного процесса (3.52) будет.

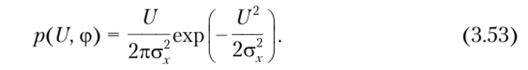
Одномерная плотность вероятности огибающей узкополосного случайного процесса. Из соотношений (3.49) и (3.53) найдем плотность вероятности огибающей:

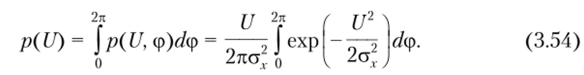
2л Поскольку p (U, ф) не зависит от начальной фазы ф = ф (?) и J dip = 2л, то о.

формула (3.54) для плотности вероятности огибающей U = U (t) упрощается:

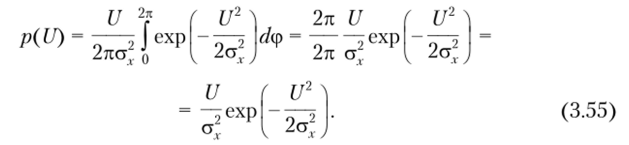
Плотность вероятности мгновенных значений огибающей узкополосного случайного процесса, описываемая законом (3.55), известна как закон (распределения) Рэлея. Приведенный на рис. 3.23 график плотности вероятности огибающей наглядно показывает, что наиболее вероятны средние значения огибающей. В то же время маловероятно, чтобы огибающая принимала значения как близкие к нулю, так и превосходящие среднеквадратический уровень а,. Максимальное значение функции p (U) получается при U = а,. Это означает, что U = а, является наивероятнейитим значением огибающей узкополосного случайного процесса.

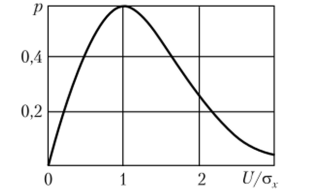
Рис. 3.23. График плотности вероятности огибающей распределенной по закону Рэлея.

Математическое ожидание огибающей узкополосного случайного процесса находим с помощью плотности вероятности (3.55):

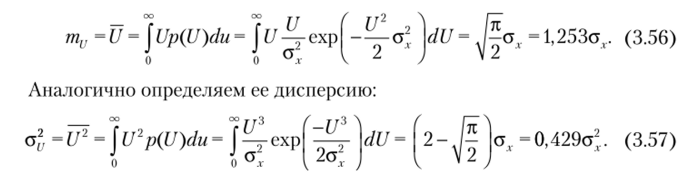
Если случайный процесс центрированный (U = 0), то из формулы (3.57) получим а₍". = 2а². Этот результат означает, что дисперсия огибающей равна удвоенной дисперсии узкополосного процесса. Это аналогично соотношению между квадратом амплитуды t/₀² и средней мощностью гармонического колебания u (t) = U₀cosa>₀t, равной u) = 0,5(см. формулу (2.70) для мощности несущей АМ-сигнала).

Располагая одномерной плотностью вероятности огибающей, можно решить ряд задач теории узкополосных случайных процессов, в частности найти вероятность превышения огибающей заданного уровня. Такой анализ проводят при исследовании процессов детектирования сигналов с шумами в приемниках.

Одномерная плотность вероятности начальной фазы узкополосного случайного процесса. Обратившись к формулам (3.50) и (3.53), найдем плотность вероятности начальной фазы, вычислив интеграл по U:

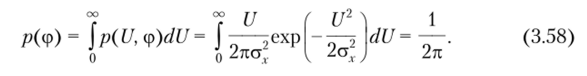
Значит, начальная фаза узкополосного случайного процесса распределена равномерно на отрезке [0, 21. Итак, мгновенное значение реализации узкополосного случайного процесса u (t) и начальная фаза cp (f) подчиняются нормальному закону, а его огибающая U (t) — закону Рэлея.

Огибающая суммы гармонического сигнала и узкополосного гауссова шума. В теории связи требуется оценить статистические свойства случайного колебания X (t), имеющего место на выходе фильтра. Пусть наряду с узкополосным нормальным шумом с центральной частотой со₀, равной резонансной частоте усилителя, на его выходе имеется гармоническое колебание u{t) = U_mcosoi₀t с амплитудой U_m. В этом случае легко найти одномерную плотность вероятности огибающей суммарного колебания. Считая, что шум задан формулой n (t) = A{t)cos (a₀t — B (?)sinсо,/, запишем выражение реализации суммарного случайного процесса X (t):

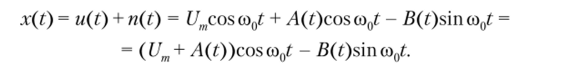
В силу узкополосности процесса х (1) любую реализацию можно выразить через медленно меняющиеся огибающую U (t) и начальную фазу ср (Г) процесса:

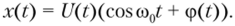
Из двух последних формул нетрудно установить, что между парами {А, В} и {U, ф} имеется такая связь: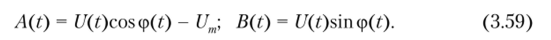

Учитывая двумерную плотность вероятности (3.51) и соотношения для квадратурных составляющих (3.59), получим в новых переменных при переходе от декартовой системы координат к полярной выражение.

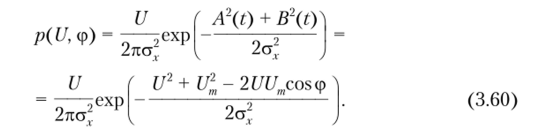
Чтобы получить одномерную плотность вероятности огибающей по формуле (3.49), следует проинтегрировать правую часть формулы (3.60) по угловой координате ф.

Для упрощения выкладок применим известную в математике формулу.

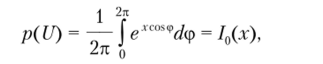
где /₀ — модифицированная функция Бесселя первого рода нулевого порядка, в результате чего получим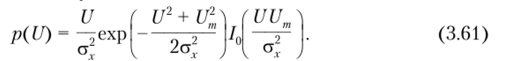

Формула (3.61) выражает распределение, получившее название закона Райса. На рис. 3.24 представлены графики плотности вероятности распределения огибающей случайного процесса, распределенной по закону Райса при различных отношениях р = U_m/a_x. Отметим, что при U_m = 0, т. е. в отсутствие детерминированного сигнала, закон Райса (3.61) переходит в закон Рэлея (3.55).

Отметим, что если амплитуда детерминированного (гармонического) сигнала значительно превышает среднеквадратический уровень шума, т. е. UJcs_x 1, то при U ~ U_m можно воспользоваться асимптотическим представлением модифицированных функций Бесселя с большим аргументом.

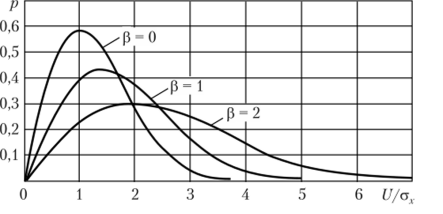
Рис. 3.24. Распределенные по закону Райса плотности вероятности случайной величины.

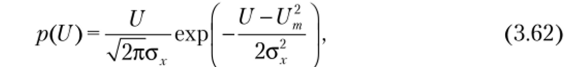
т.е. огибающая результирующего сигнала распределена в этом случае приближенно нормально с дисперсией а² и математическим ожиданием, равным амплитуде детерминированного сигнала U_m. В практических случаях считают, что уже при соотношении U_m/V = 3 огибающая суммарного колебания начинает подчиняться нормальному закону. Полезно вспомнить, что огибающая чистого шума, распределенная по закону Рэлея (3.55), имеет дисперсию а²_Г = 0,429а².