Параметрические колебания.
Динамика машин.
Колебания

В данной главе мы будем акцентировать внимание па специфических эффектах, возникающих при параметрическом возмущении, поэтому исключим из рассмотрения вынуждающие силы, вызывающие вынужденные колебания. При этом динамическая модель, приведенная на рис. 7.1, в, описывается следующим линейным однородным дифференциальным уравнением: Если считать угловую скорость двигателя со0 постоянной… Читать ещё >
Параметрические колебания. Динамика машин. Колебания (реферат, курсовая, диплом, контрольная)
Простейшие динамические модели с переменными параметрами
Как уже отмечалось в параграфе 1.3, при изменении параметров колебательной системы во времени возбуждаются так называемые параметрические колебания, которые описываются дифференциальными уравнениями с переменными коэффициентами.
Переменность параметров может возникнуть из-за изменения приведенного коэффициента жесткости, с чем мы уже сталкивались при анализе кривошипно-ползунного механизма (см. параграф 2.4). Аналогичным образом может, например, изменяться приведенная изгибная жесткость игл трикотажной и швейной машин или выдвижного шпинделя металлорежущего станка (рис. 7.1, а), поперечная жесткость направляющих шахтного подъемника и др. (рис. 7.1,6).
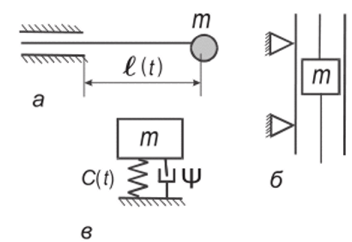
Рис. 7.1.
В подобных случаях задача сводится к анализу динамической модели, показанной на рис. 7.1,в. Нередко изменение приведенного коэффициента жесткости можно аппроксимировать гармонической функцией вида

где с0, Ас — среднее значение и амплитуда переменной части коэффициента жесткости (рис. 7.2).
Отношение? = Дс/с0 называют глубиной пульсации, период т — периодом параметрического возбуждения, а соответствующую этому периоду частоту Q = 2к/т — частотой параметрического возбуждения.

Рис. 7.2.
В данной главе мы будем акцентировать внимание па специфических эффектах, возникающих при параметрическом возмущении, поэтому исключим из рассмотрения вынуждающие силы, вызывающие вынужденные колебания. При этом динамическая модель, приведенная на рис. 7.1, в, описывается следующим линейным однородным дифференциальным уравнением:
 aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">
aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">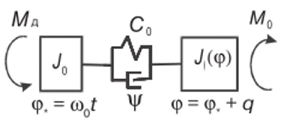
Рис. 7.3.
Источником параметрического возбуждения может также служить переменность приведенных инерционных характеристик. Рассмотрим модель упругого валопровода с переменным приведенным моментом инерции J (рис. 7.3), уравнение движения которого имеет вид.
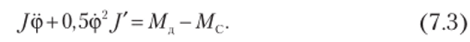
Здесь ф — абсолютная угловая координата звена приведения; М, — движущий момент; Мс — момент сопротивления; У = dj) d(р •.
Если считать угловую скорость двигателя со0 постоянной, то координата ф складывается из ф* = со/ (переносное движение) и угловой деформации q (относительное движение). Принимая во внимание, что Ma=-c0q-b0q, перепишем дифференциальное уравнение (7.3) следующим образом:

Дифференциальное уравнение (7.4) является нелинейным, так как обобщенная координата и ее производная входят в качестве аргументов нелинейных функций. Покажем, что это уравнение ценой малосущественных в динамическом отношении упрощений может быть приведено к виду линейного дифференциального уравнения с переменными коэффициентами. Разложим функции J(ф) и У'(ф) в РЯДЫ Тейлора, в которых сохраним два члена разложения.

Здесь звездочка отвечает аргументу ф, = со{)t.
Эту процедуру назовем линеаризацией в окрестности программного движения. Не следует смешивать этот прием с линеаризацией, когда нелинейная функция заменяется линейной. В данном случае относительно «большого» аргумента ф. = со0? все функции сохранили свои нелинейные свойства, и лишь малые угловые деформации q вошли в соответствующие функции линейно. Другой нелинейный фактор связан с членом (со0 + q)2, который представим как.
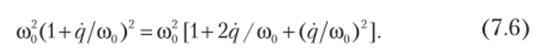
Отношение q /оо0 характеризует коэффициент неравномерности движения привода, который при нормальной работе мал и обычно нс превосходит 0,1 -г- 0,15. Легко убедиться, что последним слагаемым в квадратных скобках выражения (7.6) при этом можно пренебречь.
Подставив (7.5), (7.6) в (7.4) и исключив из рассмотрения малые нелинейные члены, получаем, что дайной модели отвечает следующее однородное линейное дифференциальное уравнение с переменными коэффициентами:
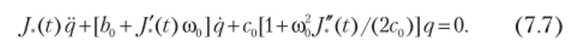
Обычно СОо/Г/(2с0) «с 1, что даст возможность дополнительных упрощений. Упрощения, связанные с линеаризацией, позволяют нам в дальнейшем пользоваться весьма важным принципом суперпозиции (см. параграф 5.8), справедливым лишь для линейных систем. В то же время, как показывает анализ, за исключением некоторых особых случаев, значения отброшенных нелинейных членов таковы, что не оправдывают дальнейших уточнений.
Итак, обобщая рассмотренные случаи, представим дифференциальное уравнение, описывающее колебательный процесс при параметрическом возбуждении, в виде.
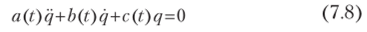
или 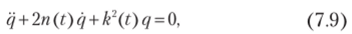
где