Метацентр, метацентрический радиус, метацентрическая высота

При наклонении корпуса изменяется форма его подводного объема, соответственно перемещается и центр величины. Рассмотрим равнообъемное накренение судна на малый угол 50 (рис. 2.2). В исходном положении судно сидело прямо, ЦВ С0 находился в ДП, в накрененном положении он сместился в точку С0. Центр кривизны дуги СОС0 — точку т0, будем называть поперечным метацентром, а ее радиус г — поперечным или малым метацешрическим радиусом.

Статический момент подводного объема V накрененного судна относительно ДП можно записать (см. рис. 2.2).

либо в виде суммы статических моментов элементарных объемов (2.4).

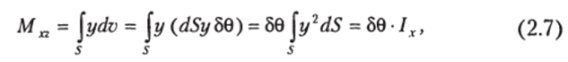
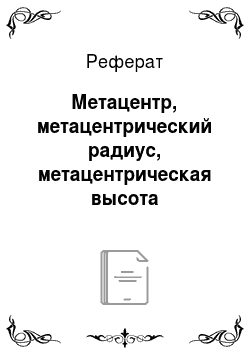
где 1_х — момент инерции площади ВЛ относительно оси накренения — оси ох.

Приравнивая (2.6) и (2.7), находим выражения для определения метацентрического радиуса:

Аналогичным образом можно получить и формулу для продольного (большого) метацентрического радиуса:

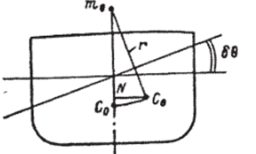
Рис. 2.2. Метацентрический радиус.

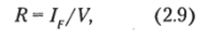
где I_F — момент инерции площади В Л относительно поперечной оси, проходящей через ее центр тяжести.

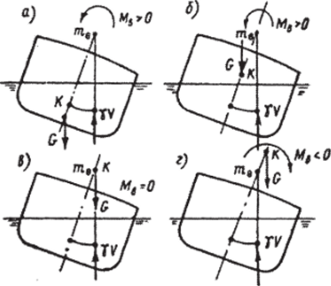
Рис. 2.3. Остойчивость судна при наклонении.

Длина судна всегда значительно больше его ширины, соответственно существенно различаются и моменты инерции 1_х и I_Fw метацентрические радиусы, поэтому один из них, поперечный, именуют малым, а второй, продольный, — большим. Соотношение этих радиусов имеет порядок (L/B)², что в точности справедливо для прямоугольного в плане понтона.

Сила плавучести всегда нормальна к плоскости ВЛ, поэтому метацентр еще можно определить и как точку пересечения линий действия сил поддержания при малом наклонении судна.

Для того чтобы судно обладало остойчивостью, его накренение должно сопровождаться появлением восстанавливающего момента. В качестве сил, создающих этот момент, выступают равные по величине силы тяжести и плавучести судна.

При фиксированном водоизмещении аппликата центра величины определяется только формой подводного объема. Возвышение центра тяжести судна за счет расположения грузов [см. (1.25)] может, вообще говоря, меняться в широких пределах. Рассмотрим четыре в принципе возможных варианта взаимного расположения ЦТ и ЦВ. В первом (рис. 2.3, а) центр тяжести лежит ниже центра величины, момент, возникающий из-за несовпадения линий действия сил тяжести и плавучести, стремится вернуть судно в положение равновесия (0 = 0), т. е. является восстанавливающим. Аналогичная картина имеет место и когда ЦТ лежит выше ЦВ, но ниже метацентра (рис. 2.3, б). В том случае, если ЦТ судна и метацентр совпадут (рис. 2.3, в), восстанавливающий момент обращается в нуль, а при дальнейшем повышении ЦТ (рис. 2.3, г) момент из восстанавливающего становится опрокидывающим — он стремится увеличить отклонение судна от положения равновесия. Говорят, что в первых двух случаях судно имеет положительную начальную остойчивость, в третьем — нейтральную, а в четвертом — отрицательную. В двух последних вариантах судно не обладает остойчивостью (см. определение этого мореходного качества).

Для надводных транспортных судов и кораблей типичным является второй вариант взаимного расположения ЦТ и ЦВ (рис. 2.3, 6). Исключение составляют только подводные лодки в погруженном положении и некоторые спортивные парусные суда.

Теперь можно объяснить понятие метацентра — в переводе с греческого слово означает «предельный центр», т. е. предельное по высоте положение центра тяжести остойчивого судна.

Мерой остойчивости судна является метацентрическая высота — расстояние между метацентром и ЦТ судна. Для малой или поперечной метацентрической высоты можно записать.

где z^, z_g, z_c — аппликаты поперечного метацентра, ЦТ и ЦВ соответственно; г — метацентрический радиус;

— возвышение ЦТ над ЦВ.

Очевидно, что аналогичные формулы можно получить и для большой (продольной) метацентрической высоты:

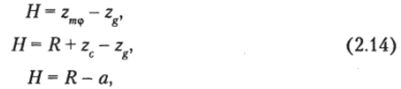
где г — аппликата продольного метацентра.

Различие между большой и малой метацентрическими высотами еще значительнее, чем между соответствующими радиусами. Так, обычно продольная метацентрическая высота существенно больше длины судна, а поперечная составляет где-то от 3 до 1% ширины (см. пример 2.1).

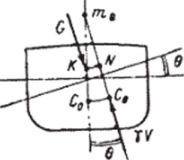
Рис. 2.4. Восстанавливающий момент.

Метацентичсские формулы остойчивости. Составляющие восстанавливающего момента. Для определения восстанавливающего момента рассмотрим накрененное на малый угол 9 судно (рис. 2.4). Плечо этого момента — расстояние между линиями действия сил тяжести и сил поддержания.

а сам восстанавливающий момент при наклонениях в поперечной плоскости.

где G — сила тяжести судна; h — малая (поперечная) метацентрическая высота.

С учетом того, что углы наклонения, рассматриваемые в начальной остойчивости, малы, запишем метацентрическую формулу остойчивости в таком виде:

Предельные значения углов крена, до которых еще справедлива метацентрическая формула (2.17), зависят от формы судна. Практика показывает, что для судов традиционной формы зависимостью (2.17) можно пользоваться вплоть до 0 * 10+12°.

Аналогичным путем получаем выражение для восстанавливающего момента в продольной плоскости:

Метацентрическая формула продольной остойчивости (2.18) применима для всех возможных в эксплуатации углов дифферента, поскольку последние обычно не превышают 3−4°.

Структура метацентрических формул остойчивости (2.17) и (2.18) показывает, что чем больше метацентрические высоты Л и Я, тем больше восстанавливающие моменты, т. е. тем сильнее судно сопротивляется наклонению. Другими словами, как уже отмечалось, метацентрические высоты суть меры начальной поперечной и продольной остойчивости. В качестве таковых еще используют произведения Gh и GH, называя их соответствующими коэффициентами остойчивости.

Записав метацентрическую высоту в форме (2.12), для восстанавливающего момента получим выражение.

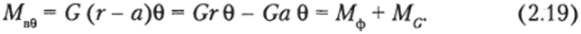
Величина метацентрического радиуса зависит только от формы судна [см. (2.8)], в связи с чем первая составляющая в (2.19) называется моментом остойчивости формы, вторая носит название момента остойчивости веса, поскольку она в значительной мере определяется положением ЦТ, но высоте [см. (2.13)]. Соответствующие названия даны и составляющим плеча статической остойчивости:

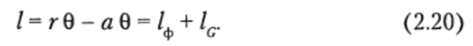
При обычном для водоизмещающих судов взаимном расположении ЦТ и ЦВ > г_с — момент остойчивости веса, а также соответствующее плечо отрицательны.

Для подводной лодки в погруженном состоянии действующая ватерлиния отсутствует: S — 0,1_х — I_f = 0, равны нулю и метацентрические радиусы [см. (2.8) и (2.9)]. Единственная возможность создать положительную остойчивость в этом случае — понизить ЦТ настолько, чтобы обеспечить z_R < z_c, а следовательно, и положительную величину момента остойчивости веса.

Этим же обстоятельством объясняется и одинаковая продольная и поперечная остойчивость подводной лодки: восстанавливающими являются только моменты веса, которые одинаковы при наклонениях в обеих плоскостях.

Метацентрические формулы остойчивости (2.17) и (2.18) находят широкое применение для определения соответствующих углов наклонения судна под действием заданного (известного) кренящего М_к или дифферентирующего М_л моментов. Действительно, статическое равновесие судна наступает при условии равенства нулю всех приложенных к нему моментов, т. е. должно иметь место.

Тогда из (2.17) и (2.21) легко находим угол крена: а из (2.18) и (2.21) угол дифферента:

На практике удобно определять угол крена, пользуясь понятием момента М°, кренящего на Г. Его легко найти по (2.17) при условии, что 0 = Г = 1/57,3:

Дифферент судна можно задать как углом ср, так и разницей осадок на носовом и кормовом перпендикулярах Д Т (см. § 1.2). Последний способ чаще применяется в судовых условиях, поскольку эксплуатационников, как правило, интересует не сам угол наклонения, а его последствия: изменение осадок носом (всхожесть на волну, слемминг и т. д.) и кормой — заглубление гребного винта. Поэтому в судовой документации, в частности на грузовой шкале (см. рис. 1.11), имеется информация о моменте М, дифферентующем судно на один сантиметр. Соответствующая формула может быть получена из (2.18) с использованием (1.1) при условии ДГ= 1 см = 0,01 м:

При наличии зависимости (2.24) угол крена судна находят по формуле

Разница осадок носом и кормой (в см) может быть определена в виде а соответствующий угол дифферента в градусах:

На практике часто используется относительный дифферент в виде.

фактический представляющий угол дифферента, измеренный в радианах.

Определить метацентрические высоты, А и Я несложно, если известно положение ЦТ по высоте z_g и имеются кривые элементов теоретического чертежа, а конкретно зависимости г, R и г. в функции от осадки (водоизмещения) судна [см. (2.11)].

На предварительных стадиях проектирования, когда теоретический чертеж еще окончательно не разработан, для оценки искомых величин можно пользоваться эмпирическими зависимостями, оперирующими главными размерениями и ограниченным количеством характеристик формы корпуса.

Так, для приближенного расчета аппликаты ЦВ предложена формула.

для малого метацентрического радиуса.

а для продольного.

Положение ЦТ по высоте в значительной степени зависит от типа и назначения судна, характера перевозимого груза, состояния загрузки и т. д.

Пример 2.1. Найдем для судна «Инженер» возвышение ЦВ, мстацентрические радиусы и высоты. Дополнительно известно z^=10,8 м.

Аппликату ЦВ определяем по (2.30):

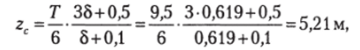
малый метацентрический радиус — по (2.31):

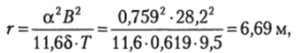
большой метацентрический радиус — по (2.32):

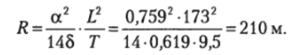
Метацентрические высоты находим с использованием (2.11) и (2.14):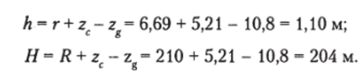

Очевидно, учитывая приближенный характер зависимости (2.32), в расчетах продольной остойчивости можно принимать // * R.

Пример 2.2. Найдем моменты — кренящий на Г и дифферентующий на 1 см.

По (2.24) имеем.

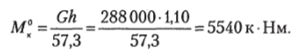
По (2.25).

Начальная остойчивость быстроходных судов.

Все высокоскоростные суда с динамическим поддержанием имеют режим плавания. Продольная и поперечная остойчивость их в этом случае принципиально ничем не отличается от рассмотренной выше: восстанавливающие моменты создаются силами плавучести и тяжести.

В расчетном режиме движения корпус этих судов выходит из воды, силы поддержания имеют динамическую природу (см. гл. 3). Эти же силы должны обеспечивать и начальную остойчивость. У глиссирующих судов при возникновении крена перераспределяются давления на скользящем по поверхности воды днище. Равнодействующая сил давления смещается от ДП в сторону накрененного борта и совместно с силой тяжести судна создает восстанавливающий момент. Аналогичная картина имеет место и у судов на неуправляемых подводных крыльях. На СПК с автоматически управляемыми подводными крыльями (АУПК) (см. гл. 3) восстанавливающий момент создается путем управления углами атаки крыльев (или закрылков). Для обеспечения поперечной остойчивости несущие крылья СПК делают разрезными в ДП с раздельным управлением закрылками правого и левого бортов.

Остойчивость СВП достигается за счет секционирования воздуш — ной подушки в продольном и поперечном направлениях. Так, например, при крене на правый борт давление в секциях, расположенных справа от ДП, возрастает, появляется восстанавливающий момент. Его увеличению будет способствовать и более интенсивный расход воздуха из подушки со стороны приподнявшегося левого борта.