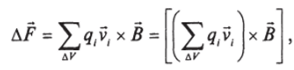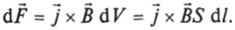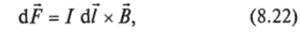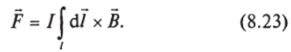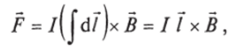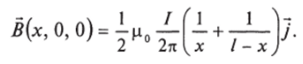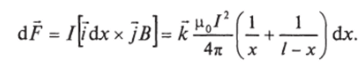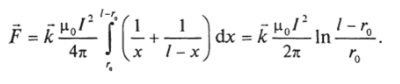Сила, действующая на ток в магнитном поле

Плотность силы

На заряженную частицу действует сила Лоренца F = qvx В. Если в объеме ДК находится большое число частиц, то на этот объем будет действовать сила ДF:

суммирование ведется по всем частицам в объеме Д V Учитывая (6.7), получаем.

Это сила, действующая на единицу объема. На отрезок проводника объемом V будет действовать сила.

Сила, действующая на линейный проводник с током

Пусть имеется тонкий проводник сечением S. На элемент проводника d/ (рис. 8.20) действует сила.

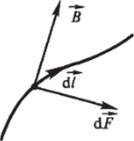
Рис. 8.20.

Напишем j 61 = j 61 и jS = /, тогда получим 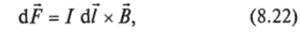и сила, действующая на кусок проводника, равна.

Какое поле должно подставляться в формулу (8.23)? По идее полное поле в точке нахождения элемента dl, т. е. поле, создаваемое внешними источниками и остальными элементами проводника. Собственное поле способно деформировать проводник. Например, при пропускании тока через замкнутый контур из гибкого проводника последний будет стремиться принять форму окружности. Однако, если мы имеем ограниченное распределение тока, собственное поле не может привести к появлению отличной от нуля результирующей силы, действующей на это распределение. Эта сила будет определяться лишь полями от внешних источников, и для ее вычисления в формулу (8.23) достаточно подставить внешнее поле.

Если поле В во всех точках проводника одинаково,.

где / — вектор, соединяющий начало и конец проводника.

Задача 8.6. Два длинных параллельных проводника соединены перемычкой (рис. 8.21). По цепи течет ток I. Какая сила действует на перемычку?

Решение. Будем считать, что проводники достаточно длинны, поэтому учитываем только поле, создаваемое этими проводниками.

Пусть перемычка ориентирована вдоль оси х. Рассмотрим элемент перемычки dx на расстоянии х от одного из проводников. В точке (х, 0, 0) поле, создаваемое двумя полубесконечными проводниками, будет (см. формулу (8.17)).

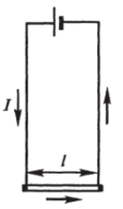
Рис. 8.21.

Сила df, действующая на элемент /dx, равна.

Полную силу найдем, интегрируя это выражение по длине перемычки. Здесь, однако, мы стал;

I

киваемся с проблемой: интеграл jdx/x на нижнем о.

пределе расходится, и сила получается бесконечной, что физически бессмысленно. Это означает, что мы неудачно смоделировали реальную ситуацию. Выход, впрочем, очевиден: нужно убрать нуль в нижнем пределе. Учтем, что всякий проводник имеет конечную толщину. Пусть проводник круглый и имеет радиус г₀. Тогда.