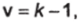Эмпирическое распределение предпочтений потребителя

Решение. Если предпочтения потребителей по отношению к товару не проявляются, то представленное в таблице распределение не должно отличаться от равномерного. Это дает основание для принятия решения применить Х²-критерий.

Поскольку отсутствие предпочтений означает равномерное распределение, то теоретической частотой для каждого выделенного класса (товара) следует считать.

где f_T — теоретическая частота; п — общее число наблюдений; к-число выделенных классов.

В нашем случае получим f_T = — = 8.

Дальнейшие расчеты осуществим в таблице 2, отражающей порядок получения эмпирической величины xLn •.

Расчет критерия х² при сопоставлении эмпирического распределения с равномерным распределением

Таблица 2

Теперь определим число степеней свободы для входа в таблицу критических значений^{-критерия} (Приложение 3):

где к- число разрядов.

В нашем случае у = 4−1 = 3, иизтаблиц находим.

Поскольку xL < Хф. ^мы вынуждены признать отсутствие предпочтений у потребителей по отношению к рассмотренной группе товаров, хотя на первый взгляд товар А был самым продаваемым.

Таким образом, данный пример показывает, что при правильной организации расчетов применение х²-критерия в определении шагов инновационного процесса не вызывает трудностей. Вместе с тем, необходимо учитывать ограничения, при которых это возможно.

1. Объем анализируемой выборки должен быть достаточно большим:

л >30.

• 2. Теоретическая частота для каждого образуемого разряда не должна быть меньше 5: f? 5. Иначе говоря, если разряды определены заранее, то необходимо «набирать» в них соответствующее число наблюдений.
• 3. Выбранные разряды должны охватывать весь диапазон вариативности изучаемого признака и совпадать во всех сопоставляемых распределениях.