Центральное растяжение-сжатие прямого стержня

Перемещения и напряжения прямого стержня при растяжении-сжатии

Рассмотрим стержень переменного поперечного сечения, полагая, что центры тяжести всех поперечных сечений лежат на прямой Ох (рис. 2.1). В соответствии с определением эта прямая является осью стержня. Стержень с прямолинейной осью принято называть прямым стержнем. Изучим возникающие в поперечных сечениях прямого стержня перемещения, напряжения и деформации, вызванные действующими вдоль его оси сосредоточенными и распределенными силами.

При расчетах будем использовать упрощающее допущение — что любое поперечное сечение при перемещении, вызванном изменением размеров стержня, остается плоским и нормальным к оси стержня. Данное предположение носит название гипотезы плоских сечений.

Воспользуемся методом сечений и определим внутренние силовые факторы, возникающие в стержне. Рассечем стержень горизонтальной плоскостью п—п, отбросим верхнюю часть стержня. Составляя уравнения равновесия (1.1) для отсеченной части, находим, что в поперечных сечениях стержня возникает только нормальная сила N (x).

Вид нагружения, при котором в поперечных сечениях стержня возникает только нормальная сила, называется растяжением-сжатием.

При расчетах воспользуемся следующим физическим правилом знаков. Сила считается положительной, если она вызывает растяжение стержня,.

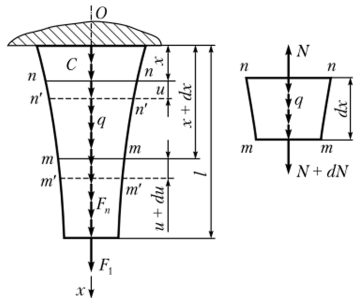
Рис. 2.1. Растяжение стержня переменного сечения и отрицательной, если в результате ее действия стержень испытывает сжатие. Данное правило будет нами также использоваться при определении знаков продольной деформации и нормального напряжения.

Выберем начало координат в точке О, в месте закрепления стержня. Под действием нагрузки поперечное сечение п—п с координатой х переместится параллельно самому себе вдоль оси стержня на некоторую величину и и займет новое положение п'—п' (см. рис. 2.1). Рассмотрим соседнее с сечением п—п сечение т—т, которое удалено от начальной точки на расстояние (х + dx). Сечение т—т, как и сечение п—п, переместится в новое положение т'—т', и его перемещение составит величину и + du.

Вычислим линейную деформацию элемента dx в направлении х как отношение удлинения этого элемента к его начальной длине:

Полученная формула дает возможность вычислить линейное перемещение любого сечения вдоль оси х.

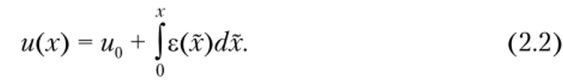
В формуле (2.2) w₀ исполняет роль постоянной интегрирования. По своему физическому смыслу величина и₀ соответствует перемещению сечения с координатой х = 0. Поскольку это сечение закреплено, и₀ = 0.

Из гипотезы плоских сечений следует, что в любой точке, принадлежащей одному и тому же поперечному сечению, линейная деформация равна одной и той же величине. Поскольку линейные деформации однозначно связаны с нормальными напряжениями, действующими в направлении х, заключаем, что эти напряжения также постоянны по сечению. Обозначая площадь поперечного сечения А (х), определяем величину напряжений по формуле.

Таким образом, использование гипотезы плоских сечений позволило нам получить закон распределения напряжений по сечению и зависимость величины нормального напряжения от величины нормальной силы в сечении.

Для определения величины нормальной силы составим уравнение равновесия элемента стержня dx (см. рис. 2.1). В сечении стержня п—п, удаленном от начальной точки на расстояние х, действует нормальная сила N. В соседнем сечении т—т, удаленном от начала координат на (х + dx), нормальная сила равна N + dN. На элемент dx стержня действует также распределенная нагрузка интенсивности q (x), равнодействующая которой составит qdx.

С учетом отмеченного уравнение равновесия запишется следующим образом:

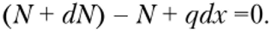
Отсюда следует дифференциальная зависимость между интенсивностью распределенных сил и нормальной силой.

Таким образом, производная от нормальной силы равна интенсивности распределенных сил, т. е. силе, приложенной к единице длины стержня, с противоположным знаком.

Установим значение нормальной силы в текущем сечении х интегрированием:

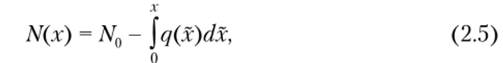
где JV₀ — постоянная величина интегрирования. Для выяснения ее физического смысла положим х = 0. Тогда из формулы (2.5) получим.

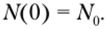
Следовательно, постоянная интегрирования N₀ в формуле (2.5) равна величине нормальной силы в начальном сечении. Отметим, что структура формулы (2.5) предполагает, что на участке от 0 до х отсутствуют сосредоточенные силы.

Таким образом, для стержня, находящегося в условиях центрального растяжения-сжатия, сначала были получены выражения линейных деформаций и перемещений, а уже после — формулы для вычисления нормальных напряжений и силы.

При получении этих формул не были использованы какие-либо дополнительные допущения о свойствах материала, что позволяет использовать их для произвольной зависимости между нормальным напряжением и линейной деформацией в =/©.

Как частный и наиболее распространенный случай рассмотрим стержень, материал которого подчиняется закону Гука. В соответствии с формулой (2.3) получим.

Если одновременно с силовой нагрузкой на величину At изменяется и температура стержня, то формула для линейной деформации получает следующий вид:

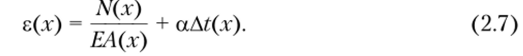
одесь, а — коэффициент температурного расширения материала.

В формулах учтено, что в общем случае величины N, Л, и At являются функциями координаты х. Что же касается Е и а, то эти величины зависят также и от температуры, о чем будет сказано далее. Примем допущение, что величины Е и, а для рассматриваемого случая расчета являются постоянными. Формула для определения перемещений произвольного сечения стержня, с учетом соотношения (2.7) приобретает вид.

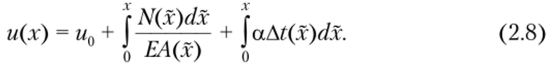
В случае если подынтегральные величины в пределах рассматриваемого участка постоянны, изменение длины этого участка Д/ вычисляется по формуле.

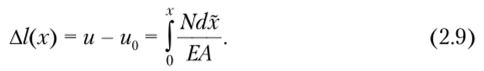
В случае нагружения стержня сосредоточенными силами следует разделить стержень на участки, в пределах которых сосредоточенные силы отсутствуют, а величины А (х) и At (x) либо постоянны, либо известен вид функции, описывающей законы их изменения.

Отметим, что величины? и, а в общем случае могут изменяться в пределах участка и к тому же модуль Е зависит от температуры. Рассмотрение подобных случаев выходит за рамки данного курса.

Уравнение равновесия удобно составлять отдельно для каждого г-го участка с использованием локальной системы координат — ж, изменяющейся от 0 до /_;, с началом в начальном сечении участка. Формула (2.8) используется для каждого участка по отдельности. При этом величина и₁₀ приобретает смысл перемещения начального сечения участка, а интегрирование проводится в пределах длины /₍ рассматриваемого участка:

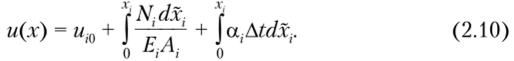
Рассмотрим прямой стержень постоянного поперечного сечения, в центре тяжести сечения С—С которого приложена сила ?(рис. 2.2).

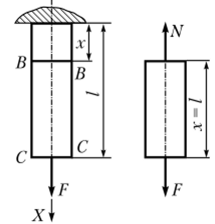
Рис. 2.2. К составлению условия равновесия.

Составим условие равновесия части тела, расположенной снизу от сечения В—В:

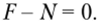
Отсюда установим значение нормальной силы N = F = const. В соответствии с формулами (2.3) и (2.10) нормальные напряжения и перемещение любого сечения определяются следующим образом:

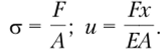
В частном случае, при х = /, получим перемещение сечения С—С, т. е. удлинение всего стержня и{1) = Д/ и.

При рассмотрении этой задачи вес тела не учитывался, поскольку предполагалось, что он пренебрежимо мал по сравнению с силой F.

Рассмотрим задачу в более точной постановке с учетом веса тела. Положим, что стержень изготовлен из материала с удельным весом у. Определим нормальную силу в сечении В—В:

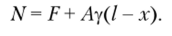
Согласно допущению о равномерном распределении напряжения нормальное напряжение в текущем сечении стержня составит.

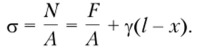
В концевых сечениях стержня величины напряжений будут равны.

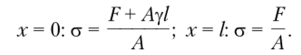
Таким образом, в случае учета веса тела нормальное напряжение зависит от координаты х и его максимальное значение имеет место в месте крепления. В этом сечении нормальная сила равна сумме приложенной силы F и веса стержня Ayl.

Для определения перемещений используем формулу (2.8):

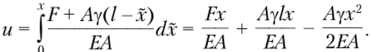
Максимальное перемещение соответствует сечению С—С и равно.

В формуле (2.12) для и второй член определяет вклад в перемещение, обусловленный собственным весом стержня. В результате решения задачи следует вывод о том, что для прямого стержня постоянного поперечного сечения, расположенного вертикально и нагруженного собственным весом, нормальные напряжения изменяются по длине.

Рассмотрим задачу равнопрочного стержня. Выясним, как должна изменяться площадь сечения вертикального стержня, находящегося под действием собственного веса и сосредоточенной силы, приложенной в нижней точке оси, чтобы нормальное напряжение в любом поперечном сечении было равно постоянной величине <�т₀.

В соответствии с заданными условиями с помощью формулы (2.3) устанавливаем значение нормальной силы:

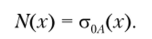
В случае когда распределенные силы представляют собой собственный вес стержня, интенсивность распределенных сил определяется следующим образом:

Учитывая соотношения (2.4), запишем дифференциальное уравнение равновесия элементарного участка стержня в виде.

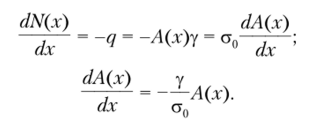
Интегрируя его, получим выражение.

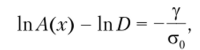
где D — постоянная интегрирования. Полученный результат перепишем следующим образом:

Для нахождения значения постоянной интегрирования D используем условие, в соответствии с которым в конечном сечении стержня С—С (/ = 0) нормальное напряжение равно <�т":

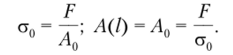
Учтем это условие в формуле (2.14):

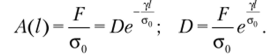
Окончательно получаем закон изменения площади поперечного сечения стержня для так называемого равнопрочного стержня, в любом поперечном сечении которого нормальные напряжения постоянны и равны ст₍₎:

Такой брус обеспечивает минимальную потребность материала п оптимален с точки зрения выполнения условия прочности.