Д. 2. 3. Изгибные колебания

Частоты свободных колебаний также рассчитываются по формуле (Д.38). Вынужденные колебания балки. Учет затухания. Для учета затухания будем предполагать, что материал балки линейно-вязкоупругий, тогда определяющее уравнение для его материала записывается следующим образом: Приведенное уравнение является уравнением движения упругой балки как континуальной системы, в которой масса распределена… Читать ещё >
Д. 2. 3. Изгибные колебания (реферат, курсовая, диплом, контрольная)
Вывод уравнения изгибных колебаний упругого стержня. Рассмотрим однородный стержень, находящийся иод действием погонной динамической нагрузки, интенсивность которой непрерывно изменяется вдоль осевой координаты и во времени (рис. Д.17).
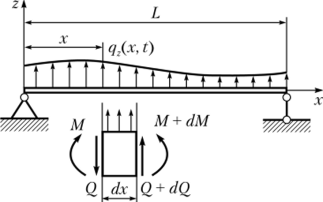
Рис. Д. 17
Предположим, что поперечные сечения балки постоянны по длине стержня.
Предположим, что во время движения каждое поперечное сечение балки совершает только малое вертикальное перемещение (v (x, t) L).
В произвольный момент движения балки мысленно вырежем бесконечно короткий элемент, действие отброшенных частей заменим внутренними силовыми факторами.
Запишем уравнение движения этого элемента:
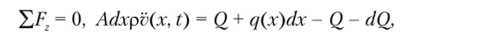
где А — площадь поперечного сечения балки; р — плотность ее материала. Учитывая, что.
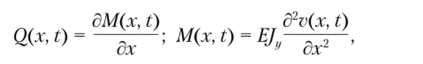
в результате получим уравнение движения упругой балки постоянного поперечного сечения.
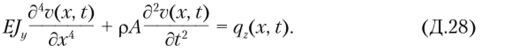
Его решение должно удовлетворять граничным и начальным условиям.
Приведенное уравнение является уравнением движения упругой балки как континуальной системы, в которой масса распределена по всему ее объему, т. е. балка рассматривается как система с бесконечным числом степеней свободы. Это уравнение описывает незатухающие колебания.
Свободные колебания упругой балки. Собственные динамические характеристики. Если на балку не действуют внешние силы, то в уравнении (Д.28) нагрузка qx.= 0 и она совершает свободные колебания, которые описываются следующим уравнением:
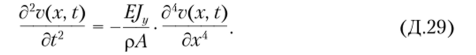
Решение разыскивается в виде бесконечного ряда, каждый член которого представляет собой произведение двух функций, одна из которых является функцией только координаты х, а вторая — только времени t

Каждый член ряда должен удовлетворять уравнению движения (Д.29) и граничным условиям; весь ряд (вся сумма) должен удовлетворять также начальным условиям.
Подставим выражение (Д.ЗО) в уравнение (Д.29) и, требуя удовлетворения исходного уравнения каждым членом ряда, для каждого номера п получим.
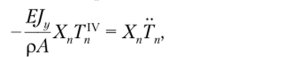
где римской цифрой обозначена производная по координате, а точками производная по времени.
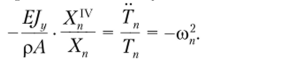
Это равенство можно переписать в следующем виде:
Здесь (о%, п = 1, 2, 3,…, — произвольные константы. Из этого равенства следует два уравнения.

где Таким образом, применение метода разделения переменных дало возможность вместо интегрирования уравнения в частных производных (Д.29) искать решение двух обыкновенных дифференциальных уравнений (Д.31) и (Д.32).
Интегралы этих уравнений известны. Если со" = 0 и стержень свободен от закреплений, то эти уравнения описывают его апериодическое движение как жесткого тела. Этот случай рассматривать не будем.
При со, ^ 0 получаем решения, описывающие изгибные колебания балки:
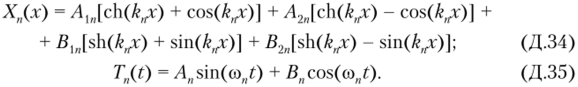
Здесь Аи, Л2п, В,я, В2п, ооп — произвольные постоянные, которые находятся из граничных условий.
Балка, шарнирно опертая по концам. В этом случае в крайних сечениях балки должны отсутствовать прогибы и изгибающие моменты, поэтому граничные условия имеют вид.
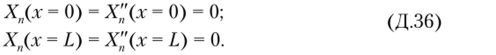
Из первых двух граничных условий (Д.36) следует, что Д|н = А.,п = 0. С учетом этого решение (Д.34) и его первые две производные запишутся следующим образом:
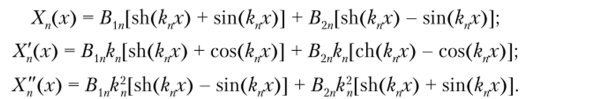
Из других граничных условий (Д.36) следует, что 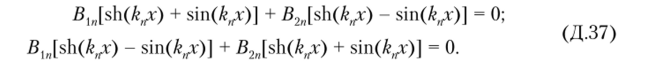
Тривиальное решение этой системы уравнений (В1п = В2п = 0) должно быть отброшено, так как в этом случае будут отсутствовать деформации изгиба, что противоречит исходному предположению.
Условием существования нетривиального решения системы является равенство нулю ее определителя, т. е.
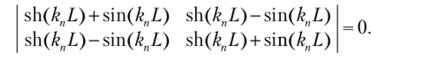
Раскрывая его, получаем частотное уравнение.
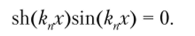
Если kn f* 0 (а сейчас рассматривается именно этот случай), то sh(knL) * 0 и, следовательно, необходимо потребовать, чтобы sin(knL) = 0. Это возможно при knL = пп (и = 1, 2,…).
Отсюда kn = пк/L и, учитывая равенство (Д.ЗЗ), найдем выражение для круговых частот изгибных колебаний балки:
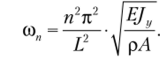
Так как sin(knL) = 0, то из уравнений (Д.51) следует, что BUl = -В2п и выражение для координатной части решения запишется в виде.
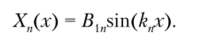
Здесь Ви — подлежащие определению константы.
Таким образом, граничные условия дали возможность найти частоты и формы изгибных колебаний балки, т. е. се собственные динамические характеристики.
На рис. Д. 18 схематично показаны первые три формы изгибных колебаний рассматриваемой балки.
Таким образом, решение задачи о свободных колебаниях шарнирно опертой по концам балки примет вид.
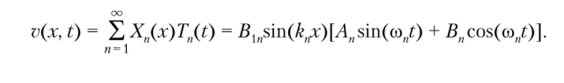
Используя начальные условия и свойство ортогональности собственных форм, можно найти константы:
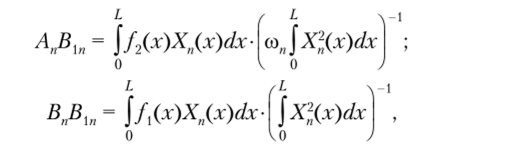
где /,(х) — начальные перемещения сечений балки; /2(ж) — начальные скорости этих перемещений. Эти функции считаются заданными.
Приведем без вывода частотные уравнения и частоты свободных колебаний балок при других условиях закрепления их концов.
Консольная балка. Предположим, что левый торец балки заделан, а правый свободен. В этом случае.
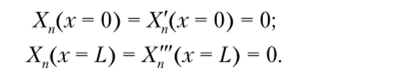
Частотное уравнение имеет вид 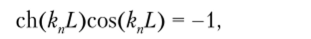
а первые шесть его корней равны.
k, L | k, L | k., L | KL | kr, L | KL |
1,875. | 4,694. | 7,855. | 10,996. | 14,137. | 17,279. |
Частоты свободных колебаний рассчитываются по формуле 
Балка с заделанными концами. В этом случае Частотное уравнение имеет вид.
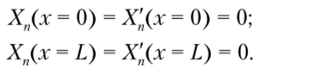
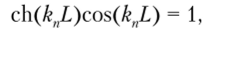
k{L | k., L | k, L | k, L | k5L | KL |
4,730. | 7,853. | 10,996. | 14,137. | 17,279. |
Частоты свободных колебаний рассчитываются по формуле (Д.38). Балка, один конец которой заделан, а второй шарнирно оперт. В этом случае.
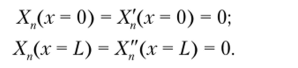
Частотное уравнение имеет вид 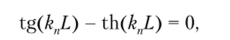
а первые шесть его корней равны.
k, L | k, L | k, L | KL | k-L | kKL |
3,927. | 7,069. | 10,210. | 13,352. | 16,493. | 19,634. |
Частоты свободных колебаний также рассчитываются по формуле (Д.38). Вынужденные колебания балки. Учет затухания. Для учета затухания будем предполагать, что материал балки линейно-вязкоупругий, тогда определяющее уравнение для его материала записывается следующим образом:
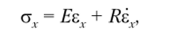
где R — коэффициент вязкости материала.
Будем предполагать, что бачка нагружена погонной нагрузкой, интенсивность цг{х, t) которой задана.
Повторяя выкладки, приведенные при выводе уравнения продольных колебаний упругого стержня, можно получить уравнение вынужденных колебаний балки с учетом затухания в виде.
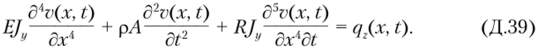
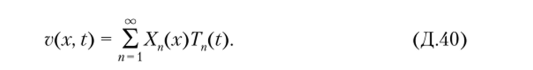
Решение этого дифференциального уравнения в частных производных будем искать методом разделения переменных, представляя его решение в виде ряда К ряду предъявляются такие же требования, как и при решении задачи о продольных колебаниях стержня.
Внешнюю нагрузку представим в виде произведения двух функций, т. е.
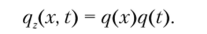
Координатную часть ее также разложим в ряд по собственным формам, т. е.
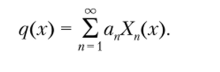
Коэффициенты этого разложения находят, используя свойство ортогональности собственных форм, они оказываются равными.
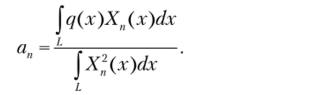
Таким образом, окончательно внешнюю нагрузку представим следующим разложением:

Подставляя выражения (Д.41) и (Д.40) в уравнение (Д.39), получим.
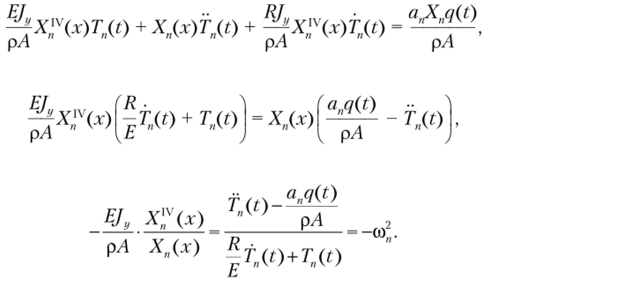
или или Здесь со, — константы, смысл которых будет определен ниже. Отсюда следует, что.
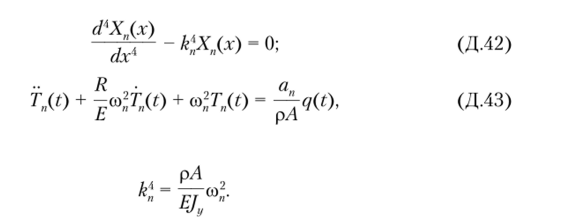
где Как видно, уравнения (Д.42) описывают координатную часть решения.
Временная часть решения находится интегрированием уравнения (Д.43), которое идентично соответствующему уравнению продольных колебаний стержня. Поэтому все решения, рассмотренные в подпараграфе Д. 2.1, переносятся на рассматриваемый случай изгибных колебаний балки.
Интегрирование уравнений в частных производных является сложной математической задачей, поэтому они используются довольно редко.
Если поперечное сечение балки переменно по ее длине или материал неоднороден, то уравнение движения будет содержать переменные коэффициенты и его интегрирование еще больше усложняется. Поэтому в большинстве практически важных случаев прибегают к дискретной модели, в которой массу балки сосредоточивают в нескольких ее сечениях. Таким образом, балка представляется системой с конечным числом степеней свободы и ее движение описывается системой обыкновенных дифференциальных уравнений, интегрирование которых с использованием компьютера не представляет принципиальных трудностей.