Доверительные интервалы. 
Политический анализ и прогнозирование в 2 ч. Часть 2

В главе 3 мы рассматривали вопрос о различиях между параметрами генеральной совокупности и их статистическими оценками. Первые представляют собой, как правило, неизвестные и детерминированные (закономерные) величины, вторые — известные случайные величины. Таким образом отличаются, например, математическое ожидание величины от среднего арифметического, теоретическая дисперсия — от оценки дисперсии. Однако до сих пор мы ограничивались только одним, хотя и очень важным типом статистической оценки параметров — точечной оценкой. Точечная оценка представляет собой одно число — среднее арифметическое, или дисперсию, или стандартное отклонение. Существует и другой способ оценить параметр генеральной совокупности — показать, в каком интервале значений он содержится с установленной вероятностью. Такая оценка называется интервальной оценкой.

Например, нас интересует средний возраст сторонников некоторой политической партии А. Это — параметр генеральной совокупности, включающей в себя всех сторонников этой партии. Практически наверняка оценивать этот параметр придется по некоторой ограниченной выборке объема п. Допустим, имеются следующие данные, сведенные в табл. 5.4: в нечетных столбцах указаны номера наблюдений (респондентов), в четных — возраст респондента в годах (А).

Таблица 5.4

Чтобы получить точечную оценку, мы просто подсчитаем среднее арифметическое: суммируем все отдельные значения переменной «возраст членов партии» (А) и разделим на объем выборочной совокупности. В результате мы сможем выяснить, что средний возраст членов партии А составляет 43 года. Однако этот замечательно простой способ обладает одним очень существенным недостатком: мы не знаем, насколько точной является полученная оценка. Иначе говоря, мы не знаем, в какой мере она может отклоняться от истинного среднего генеральной совокупности. И в этой ситуации нам на помощь приходит интервальная оценка. Она позволит нам утверждать, например, следующее: «Мы на 0,95 (или на 95%) уверены, что средний возраст членов партии А находится между 38 и 48 годами».

Первое, что необходимо сделать для расчета интервальной оценки, — определиться с доверительным уровнем¹ (confidence level). Доверительный уровень представляет собой вероятность того, что оцениваемый интервал будет содержать искомый параметр. По существу, доверительный уровень отражает степень нашей уверенности в полученном результате. В статистике обычно используются три основных доверительных уровня: 0,9, 0,95 и 0,99. Далее мы будем работать преимущественно с доверительным уровнем 0,95 (если специально не оговорено иное). В большинстве статистических программ именно такая величина доверительного уровня используется по умолчанию.

'Также используется понятие «доверительная вероятность».

Доверительным уровням соответствуют уровни статистической значимости а («альфа-уровни»). Уровень значимости дополняет доверительный уровень до 1:

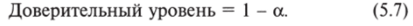
Содержательно уровень значимости показывает, с каким риском ошибки мы готовы смириться. Принятие доверительного уровня 0,95 означает, что в 5 выборках из 100 (а = = 1 — 0,95 = 0,05) рассчитанный интервал не будет накрывать истинный параметр. Так, на рис. 5.15 один из интервалов не содержит искомую величину.

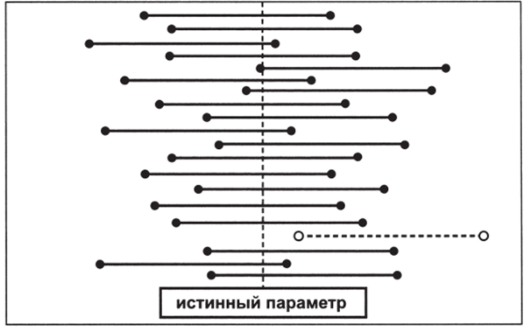
Рис. 5.15.

Выше мы привели пример утверждения относительно интервала, содержащего средний возраст членов партии А. Формальная запись того же самого утверждения следующая:

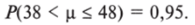
Для практической работы по определению доверительных интервалов нам потребуется стандартное нормальное распределение. Прежде всего, определим z-значения, соответствующие выбранному нами доверительному уровню 0,95. Раньше мы сопоставляли вероятности известным z-значениям; теперь требуется решить обратную задачу. Воспользуемся для этого имеющейся в Excel функцией.

«=НОРМСТОБР»; ее единственным аргументом является вероятность.

Но какую вероятность следует задать? Напрашивающийся ответ «0,95» является неверным. Обратите внимание, что соответствующая вероятности 0,95 площадь находится в центре распределения; следовательно, «остаток» площади I — 0,95 = 0,05 должен быть поровну распределен между «хвостами». Это показано на рис. 5.16.

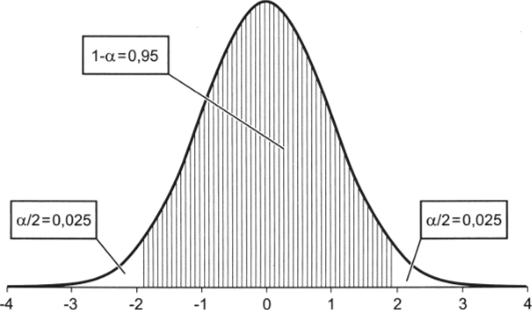
Рис. 5.16.

Следовательно, верхняя граница интервала должна быть задана на основе вероятности 0,95 + 0,025 = 0,975 (рис. 5.17).

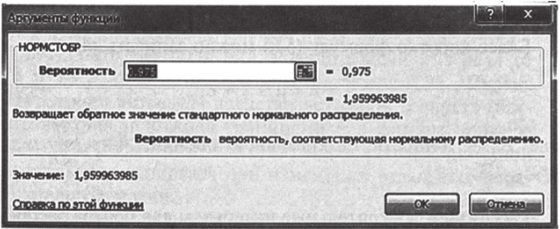
Рис. 5.17.

Округленное z-значение составляет 1,96.

В табл. 5.5 приведены г-значения, соответствующие основным доверительным уровням (далее мы будем обозначать их z_a).

Таблица 5.5

Сначала рассмотрим расчет доверительного интервала для ситуаций, когда выборка сравнительно велика (я > 30) и/или стандартное отклонение для генеральной совокупности известно. В этих случаях доверительный интервал определяется по следующей формуле:

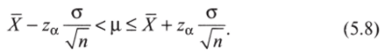
В этой формулеiявляется стандартной ошибкой средня него (глава 3). Если стандартное отклонение генеральной совокупности неизвестно, вместо о используется оценка стандартного отклонения S_x. Здесь следует отметить, что для анализа данных в политической науке обычной ситуацией является отсутствие информации об истинном значении стандартного отклонения генеральной совокупности. Поэтому, по существу, практическое значение имеют два сценария: 1) выборка сравнительно велика; 2) выборка мала.

Более коротко формулу (5.8) можно записать так:

где Е — точность интервальной оценки, Е = z_a -4L или.

E = z

yjn

Рассчитаем доверительные интервалы для центра распределения на основе данных в табл. 5.4, объем выборки составляет 32. Данные в электронном виде доступны по ссылке http://polit.msu.ru/kaf/lab_quant/.

Упражнение 5.2

• 1. Рассчитайте среднее арифметическое X и стандартное отклонение S_x.
• 2. Укажите в соответствующих ячейках объем выборки п и значение z_a, соответствующее доверительному уровню 0,95 (1,96).
• 3. Рассчитайте v", стандартную ошибку среднего, точность оценки Е (соответствующие функции имеются на рис. 5.18).
• 4. Рассчитайте нижнюю границу доверительного интервала, вычтя значение Е из среднего арифметического.
• 5. Рассчитайте верхнюю границу доверительного интервала, прибавив Е к среднему арифметическому.

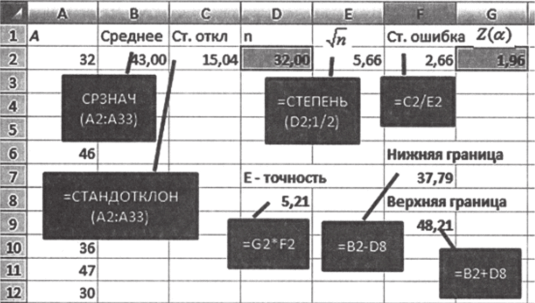
Рис. 5. IS

В результате мы получили доверительный интервал от 37,79 до 48,21 года на доверительном уровне 0,95. Ширина доверительного интервала представляет собой разность между его верхней и нижней границами и в данном примере равна 10,42. Посмотрим, что будет происходить с шириной доверительного интервала при изменении отдельных параметров нашей задачи.

• 6. Перейдем к доверительному уровню 0,9. В табл. 5.5 z_a для этого уровня составляет 1,64. Введите это значение в соответствующую ячейку. Новые границы равны 38,64 и 47,36, ширина интервала — 8,72.
• 7. Перейдем к доверительному интервалу 0,99; z_a = 2,58. Введите это значение в нужную ячейку. Новые границы — 36,14 и 49,86, ширина интервала 13,72.

Таким образом, при повышении доверительного уровня I — а при прочих равных условиях происходит увеличение ширины доверительного интервала и, соответственно, снижение точности оценки. Чем шире доверительный интервал, тем меньшей практической полезностью он обладает. Вы можете испытывать исключительно сильную уверенность в том, что истинное значение температуры воздуха за окном находится между -20 °С и +20 «С, но это не поможет вам выбрать подходящую одежду. С другой стороны, чрезмерное сужение доверительного уровня сильно увеличивает наши риски, а статистическое оценивание — это не игра в рулетку. Так, чтобы в нашем примере уменьшить ширину доверительного интервала до 3,5 лет, мы были бы вынуждены смириться с 50%-й вероятностью ошибки, что совершенно неприемлемо. Практически, реальный выбор доверительного уровня происходит именно в том диапазоне, который зафиксирован в табл. 5.5: от 0,9 до 0,99.

Единственный способ добиться большей точности интервальной оценки при сохранении доверительного уровня — увеличить объем выборки. Продолжим выполнение упражнения 5.2.

• 8. Вернемся к доверительному уровню 0,95. Введите соответствующее ему значение z_a в нужную ячейку.
• 9. Увеличим в два раза объем выборки: с 32 до 64 (допустим, что у нас появилось больше данных). В результате нижняя граница доверительного интервала составляет 39,31, верхняя — 46,69, ширина — 7,37. В данном случае двукратное увеличение выборки позволило нам сократить ширину доверительного интервала примерно на треть.

Действительно, увеличение объема выборки всегда приводит к увеличению точности интервальной оценки. Но при этом эффект увеличения объема выборки будет значительным для выборок малого и среднего размера. С ростом п приращение точности будет происходить все более медленными темпами.

10. Будем каждый раз удваивать объем выборки, сохраняя при этом получившееся значение ширины доверительного интервала. В результате появится табл. 5.6.

11. Используя эти данные, построим график зависимости ширины интервала от объема выборки. Для этого воспользуйтесь опцией «Вставить диаграмму — точечную — точечную с гладкими кривыми» (см. рис. 5.19).

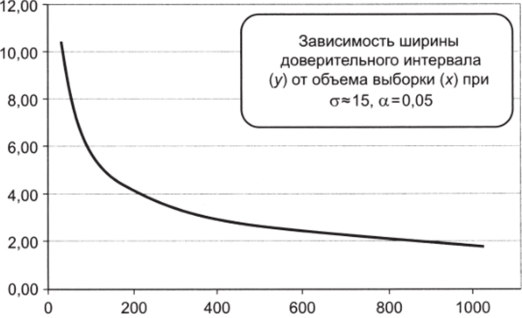
Рис. 5.19.

На рисунке видно, что с увеличением выборки, начиная с определенных значений п, выигрыш в точности — сокращение ширины доверительного интервала — начинает резко уменьшаться. Конкретная форма такой зависимости будет различаться для разных доверительных уровней и разных показателей вариации переменной, но ее принципиальный вид останется неизменным. Практически это означает, что не имеет смысла стремиться к формированию очень больших выборок: прирост в точности попросту «не окупит» дополнительных затрат ресурсов. Именно поэтому при проведении, например, массовых социологических опросов выборка составляет не более 1500−2000 респондентов.

Выполнение упражнения 5.2 позволило нам по шагам рассмотреть расчет доверительных интервалов для выборок.

n > 30. Ускоренное построение доверительного интервала в Excel осуществляется с помощью функции «=ДОВЕРИТ».

Ее аргументами являются: уровень значимости а. стандартное отклонение и объем выборки (см. рис. 5.20).

Рис. 5.20.

Обратите внимание, что функция «=ДОВЕРИТ» возвращает точность интервальной оценки Е. Чтобы получить доверительный интервал, необходимо самостоятельно подсчитать X ± Е для определения верхней и нижней границы.

Следующий практически важный вопрос заключается в том, как рассчитать доверительный интервал для малой выборки (п < 30). В политических исследованиях совокупности такого объема встречаются очень часто.

Если истинное значение стандартного отклонения о в генеральной совокупности было бы известно, мы воспользовались бы той же процедурой, что и для выборок большего размера. Однако в анализе политологических данных истинная вариация почти всегда неизвестна. Поэтому мы будем исходить из сочетания малого объема выборки и неизвестного о.

Это сочетание порождает два новых для нас обстоятельства.

• • Мы вынуждены явным образом делать предположение о том, что изучаемая совокупность является нормально распределенной. Это происходит потому, что при п < 30 перестает работать в полном объеме центральная предельная теорема. Напомним, ее замечательное следствие заключается в том, что распределение выборочных средних будет нормальным даже тогда, когда сами выборки извлечены из ненормально распределенных совокупностей.
• • Стандартное нормальное распределение, использовавшееся нами при определении z_a, перестает быть надежным подспорьем для расчета доверительных интервалов. При малых выборках стандартное нормальное распределение дает слишком узкие интервалы; следовательно, возникает угроза систематического завышения точности интервальной оценки. Поэтому при малых выборках мы будем использовать другой закон распределения — распределение Стьюдента.

Распределение Стьюдента (/-распределение) имеет ряд общих черт со стандартным нормальным распределением (z-распределением): оно симметрично относительно центра и имеет колоколообразную форму. При этом оно является более «плоским» или «пологим»: стандартное отклонение /-распределения больше единицы. Ключевое же отличие состоит в том, что основным управляющим параметром распределения Стьюдента является число степеней свободы.

В разных науках это понятие определяется по-разному. Например, в физике число степеней свободы — это минимальное количество параметров, требуемых для полного описания физической системы. Определение, которое мы дадим здесь, не вполне строгое; в то же время оно будет достаточным для наших задач. Итак, число степеней свободы — это количество случайных величин, которые должны принять определенные значения, чтобы все интересующие нас величины приняли определенные значения. Например, известно, что х + у + z = 100, т. е. сумма трех чисел равна 100. Сколько переменных должны принять определенные значения, чтобы все значения были нам известны? Таких переменных две: как только известны значения х и у_у мы сможем найти z = 100 — (х + у). Число степеней свободы в данном примере — 2.

Другой пример. Пусть требуется рассадить трех человек (А, В, Q на трех стульях (Д Е, F), математически — поставить в соответствие каждому элементу множества из трех людей элемент из множества трех стульев. Такое соответствие будет определено, как только будут рассажены два человека. Если известно, что А сидит на стуле Д, а В — на стуле ?, становится ясно, что С займет стул F. У рассаживающего просто нет других вариантов, его «свобода» исчерпана. Вновь число степеней свободы равно 2.

Для одномерных распределений (отдельных переменных) число степеней свободы (обозначается df от английского.

«degrees of freedom») рассчитывается по очень простой формуле:

где п — общее число наблюдений.

Каждому числу степеней свободы df в распределении Стьюдента соответствует своя колоколообразная кривая. Чем больше df, тем менее пологим является распределение и тем ближе оно к z-распределению. На рис. 5.21 схематично показано, как с ростом числа степеней свободы происходит сближение двух законов распределения.

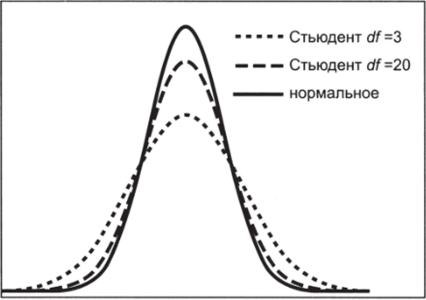
Рис. 5.21.

При объеме выборки в 30 и более элементов эти распределения становятся практически идентичными. В этом определенное преимущество /-распределения перед z-распределением: первое годится для работы с выборками любого объема, второе — только для сравнительно больших выборок.

Математически распределение Стьюдента значительно сложнее z-распределения. Мы не приводим здесь его интегральную и дифференциальную функции, и нам было бы довольно трудно получить /-значения «вручную», как это было сделано для нормального распределения. Поэтому мы ограничимся работой с таблицей распределения Стьюдента; здесь приводится ее сокращенный вариант (табл. 5.7).

В столбцах полужирным шрифтом выделены степени свободы, в строках — доверительные уровни. На пересечении строк и столбцов приведены /-значения, или критические значения /-распределения Стьюдента (будем обозначать их /_а). Именно их использование и отличает механизм расчета интервальной оценки среднего для малых совокупностей от того, что мы делали раньше с использованием z-значений.

Формула расчета доверительного интервала для выборок объема п < 30 такова:

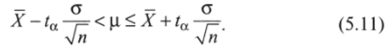
Эта формула очень похожа на формулу (5.8). Таким образом, полностью в силе остается общий подход к определению доверительного интервала: X — Е < р < X + Е. Только теперь для расчета точности оценки Е используется /_а вместо z_a.

Для отработки интервальной оценки среднего с использованием распределения Стьюдента вернемся к данным в табл. 5.4. Только теперь ограничимся первыми 20 наблюдениями.

Упражнение 5.3

• 1. Рассчитайте среднее арифметическое X и стандартное отклонение S_x. Они будут равны 38,55 и 12,77 соответственно.
• 2. Укажите объем выборки п (20).

зз.

• 3. Рассчитайте число степеней свободы, оно равно п — — 1 = 20 — 1 = 19.
• 4. Найдите по табл. 5.7 значение /_а, соответствующее доверительному уровню 0,95 (рис. 5.22).
• 1_а = 2,093 (обратите внимание, что оно несколько больше z_a для того же самого доверительного уровня). Введите его в соответствующую ячейку.

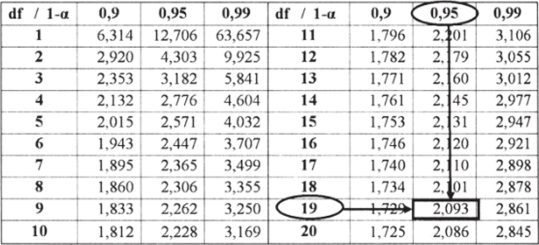
Рис. 5.22

5. Рассчитайте V", стандартную ошибку среднего, точность оценки? (соответствующие функции имеются на рис. 5.23).

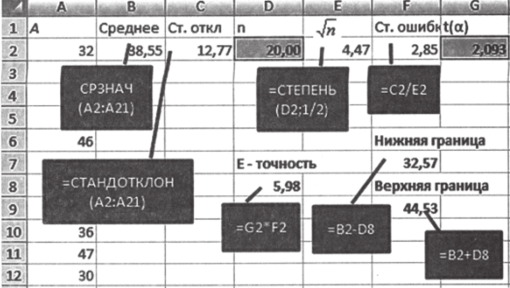
Рис. 5.23.

• 6. Рассчитайте нижнюю границу доверительного интервала, вычтя значение? из среднего арифметического.
• 7. Рассчитайте верхнюю границу доверительного интервала, прибавив Е к среднему арифметическому.

Итак, нижняя граница доверительного интервала составляет 32,57, верхняя — 44,53, широта интервала — 11,95.