Измерение силы связи категориальных переменных

В этом разделе мы будем рассматривать переменные, измеренные на номинальном уровне, а также порядковые переменные с небольшим числом категорий. Допустим, нас интересует статистическая связь между степенью удовлетворенности респондента политикой, проводимой правительством (S), и его политической ориентацией (Р). Удовлетворенность политикой, проводимой правительством, в нашем примере будет порядковой переменной с тремя значениями: «совершенно неудовлетворен» (У,), «частично удовлетворен» (5₂), «полностью удовлетворен» (5₃). Политическая ориентация будет номинальной переменной с двумя значениями: «консервативная» (Д,) и «либеральная» (Р₂). Матрица сопряженности этих признаков (обозначим ее а₀) приведена в табл. 8.11.

Таблица 8.11

Измерить силу статистической связи между этими переменными можно, руководствуясь двумя основными стратегиями. Первая основана на расчете критерия хи-квадрат (X²); вторая — на расчете показателя лямбда (А.).

Идея, лежащая в основе вычисления критерия хи-квадрат, заключается в сравнении эмпирической матрицы сопряженностей, А с такой теоретической матрицей А', для которой статистическая связь отсутствует. Другими словами, мы сравниваем имеющееся распределение частот с таким распределением, где сила связи гарантированно равна нулю. Чем сильнее отличие реальной матрицы от теоретической, тем сильнее статистическая связь.

Тестируемая нулевая гипотеза такова:

Она эквивалентна утверждению об отсутствии связи между переменными. Альтернативная гипотеза содержит противоположное утверждение.

Расчет матрицы A' = a’j мы рассматривали выше (8.7). Чтобы получить частоты, гарантирующие отсутствие связи, нужно умножить сумму в строке, в которой находится элемент, на сумму в соответствующем столбце, а затем разделить на общую сумму частот. Произведем расчет для нашего примера (это удобно делать в программе Excel):

Итак, получена теоретическая матрица сопряженностей, в которой изменение значений одной переменной не приводит к изменению условного распределения вероятностей другой переменной (см. табл. 8.12). Сила статистической связи между переменными равна нулю.

Таблица 8.12

Теперь, в соответствии с логикой критерия у}, следует сравнить наблюдаемые и теоретические частоты. Математически такое сравнение будет заключаться в вычитании теоретических частот из эмпирических, a_tj — а, у. В статистике разность между наблюдаемым и теоретическим значениями называется остатком. Для нашего примера остатки получаются следующие: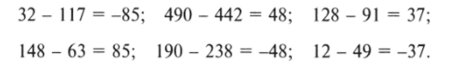

Далее требуется получить одно определенное число, характеризующее различия между двумя матрицами. Складывать их бесполезно, так как сумма остатков всегда равна нулю; положительные остатки «гасят» отрицательные. Поэтому сначала необходимо возвести все остатки в квадрат и разделить на теоретические частоты я'. Последняя операция называется нормировкой; она нужна для того, чтобы критерий не был чувствителен к числу наблюдений (абсолютным частотам):

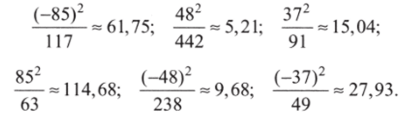
Теперь полученные числа суммируются: 61,75 + 5,21 + + 15,04 + 114,68 + 9,68 + 27,93 = 234,31. Мы получили значение х². Общая формула критерия такова:

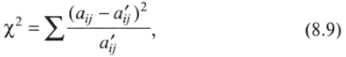
где a’j = ===—.

Для примера с удовлетворенностью политикой правительства и идеологической ориентацией получен %²~ 234,31. Но как интерпретировать это число в терминах наличия или отсутствия связи? Нам вновь понадобятся критические значения, следовательно — специальное распределение. Это распределение Хи-квадрат, управляющим параметром которого является число степеней свободы.

Мы уже обращались к понятию степеней свободы при изучении распределений Стьюдента и Фишера. Напомним, что число степеней свободы — это количество случайных величин, которые должны принять определенные значения, чтобы все интересующие нас величины приняли определенные значения. Для одномерных распределений число степеней свободы задается формулой df = п — 1, где п — общее число наблюдений.

Но в задаче измерения силы связи между переменными нас интересует число степеней свободы их совместного распределения; иначе говоря, нас интересует число степеней свободы матрицы сопряженностей. Матрица — двумерный объект, где каждый элемент имеет две «координаты» — номер строки и номер столбца. В этой связи формула для числа степеней свободы матрицы, содержащей т строк и п столбцов, будет чуть сложнее:

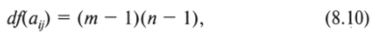
т.е. требуется вычесть по единице из числа строк и из числа столбцов и перемножить результаты. Так, в матрице 2×2 всего одна степень свободы:

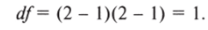
Действительно, достаточно задать любой элемент такой матрицы, чтобы рассчитать все остальные. Предполагается, что все суммарные показатели нам известны (см. рис. 8.11).

Рис. 8.11.

В примере с поддержкой правительства матрица имеет размер 2×3. Следовательно, число степеней свободы составляет df= (2 — 1)(3 — 1)=2.

Распределение Хи-квадрат, как и распределение Фишера, обладает положительной асимметрией. При увеличении числа степеней свободы оно становится все более симметричным, и в этом также проявляется сходство с^{-распределением} (см. рис. 8.12').

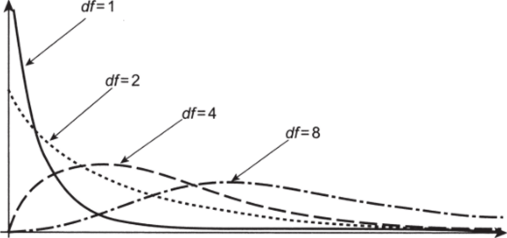
Рис. 8.12.

Имеется специальная таблица критических значений у}, фрагмент которой приведен ниже (см. табл. 8.13).

Таблица 8.13

Нулевая гипотеза (8.8) содержит утверждение о равенстве эмпирической матрицы ожидаемой при отсутствии связи. Чтобы нулевая гипотеза была отвергнута на определенном уровне статистической значимости, требуется, чтобы эмпирическое значение было больше критического:

Напомним, что для случая с переменными «поддержка политики правительства» и «политическая ориентация» число степеней свободы составляет 2. Находим в табл. 8.13 соответствующую строку. Пусть уровень статистической значимости составляет 0,001 (это последний столбец в таблице). Критическое значение равно 13,815 (см. рис. 8.13).^[1]

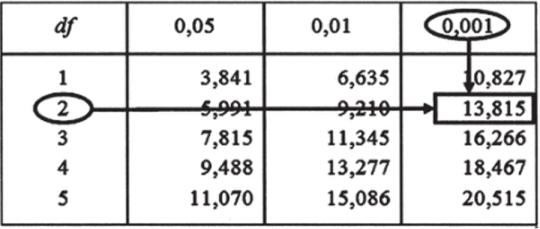
Рис. 8.13.

Так как расчетное значение хи-квадрат значительно больше критического — 234,31 > 13,815, нулевая гипотеза отвергается и принимается альтернативная гипотеза о наличии связи между переменными.

Как обычно, вместо таблицы мы можем воспользоваться функцией в программе Excel: «=ХИ20БР». Ее аргументами являются:

• • вероятность — уровень статистической значимости;
• • степени свободы — число степеней свободы.

Рис. 8.14

Чтобы получить наблюдаемый уровень значимости, или /^-значение, можно воспользоваться функцией «=ХИ2РАСП». Ее аргументами являются значение хи-квадрат и число степеней свободы (см. рис. 8.15).

Рис. 8.15.

Получается число со многими нулями после запятой. Вероятность отвергнуть истинную нулевую гипотезу об отсутствии связи микроскопически мала, и мы уверенно принимаем альтернативную гипотезу о наличии связи между переменными.

Вместе с тем этот ответ не полностью соответствует поставленной задаче: мы ведь хотели получить числовую характеристику силы связи, а не только утвердиться в уверенности, что она существует. Существует несколько практических способов получить оценку силы связи на основе у}. Достоинство всех приводимых ниже коэффициентов состоит в том, что они стандартизированы: в отличие от х², они принимают значения от 0 до 1. Близость к 1 означает сильную связь, близость к 0 — слабую связь или ее отсутствие.

1. Коэффициент сопряженности Пирсона (с):

где /V — общая сумма частот в матрице сопряженностей.

У коэффициента сопряженности два недостатка. Первый состоит в том, что его значение никогда не достигает единицы. В формуле (8.12) числитель всегда меньше знаменателя, так как N всегда больше ноля. Можно сказать, что коэффициент стандартизирован «не в полной мере». Второй, более существенный недостаток заключается в том, что он никак не учитывает степени свободы матрицы, число строк и столбцов. Соответственно, коэффициенты, полученные для матриц разного размера, несопоставимы.

В нашем примере.

т.е. фиксируется средняя по силе связь.

2. Критерий Фишера (ф или р):

Этот коэффициент — самый простой с вычислительной точки зрения, но он имеет очень сильное ограничение.

Критерий Фишера рассчитывается только для матриц размера 2×2, в противном случае его значение может превысить единицу.

3. Критерий Крамера (V):

где к — наименьшее из числа строк т и столбцов п.

Так, для нашего примера т = 2, п = 3, следовательно,.

к = т = 2. Расчет дает F = I——— = 0,48. Эта оценка.

V 1000(2−1).

несколько выше, чем оценка сопряженности Пирсона, но, в целом, близка к ней. Силу связи можно охарактеризовать как среднюю. Данный критерий представляет собой модификацию критерия Фишера, — в формуле частично учитываются степени свободы.

Все критерии, основанные на х², являются симметричными (ненаправленными); это означает, что критерий не «различает» зависимых и независимых переменных. Оценка связи для пары (х, у) будет такой же, как для пары (у, х).

Альтернативной критерию у} стратегией оценки силы связи между категориальными переменными является расчет критерия лямбда (X) и его модификаций. Она предполагает рассмотрение участвующих в анализе переменных как зависимой и независимой. Соответственно, здесь оценка силы связи для пары (х, у) будет отличаться от оценки для пары (у, х). Центральная идея критерия состоит в том, чтобы сравнить прогноз, сделанный на основе распределения зависимой переменной, с прогнозом, сделанным на основе совместного распределения зависимой и независимой переменных. Рассмотрим эту логику более детально на примере.

Допустим, нас интересует связь между членством в политической партии (М) и участием в выборах (V). Обе переменные — номинальные дихотомические. М принимает значения 1 — «является членом партии» и 2 — «не является членом партии»; V принимает значения 1 — «голосует на выборах», 2 — «не голосует». Матрицу сопряженностей см. в табл. 8.14.

Сначала будем исходить из того, что членство в партии является независимой переменной, а голосование на выборах — зависимой. Представьте, что перед вами 100 карточек, на каждой из которых снизу написано значение зависимой переменной: «голосует» (1) или «не голосует» (2). Но вы не видите, какие именно значения записаны на карточках; при этом требуется правильно угадать как можно больше значений.

В первом случае вы располагаете только обшей информацией о распределении переменной «участие в выборах». Голосует на выборах 55 респондентов (55%), не голосует — 45 (45%). Верной стратегией в такой ситуации будет следующая: надо все время называть значение с наибольшей частотой (модальное значение). Тогда вы будете правы в 55% и неправы в 45% случаев (см. рис. 8.16).

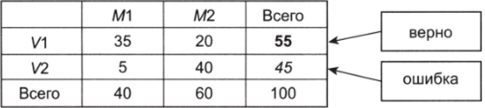
Рис. 8.16.

Теперь несколько изменим условия нашего эксперимента — воспользуемся информацией о независимой переменной «членство в партии». Пусть на каждой карточке сверху будет написано значение этой переменной: М или М2. Это дает нам возможность сделать предсказание относительно участия респондента в выборах, основываясь на его членстве в партии. Имеющаяся в нашем распоряжении матрица сопряженностей позволяет предположить, что большая электоральная активность характерна для тех, кто состоит в политической партии.

Стратегия угадывания меняется: теперь, если мы видим, что на карточке сверху написано Ml (член партии), мы называем значение И (участвует в выборах). Соответственно, значение М2 определяет наш выбор в пользу V2.

Здесь мы будем правы в 75% и неправы в 25% случаев (см. рис. 8.17).

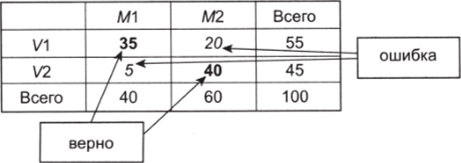
Рис. 8.17.

Основываясь на предположении о наличии связи между переменными, нам удалось существенно снизить долю ошибочных ответов: с 45 до 25%. Именно эти числа и являются основой для расчета критерия лямбда:

где ?, — вероятность ошибки на основе распределения зависимой переменной; Е₂ — вероятность ошибки на основе совместного распределения независимой и зависимой переменных.

Как и для других стандартных коэффициентов связи, близость к к 1 означает сильную связь, близость к 0 — слабую или отсутствующую.

В нашем примере А.(М, К) = ^' ^???^•— = 0.44. При этом последовательность переменных в скобках важна: это оценка силы связи в предположении, что независимой переменной является членство в партии. Предположим теперь, что независимая переменная — голосование на выборах. Такая гипотеза значительно менее логична, но с точки зрения математики столь же правомерна. Теперь вероятность ошибки с опорой только на распределение членства в партии составит 0,4; вероятность ошибки с опорой на участие в выборах — те же 0,25.

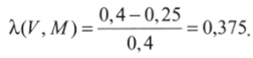
Обратите внимание, что Х (V, М) * ЦМ, V). Оценки связи, обладающие этим свойством, называют «направленными» (directional).

Основными модификациями критерия лямбда являются тау (т) Гудмана—Крускала и коэффициент неопределенности.

Основываясь на той же самой логике, что и «материнский» критерий, они характеризуются более сложным математическим аппаратом, который мы не будем здесь рассматривать. Все принципы интерпретации результата те же, что и для критерия лямбда.

Доннеми Р. Статистика. М., 2006. С. 267−282.

Иванов О. В. Статистика: Учебный курс для социологов и менеджеров. М" 2005. Ч. 2. С. 84−99.

Кремер Н.Ш. Теория вероятностей и математическая статистика. М" 2007. С. 395−398.

Мангейм Дж., Рич Р. Политология. Методы исследования. М., 1997. С. 408−426.

Петрунин Ю.Ю. Информационные технологии анализа данных. М" 2008. С. 139−146.

Интернет-ресурсы.

Clayton State University, School of business. Electronic Textbook on Business Statistics, http://business.clayton.edu/arjomand/book/sbk28.htm.

• [1] Использован рисунок http://www.nsu.ru/mmf/tvims/chernova/ms/lec/ node34.html.