Логический вывод в ИВ

Ранее мы говорили о выводе общезначимых формул (тавтологий, тождеств) из базовой системы аксиом. Рассмотрим вопрос вывода шире. Пусть имеется множество необщезначимых формул (Е_{), (Е₂), (?₃), (?"), обладающих тем свойством, что при некоторых интерпретациях они одновременно принимают значение И. Формула (В) выводима из множества {?}, если она может быть выведена из него путем применения правила заключения. (Правило подстановки применяется только для общезначимых формул.) Технически процесс вывода будет заключаться в получении ряда последовательных формул (Bj), (В₂), (В₃), …, каждая из которых выводится из всех (Е,) плюс те (В^), что уже получены прежде. Процесс длится до тех пор, пока одна из очередных (В_к) не совпадет с (В), т. е. когда B_k = В.

Правило заключения не меняет истинности и потому справедливо утверждение, что если (В) выводима из {?}, то она должна принимать значения И при тех же интерпретациях, что и все (В,). (Формулы (?,) могут принимать различные значения. Речь идет о значениях истинности, общих для их всех и (В) в том числе.).

Пишут:

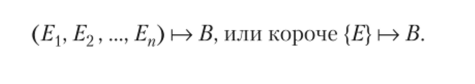
Говорят также, что (В) есть логическое следствие из посылок {?}. Вывод из системы аксиом теперь можно рассматривать как частный случай, когда выполняется условие ь-> {Л} I—> В.

Пример 3.5

Знакомое нам правило заключения можно переписать следующим образом: (/7, р —> I—> q, т. е. q — логическое следствие посылок р и р —> q. Справедливость этого легко проверяется, но таблице истинности: высказывание q принимает значение Я, как только р и (р —" q) одновременно принимают значение И.

Проблема вывода сводится, таким образом, к проблеме дедукции, которая формулируется следующим образом: требуется определить, является ли формула В логическим следствием множества формул {Е}.

Чтобы подчеркнуть, что E_t не являются аксиомами, их иногда обозначают через Hj и называют гипотезами, а формулу (В) — заключением:

Если гипотезы рассматривать как посылки в рассуждении, то из определения логического следствия вытекает, что заключение истинно только тогда, когда все посылки истинны. Заметим также, что если для множества {?} не существует такой интерпретации, при которой все (?,) принимают значения И, то множество {?} считается невыполнимым и обозначается:

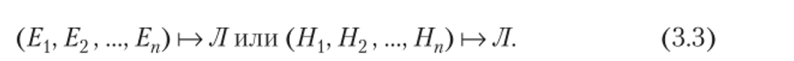
Сразу же отметим одно важное свойство, следующее из определения логического следствия. Если {?} В, то В принимает значение И, как только все Е_х также принимают значение истинности. Исключается, таким образом, случай, когда В = JI при всех E_i = И (обозначим: {?} = И). Остальные варианты вполне допустимы. Сведем их в табл. 3.3, добавив столбец с импликацией, которая нам сейчас пригодится.

Таблица 33

Варианты логических следствий

Из табл. 3.3 следует очевидный и важный вывод: если В — логическое следствие из множества {?}, то импликация {?} —> В тождественно истинна.

Условие одновременной истинности всех Е_х соответствует требованию конъюнкции. Следовательно, можно написать:

или иначе.

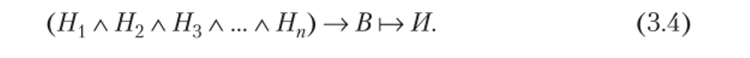
Известное нам правило заключения может быть записано следующим образом:

Пример 3.6.

Если q — логическое следствие из р и р —> q, то выражение должно быть тождеством.

Покажем эго. Приведем ППФ (Ь) к конъюнктивной нормальной форме (дизъюнкцию будем обозначать «+»).

Освободимся от импликаций и преобразуем:

К выражению © применим распределительный закон раскрытия конъюнкции по дизъюнкции:

Полученная конъюнктивная форма (d), очевидно, тождественна, поскольку каждый из двух ее дизъюнктов равен И (поскольку р + р = И_} q + q = И), что и требовалось доказать.

В данном примере мы вновь встретились с задачей определения тождественности формулы. В более общей формулировке она будет встречаться нам и в дальнейшем: требуется определить, к какому из трех классов принадлежит данная формула, — является ли она: а) тождественной; б) невыполнимой или в) выполнимой. В этом состоит проблема разрешения.