Инерционное преобразование детерминированного сигнала

Расчет реакции y (t) инерционного ИУ на заданный входной сигнал x (t) является основной задачей динамики ИУ. При решении этой задачи необходимо, зная характеристики входного сигнала x (t) и характеристики ИУ, определить характеристики выходного (преобразованного) сигнала y (t). Для линейных И У существуют строгие методы решения этой задачи. Для нелинейных ИУ точное решение возможно лишь для ограниченного числа случаев. В этом случае применяют приближенные и численные методы.

В табл. 8.1 показаны наиболее распространенные методы решения этой задачи для линейного ИУ: метод интегрирования дифференциального уравнения, метод интеграла наложения, спектральный метод, метод пространства состояний и операционный метод. Для каждого метода приведена основная расчетная формула. Рассмотрим эти методы.

Таблица 8.1

Методы решения основной задачи динамики ИУ.

Метод интегрирования дифференциального уравнения ИУ сводится к решению этого уравнения. Дифференциальное уравнение линейных стационарных ИУ имеет вид (5.1). Если известны параметры ИУ и входной сигнал x (t)_f то для определения функции y (t) нужно сначала определить общее решение соответствующего однородного (с нулевой правой частью) дифференциального уравнения y_CB(t), а затем найти частное решение уравнения (5.1) y_B(t), зависящее от вида правой части этого уравнения.

Сумма найденных решений образует семейство функций времени, содержащих п неизвестных величин, называемых произвольными постоянными. Их значения можно найти из условий, наложенных на значения выходного сигнала y (t) и всех его производных по времени до (гс-1)-го порядка включительно в какой-либо момент времени t = t₀ или какие-либо разные моменты времени. Если ?₀ = 0, то такие условия называются начальными условиями. Функция времени y (t) = y_CB(t) + y_B(t), удовлетворяющая этим условиям, описывает реакцию ИУ на заданный входной сигнал, т. е. является решением рассматриваемой задачи.

Метод интеграла наложения сводится к применению формул свертки (5.35), в частности формулы.

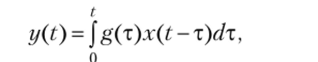
г&е g (T) = Lr* {W (р)} — весовая функция ИУ.

При решении задачи спектральным методом используют формулу.

где W (/'со) — комплексная частотная функция И У (5.56); G_x( со) — спектральная плотность входного сигнала, вычисляемая, но формуле (7.45).

При использовании метода пространства состояний дифференциальное уравнение ИУ (5.1) преобразуется в систему п дифференциальных уравнений первого порядка.

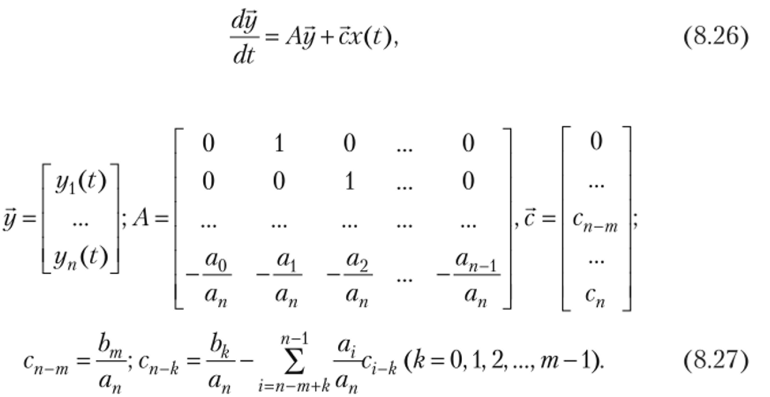
где В этом случае элементы y₂(t)_f…*y_n(t) вектора у образуют про

странство состояний и называются фазовыми координатами. Выходной сигнал И У y (t) совпадает с элементом y (t) этого вектора.

При использовании операционного метода считается, что входной сигнал x (t) имеет изображение (см. приложение 1).

прикладывается к входу ИУ, начиная с момента t = 0, и может иметь конечное число точек разрыва первого рода. На рис. 8.2 показан пример такого сигнала.

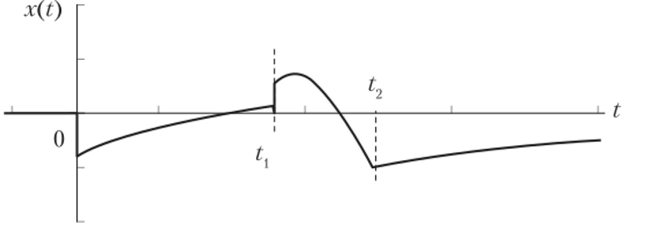
Рис. 8.2. Пример кусочно-непрерывного входного сигнала.

Условие x (t) = 0 при t<0 не сужает рассматриваемую задачу, так как предшествующее действие входного сигнала можно учесть в его начальных значениях лг (О-), х (О-),… х (^от₁)(0-). Если сигнал прикладывается ко входу И У в момент t = О, то все они равны нулю.

При решении задачи нужно также учитывать начальные условия, которые накладываются на выходной сигнал ИУ и значения всех его производных до (п — 1)-го порядка включительно.

Если они нулевые, то считается, что до момента? = 0 ИУ покоилось. Если, начиная с этого момента, во входном сигнале имеет место скачок (как это показано на рис. 8.2), импульс, или, как принято выше, именно в этот момент происходит «включение» входного сигнала, то нужно различать, что именно описывают (и предписывают) начальные условия: состояние ИУ в момент t = 0— (непосредственно перед скачком), или его состояние в момент t = 0+ (сразу же после скачка).

Если до момента t = 0 ИУ находилось в состоянии покоя, то в качестве начальных условий нужно принять равенства.

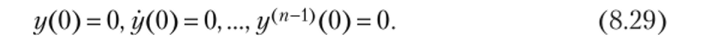
В противном случае в качестве начальных условий нужно считать, что.

Если т> 0, т. е. правая часть дифференциального уравнения ИУ (5.1) содержит операции дифференцирования входного сигнала, то значения функции y (t) и ее производных порядка выше (п-т-1) в точке f = 0 + могут не совпадать с их значениями в точке t = 0- [8J.

Решение задачи операционным методом выполняется в следующем порядке. Сначала, зная входной сигнал x (t), определяют его изображение Х (р) (8.28) (см. приложение 1). Затем, зная передаточную функцию ИУ W (p) и учитывая начальные условия, находят изображение выходного сигнала Y (p). Если начальные условия нулевые и сигнал x (t) прикладывается ко входу ИУ в момент t = 0, то это изображение вычисляется по формуле.

aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">

Если хотя бы одно из этих условий не выполняется, то вместо уравнения (8.31) нужно записать другое (расширенное) уравнение Дополнительное слагаемое F (p) вычисляется по формуле где.

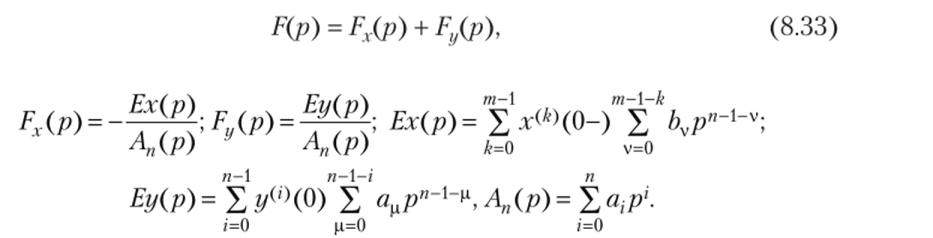
Слагаемое F_x(p) зависит от начальных значений входного сигнала .г^(0^-)> k = 0,1,2,т-1, а слагаемое F_y(p) — от начальных условий у (*>(0), i = 0, 1,2,…, п — 1. Если они нулевые, то F_x(p) = 0 и F_y(p) = 0, т. е. F (p) = 0.

В зависимости от порядка т полинома в числителе передаточной функции И У (5.7), формулы для слагаемого F_x(p) приводятся к виду:

• • если т = О, то F_x(p) = 0;
• 1
• • если т = 1, то F_x(p) =—{^(О-)};

АХр).

• если т = 2, то F_x(p) = —-j— {/>]Х (0-) + b₂[px (0-) + х (0-)]};

Р)

• если т = 3, то.

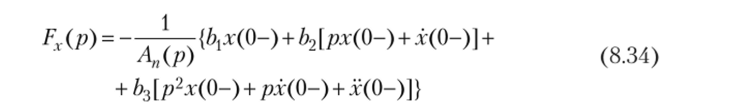
и т.д. Аналогично для слагаемого F"(p) можно записать:

• 1
• • если п = 1, то F_y(p) = —— {а, г/(0)};

^ЛпР)

• 1
• • если п = 2, то F_y(p) = ——{a_{y (0)+a₂[py (0) + y (0)]};

^ЛПР)

• если п- 3, то.

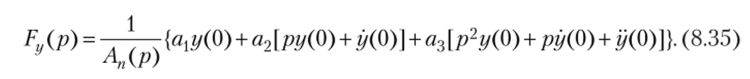
После этого решение задачи сводится к определению оригинала найденного изображения по формуле.

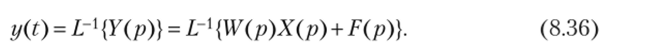
Описанная схема решения задачи показана на рис. 8.3.

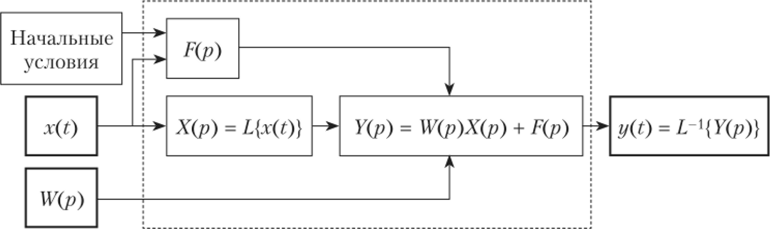
Рис. 83. Схема решения основной задачи динамики ИУ операционным методом.

В соответствии с этой схемой для решения задачи нужна передаточная функция ИУ W (p). Ее можно определить, зная любую полную динамическую характеристику ИУ (см. табл. 5.2).

Определение изображения Х (р) и оригинала y (t) можно выполнять с помощью таблиц преобразования Лапласа (см. приложение 1, табл. 1), что упрощает решение задачи.

Таким образом, в общем случае реакция линейного стационарного инерционного ИУ y (t) на входной сигнал x (t) содержит три слагаемых.

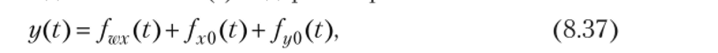
где — оригиналы соответствующих изображений.

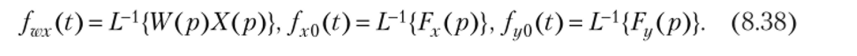
Слагаемое f_wx(t) называется вынужденной составляющей выходного сигнала, слагаемое /_v0(O — свободной х-составляющей, а слагаемое / ₀(t) — свободной «/-составляющей. Если сигнал x (t) прикладывается ко входу ИУ в момент t = 0 и начальные условия нулевые, то составляющие /хо (О ^и fyo (t) отсутствуют.

Покажем пример решения рассматриваемой задачи.

Пример 8.1.

Пусть на вход ИУ с передаточной функцией.

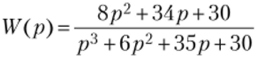
в момент? = 0 поступает сигнал x (t) = (t + l)³e" (*⁺¹). Требуется определить выходной сигнал ИУ, соответствующий заданным начальным условиям i/(0) = у₀, y (0) = v₀, y (0) = ze>₀.

Решение

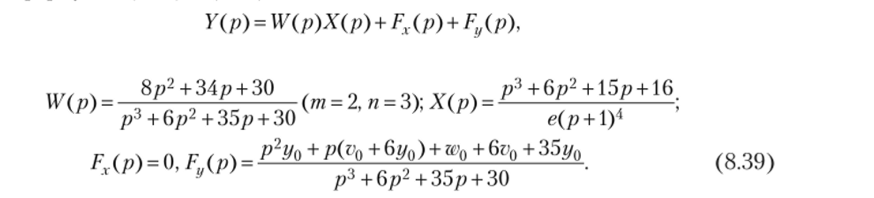
В частности, для случая у₀ = 1, v₀ = -2, w₀ = 2 получим По формулам (8.32) и (8.33) находим где.

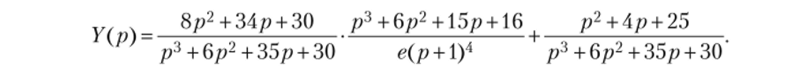
На рис. 8.4 построены графики входного сигнала x = x (t) (кривая 1) и соответствующего выходного сигнала y (t) = Lr^l{Y (p)} (кривая 2).

Рис. 8.4. К примеру решения основной задачи динамики ИУ операционным методом.

Используя теорему о предельных значениях (см. приложение 1, формулу (12)), можно найти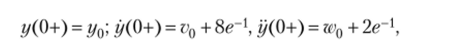

т.е. при t = О имеют место скачки скорости и ускорения. Это связано с наличием операций дифференцирования входного сигнала в правой части дифференциального уравнения рассматриваемого ИУ.

Штрихпунктирной кривой 3 показано решение, соответствующее нулевым начальным условиям г/₀ = 0, v₀ = 0, ге₀ = 0.

В работе [28] рассмотрены особенности расчета реакции линейного стационарного ИУ на непрерывный, импульсный, периодический и кусочнолинейный сигналы.