Лабораторный практикум. 
Основы проектирования приборов и систем

Лабораторный практикум дисциплины ОПИПС включает в себя занятие, посвященное освоению программы Mathcad (см. параграф П2) и три лабораторных занятия, посвященных изучению характеристик первичных измерительных преобразователей.

Лабораторная работа «Тензорезистивные датчики»

Цель работы — разработка математических моделей и сравнительный анализ мостовых тензорезистивных датчиков.

Объект исследований. Объектом исследований являются тензорезистивные датчики (ТНЗРД), содержащие один или нескольких тензорезисторов (ТНЗР), включенных в четырехплечий мост Уитстона (рис. П3.1).

Рассматриваются шесть вариантов схем включения тензорезисторов:

• 1) с одним ТНЗР и равноплечим мостом (РПМ1) (рис. П3.1, а);
• 2) с одним ТНЗР и последовательно-симметричным мостом (ПОСМ1) (рис. П3.1, б);
• 3) с одним ТНЗР и параллельно-симметричным мостом (I1PCM1) (рис. П3.1, в);
• 4) с двумя дифференциально включенными ТНЗР и последовательносимметричным мостом (IIOCM2) (рис. ИЗ. 1, г);
• 5) с двумя дифференциально включенными ТНЗР и параллельно-симметричным мостом (ПРСМ2) (рис. П3.1, д);
• 6) с четырьмя дифференциально включенными ТНЗР и равноплечим мостом (РПМ4) (рис. П3.1, е).

Схемы 1, 2, 3 с одним тензорезистором применяют редко из-за существенной нелинейности статической характеристики ТНЗРД и большой температурной погрешности. Эти недостатки проявляются в значительно меньшей степени при использовании схем 4, 5 с дифференциальным включением двух тензорезисторов, тем более — при использовании четырехплечей схемы 6. В ходе выполнения лабораторной работы эти различия приобретают числовую оценку.

Мост рис. ИЗ. 1 может питаться от источника постоянного напряжения U или от источника постоянного тока I. В первом случае информативным параметром выходного сигнала ТНЗРД считается напряжение U_x, во втором — ток 1_Х в измерительной диагонали моста ab.

Описание лабораторной установки. Схемы ТНЗРД собираются с помощью лабораторной установки, показанной на рис. П3.2.

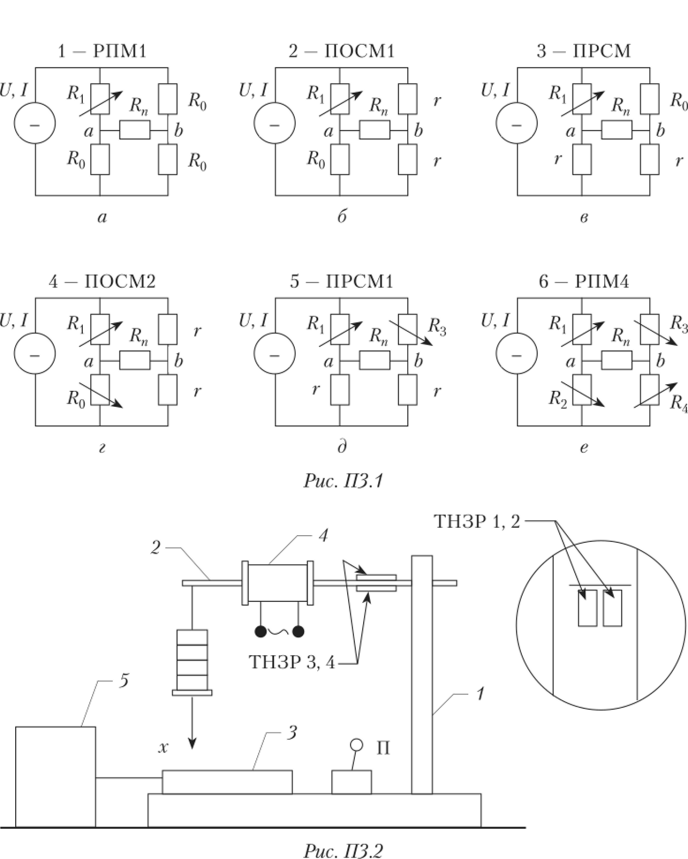
На штативе 1 закреплена балка 2 (упругая пластина). На верхней и нижней сторонах балки вблизи мест ее крепления наклеены по два тензорезистора — ТНЗР 1, 2 и ТНЗР 3, 4 соответственно Справа от рисунка показан вид балки сверху. Вид балки снизу аналогичен. С помощью переключателя П тензорезисторы могут включаться в схему моста 3 в соответствии с рис. ПЗ. 1. Измеряемое усилие х, создаваемое с помощью калиброванных грузов Г1, Г2, ГЗ, Г4 (масса каждого — по 100 г), прикладывается к свободному концу балки.

Для нагревания балки (и тензорезисторов) используется тепловыделяющий элемент — катушка 4, подключаемая к источнику переменного тока.

При нагружении балки ее верхние волокна растягиваются, а нижние — сжимаются. В результате сопротивления тензорезисторов ТНЗР 1, 2 увеличиваются, а тензорезисторов ТНЗР 3, 4 — уменьшаются. Это приводит к нарушению состояния равновесия моста и в его измерительной диагонали ab появляются напряжение U_x, или ток 1_Х> зависящие от измеряемого усилия х (веса груза). Их значения считывают, но шкале вторичного прибора 5.

Источниками погрешности измерений являются нелинейность статической характеристики датчика и изменение температуры окружающей среды.

Модель объекта исследований. Математической моделью датчика считается его расчетная статическая характеристика, т. е. уравнение, связывающее напряжение U_x (или ток 1_Х, в зависимости от варианта задания) с измеряемой величиной х и параметрами датчика. Это уравнение предлагается получить самостоятельно.

Если мост питается от источника постоянного напряжения U, то для этого можно использовать формулу.

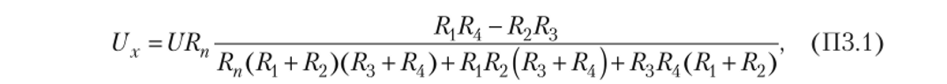
где R_Xy R₂, Я₃, R_a — сопротивления плеч моста; R_n — сопротивление нагрузки. Если мост питается от источника постоянного тока /, то.

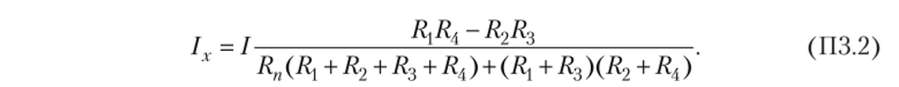
Для исключения размерности пользуются безразмерными статическими характеристиками датчика.

В обоих случаях зависимость сопротивлений тензорезисторов от измеряемой величины считается линейной, т. е.

где R₍₎ — сопротивление ненагруженного тензорезистора; а_д. — относительная чувствительность тензорезистора. Знак в формуле (П3.4) зависит от расположения тензорезисторов на балке: для верхних тензорезисторов используется знак «плюс», для нижних — «минус». Считается, что все тензорезисторы идентичны, т. е. имеют одинаковые значения параметров R₀ и а_г

В зависимости от вида схемы включения тензорезисторов в формулах (П3.1) и (П3.2) нужно принять (см. рис. 3.10, б):

• • для схемы 1 — R[ = /?₀(1 + a*#); R₂ = R₃ = R_A = R₀] (ПЗ.5.1)
• • для схемы 2 — R = /?₀(1 + oyt:); = /?₀; R₃ = R_A = r; (П3.5.2)
• • для схемы 3 — R = Rq (1 + R₃ = i?₀; R₂ = R_A = r (П3.5.3)
• • для схемы 4 — R- /?₀(1 + оуг); О «ol_xx); R₃ = R_A = г; (П3.5.4)
• • для схемы 5 — R = /?₀О + сх^дс); R₃ = R₀( 1 — a_xx); R₂ = R_A = r; (П3.5.5)
• • для схемы 6 — R_x = R_A = R₀( 1 + а_Лх); R₂ = R₃ = R₀ (1 — a_xx). (П3.5.6)

Подставляя эти выражения в формулы (П3.1) и (П3.2), можно получить расчетную статическую характеристику датчика, работающего в режиме заданного напряжения и, соответственно, заданного тока.

При изменении температуры балки Г значения параметров R₀ и а_х статической характеристики тензорезисторов (П3.4) изменяются, что приводит к появлению температурной погрешности датчика. В первом (линейном) приближении справедливы соотношения (см. 2.24).

где a_R, a_s — температурные коэффициенты величин /?₀, a_v; АТ = ТТ_п — отклонение температуры Т от нормальной температуры Т_п = 20 °C. Поэтому в возмущенном режиме измерений вместо формулы (П3.4) следует использовать выражение Подставляя это выражение в формулы (П3.6) и (П3.7), а затем — в формулы (П3.1) или (П3.2), можно найти абсолютную температурную погрешность исследуемого ТНЗРД.

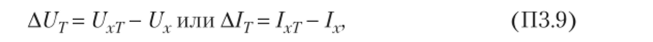
где U_xT, 1_хТ — выходные напряжение и ток, вычисленные с учетом фактического значения температуры Г; U_v 1_Х — то же для нормальной температуры Г_н = 20 °C.

Задание. В ходе выполнения работы осуществляются разработка математических моделей и сравнительный анализ двух различных схем включения тензорезисторов, показанных на рис. П3.1 и, соответственно, двух различных тензорезистивных датчиков. Отдельно рассматриваются невозмущенный (соответствующий нормальной температуре) и возмущенный (соответствующий фактической температуре) режимы измерений.

Критериями для сравнения являются относительная чувствительность и погрешность от нелинейности статических характеристик сравниваемых датчиков, а также максимальное значение и характер распределения температурной погрешности датчиков по диапазону измерений. Их находят на основе результатов анализа экспериментальных данных и (или) математических моделей сравниваемых датчиков.

Сочетание датчиков, подлежащих сравнению, задается преподавателем и указывается в индивидуальном варианте задания в виде шифра, цифры в котором обозначают номера схем включения сравниваемых датчиков, а буквы — тип источника питания. Например, шифр 45U означает, что сравниваются датчики, имеющие схемы 4 и 5, работающие в режиме заданного напряжения. Шифр 45 Т означает, что эти датчики питаются от источника постоянного тока. Шифр 1U5T означает, что сравнению подлежат характеристики датчика с одним тензорезистором, включенным в равноплечий мост, работающий в режиме заданного напряжения (схема 1), и датчика с двумя тензорезисторами, дифференциально включенными в параллельносимметричный мост (схема 5), работающий в режиме заданного тока.

Модель ТНЗРД может строиться на основе сведений о номинальных значениях параметров сравниваемых датчиков или на основе экспериментальных данных.

В качестве номинальных принимаются следующие значения параметров:

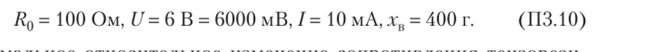
Максимальние относительное изменение сопротивления тензорезисторов, обусловленное воздействием измеряемой величины, принимается равным 1%, т. е. считается, что а_гг_в = 0,01. Максимальные температурные изменения начального сопротивления и чувствительности тензорезисторов принимаются равными 0.1%. т. е.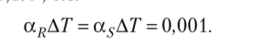

Сопротивления г и R_n определяются в соответствии с данными табл. 2.6, т. е. принимается:

• для последовательно-симметричной и равноплечей схем моста (схем 1, 2, 4, 6 на рис. 113.1)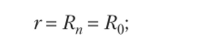

• для параллельно-симметричных мостов, работающих в режиме заданного напряжения (схем 3, 5, U)

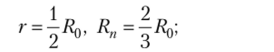
• для параллельно-симметричных мостов, работающих в режиме заданного тока (схем 3, 5, 7)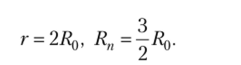

В этих случаях чувствительность ТНЗРД максимальна.

Задачи исследований:

• 1) определение расчетных статических характеристик сравниваемых ТНЗРД;
• 2) определение градуировочных статических характеристик сравниваемых ТНЗРД;
• 3) определение средней чувствительности и погрешности от нелинейности статических характеристик сравниваемых ТНЗРД;
• 4) определение и анализ температурной погрешности сравниваемых ТНЗРД;
• 5) выводы по работе.

Рекомендации:

1) расчетная статическая характеристика мостовых ТНЗРД описывается одной из четырех формул (см. (2.21))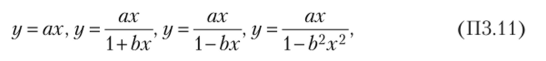

где у — информативный параметр выходного сигнала датчика (ток 1_Х или напряжение U_x в измерительной диагонали моста); а, b — постоянные коэффициенты, зависящие от параметров датчика.

На рис. 2.11, а показаны графики этих функций, в табл. 2.3 — формулы для расчета погрешности от их нелинейности, в табл. 2.5 — расчетные статические характеристики ТНЗРД, работающих в режиме заданного напряжсния, в табл. 2.7 — оптимальные значения параметров а, b расчетных статических характеристик ТНЗРД;

2) для определения статической характеристики конкретного варианта ТНЗРД удобно использовать программу Mathcad. В качестве примера покажем это для ТНЗРД типа 1U. В этом случае, используя формулы (П3.1), (ПЗ.5.1) и команду substitute (подставить), получим.

т.е. расчетная статическая датчика 1U имеет вид.

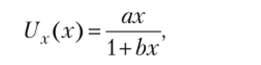
Ua с 3 + 2а R_n ,.

где а =——, о =-а_г, а = —^и~, что совпадает с формулами п. 1 табл. 2.5.

4(1 + а) 4(1 + a).

Для номинальных значений параметров датчика Ш имеем, а = 1, а^г_в =.

= 1%, ах. =———а_хх_п =7,5 мВ, q = bx = ^ ⁺ а г = 6,25 • 10^_3; ^в 4(1 +а) ^{д в 4} 4(1+а) * ^в

• 3) при определении градуировочной характеристики датчика рекомендуется использовать его расчетную статическую характеристику (П3.11). Расчет параметров а, b этой характеристики выполняется (по заданию преподавателя) методом наименьших модулей или методом наименьших квадратов;
• 4) при расчете погрешности от нелинейности статической характеристики датчика рекомендуется использовать формулы табл. 2.3 и 2.7. Например, для датчика 1U имеем:
  • • максимальная приведенная погрешность от нелинейности статической характеристики

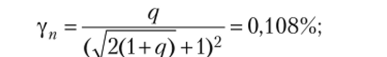
• средняя чувствительность датчика (коэффициент наклона ПНМ у_а = fir) равна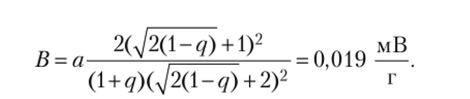

Расчет этих характеристик датчика можно выполнить в среде Mathcad;

5) при определении температурной погрешности датчика рекомендуется использовать формулы (2.27)—(2.32). В частности, из формулы (2.28) следует, что абсолютная температурная погрешность датчика 1U является аддитивной. Максимальное значение этой погрешности равно.

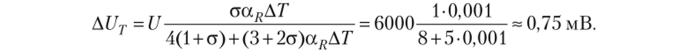
В соответствии с формулой (2.32) максимальная приведенная температурная погрешность такого датчика равна.

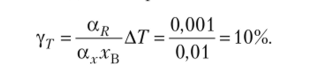
Для определения температурной погрешности датчика удобно использовать программу Mathcad. Для этого нужно подобно вычислениям (113.12) определить номинальную статическую характеристику датчика для нормального и возмущенного режимов измерений, а затем — соответствующую абсолютную температурную погрешность (П3.9). Например, для датчика Ш имеем:

• при нормальном режиме измерений:

На рис. 3.3, а показаны графики этих функций. Видно, что температурная погрешность датчика 1U аддитивная. Из рис. 3.3, 6 видно, что максимальная температурная погрешность такого датчика равна 0,755 мВ, соответствующая максимальная приведенная температурная погрешность равна 10%, что совпадает с прежними результатами;

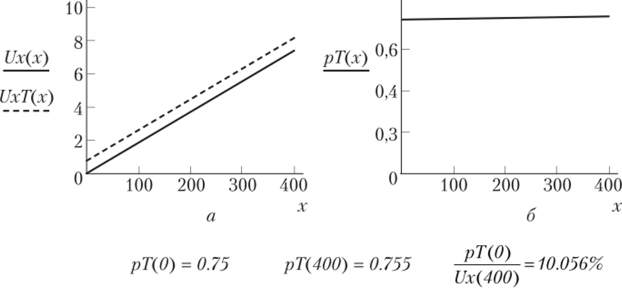
рТ (0) = 0.75 _РТ (400) = 0.755.

Рис. ПЗ.З

6) в выводах по работе необходимо, используя полученные результаты, дать заключение о преимуществах и недостатках сравниваемых датчиков.