Фрактальная геометрия природы

В XX в. был разработан теоретический язык, адекватно описывающий иерархические природные структуры, которые возникают в ходе эволюционного развития. Основное понятие этого языка — понятие фрактала. Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому (Б. Мандельброт; цит. по: Федер Е. Фракталы. М.: Мир, 1991. С. 19).

Фракталы — детища «сухой» математики, но они настолько эстетичны, что выставка фракталов, построенных с помощью компьютера, потрясла мир, а книга организаторов выставки, математиков X. О. Пайтгена и П. Рихтера, «Красота фракталов» раскупается как художественный альбом.

Они упорядоченны, но это не упорядоченность монотонного орнамента, повторяющего без изменений один и тот же мотив.

Они геометричны, но это не геометрия идеалиста Платона, искавшего везде отполированные формы правильных многогранников, а геометрия реального мира — ветвистого, пористого, шершавого, зазубренного, изъеденного. Не зря человек, давший фракталам имя, математик Бенуа Мандельброт назвал свой главный труд «Фрактальная геометрия природы» (1982).

Облака — не сферы, горы — не конусы, линии берегов — не окружности, и негладка древесная кора, и непрям путь молнии (Б. Манлельброт).

Козьма Прутков писал: «Многие веши нам непонятны не потому, что наши понятия слабы, а потому, что сии вещи не входят в круг наших понятий». Как только Мандельброт открыл понятие фрактала, оказалось, что мы буквально окружены ими. Фрактальны слитки металла и горные породы; фрактальны расположение ветвей, узоры листьев, капиллярная система растений; кровеносная, нервная, лимфатическая системы в организмах животных; фрактальны речные бассейны, поверхность облаков, линии морских побережий, горный рельеф…

? Основное свойство фракталов — самоподобие.

Любой микроскопический фрагмент фрактала в том или ином отношении воспроизводит его глобальную структуру. В простейшем случае часть фрактала представляет собой просто уменьшенный целый фрактал.

Отсюда основной рецепт построения фракталов: возьми простой мотив и повторяй его, постоянно уменьшая размеры. В конце концов получится структура, воспроизводящая этот мотив во всех масштабах, — бесконечная лестница вглубь.

Берем отрезок и среднюю его треть переламываем под углом 60°. Затем повторяем эту операцию с каждой из частей получившейся ломаной — и так до бесконечности. В конечном счете мы получим простейший фрактал — тприадпую кривую, которую в 1904 г. открыла математик Хельга фон Кох (рис. 4.13).

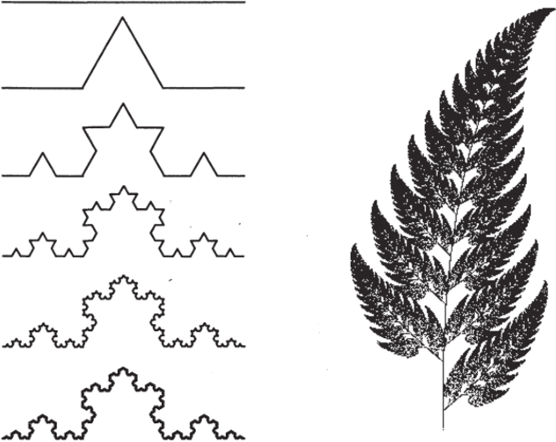
Рис. 4.13. Кривая Кох Рис. 4.14. Это не фотография.

папоротника, а фрактал Если проявить чуть больше изобретательности и на каждом шап не только уменьшать основной мотив, но также смещать и повора чивать его, можно получить более интересные и реалистически вы глядящие образования, например лист папоротника или даже папо родниковые заросли. А можно построить весьма правдоподобны? фрактальный рельеф местности и покрыть ее очень симпатичным ле сом. Большинство текстур местности в современных компыотерны? играх представляют собой фракталы.

Идея бесконечного повторения простой операции используете? для порождения еще более изощренных и удивительных структур (рис. 4.14).

Возьмем какое-нибудь число х₀ от 0 до 1 и рассчитаем.

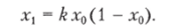
Затем точно так же по х, вычислим х₂, по х₂ — дг₃ и так далее. Еслг коэффициент к меньше 3, то последовательность чисел х, быстрс стремится к постоянному значению, в чем несложно убедиться. Если же взять к > 3, последовательность начинает метаться между двумя значениями, затем — четырьмя, восемью и т. д., пока наконец при к > 3,6 ее поведение внешне не станет совершенно беспорядочным. Но «если это и безумие, то в нем есть система», что хорошо видно на рис. 4.15, показывающем, какие значения могут принимать числа х_{ в зависимости от k. Структура, проявляющаяся на рисунке, — тоже фрактал, но фрактал сложный: подобие его частей целому не сводится к простому изменению масштаба.

Рис. 4.15. Поведение последовательности, генерируемой отображением x_i+1 — к x_k{ 1 — х,), при разных к.

Самые знаменитые фракталы — множества Жюлиа и Мандельброта — выращиваются повторением простой формулы z_n= z"² + с, где числа z_n и константа с считаются комплексными, т. е. изображаются точками не на числовой прямой, а на плоскости. Если ваша математическая подготовка не включает знакомства с комплексными числами, вы можете возложить расчеты на компьютерную программу Fractal Explorer; а сами любоваться готовыми результатами.

Безмерно множество Мандельброта, и никто не сможет пройти все закоулочки и извивы его берегов. Причину тому можно понять, еще раз взглянув на кривую Кох: на каждом шаге изготовления длина ее увеличивается в 4/3 раза. Путешественник по этой кривой обнаружит, что между ее началом и концом укладывается бесконечное число звеньев, общая длина которых также бесконечна. «Берег» множества Мандельброта также имеет бесконечно сложную структуру, которая не сглаживается ни при каком самом сильном увеличении.

Рис. 4.16. Множество Мандельброта. Серые точки соответствуют таким значениям с, что последовательность чисел z_n, стартуя с z₀ = 0, убегает на бесконечность.

Рис. 4.17. Берега множества Мандельброта.

Самое удивительное, что таким же свойством обладают реальные берега земных морей. Еще в 1901 г. английский географ Ричардсон обратил внимание, что длина береговой линии существенно зависит от масштаба карты, по которой измеряется. Чем крупномасштабнее карта, которой вы пользуетесь, тем более извилистым предстает берег, и с ростом подробности карты суммарный периметр всех его заливчиков и мысков растет бесконечно.

Все нормальные (т. е. гладкие) линии, имеющие начало и конец, имеют и конечную длину. Если же длина кривой, соединяющей две точки, бесконечна, то эта кривая уже не совсем линия. Геометрия фракталов подтверждает: да, и кривая Кох, и берег множества Мандельброта, и побережья островов и континентов являются чем-то промежуточным между линией и лентой. За счет своей бесконечной извилистости они как бы приобретают дополнительное измерение. И природа не упускает шанса воспользоваться лишними измерениями.

Например, давно известно, что частота дыхания у животных обратно пропорциональна корню четвертой степени из веса. Это обстоятельство ставило ученых в тупик: если считать, что объем кровеносной системы пропорционален весу, т. е. третьей степени размеров тела, то и частота дыхания должна изменяться как корень третьей степени из веса! Откуда же природа берет четверку?

Группа исследователей из университета Нью-Мексико предложила объяснение, основанное на идее о том, что эффективно устроенная кровеносная система должна максимально заполнять объем тела (рис. 4.18). А для этого она должна быть устроена фрактально, и объем такого фрактала оказывается пропорционален четвертой степени размеров. Четвертой, а не третьей! В своей статье в журнале Science авторы открытия пишут: «Хотя живые существа обитают в трехмерном пространстве, их внутренняя физиология и анатомия устроены так, как если бы они были четырехмерными… Фрактальная геометрия буквально придает жизни дополнительное измерение».

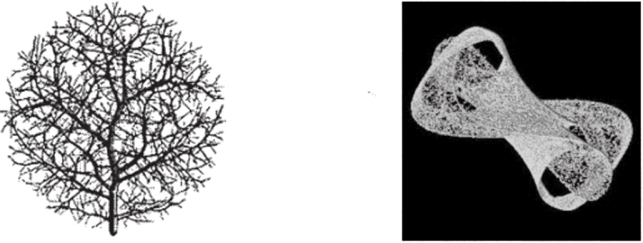
Рис. 4.18. Фрактальная геометрия кровеносной системы.

Рис. 4.19. Фрактальные траектории системы с динамическим хаосом

Фракталы очень тесно связаны с динамическим хаосом (п. 3.4.3). Если динамическая система (например, метеорит в окрестностях двойной звезды или фондовый рынок) начинает вести себя хаотически, то ее траектории превращаются во фракталы: они имеют тонкую структуру в сколь угодно малом масштабе. Подобно береговой линии или кровеносной системе эти фракталы нерегулярны, не подчинены требованию точного самоподобия. Тем не менее один взгляд на них убеждает в их упорядоченности. Такое поведение хаотично, но «хаос» в данном случае означает не отсутствие порядка, а очень сложный и нетривиальный порядок, обладающий чрезвычайно тонкой структурой. Естественно ожидать, что в результате длительного эволюционного процесса должны возникать именно такие сложные формы поведения природных систем (рис. 4.19).

Иерархия структурных уровней материи (по Н. Ф. Реймерсу, с сокращениями).