Уравнение линейной регрессии
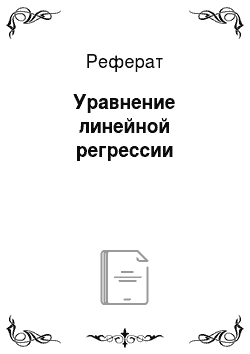
Где Yx — имеет смысл оценки условного математического ожидания M (Y/X=x); р) Х — сглаживающий выборочный коэффициент линейной регрессии У на X (эмпирическая оценка генерального коэффициента А); b — действительное число (оценка параметра В). Необходимым условием экстремума функции нескольких переменных является равенство нулю частных производных по параметрам. Приравнивая к нулю частные производные… Читать ещё >
Уравнение линейной регрессии (реферат, курсовая, диплом, контрольная)
Пусть имеется выборка значений пары случайных величин X и Y, которая представлена в виде набора (xiyi), (хг, уг),—-, (х,"у") или в виде табл. 8.2. На основе данных по выборке следует проверить гипотезу о наличии линейной корреляционной зависимости величины Y от величины X, т. е. когда есть основания предполагать, что генеральное уравнение регрессии имеет вид (8.2).
На практике оценкой генерального (истинного) уравнения линейной регрессии (8.2) является выборочное (эмпирическое) сглаживающее уравнение линейной прямой  регрессии Y наХ:
регрессии Y наХ:
где Yx — имеет смысл оценки условного математического ожидания M (Y/X=x); р)Х — сглаживающий выборочный коэффициент линейной регрессии У на X (эмпирическая оценка генерального коэффициента А); b — действительное число (оценка параметра В).
Для оценки параметров сглаживающего выборочного уравнения линейной регрессии Y на X по результатам выборочных наблюдений наиболее употребительным и точным методом является метод наименьших квадратов.
В методе наименьших квадратов требуется, чтобы сумма квадратов разностей S (p)x, b) наблюдаемых значений ух от значений Yx (х,) на линии прямой регрессии оказалась наименьшей:

Необходимым условием экстремума функции нескольких переменных является равенство нулю частных производных по параметрам. Приравнивая к нулю частные производные по параметрам р,<�х и Ь, получим следующую систему уравнений: 
Решая эту систему уравнений получим искомые параметры рух и b уравнения (8.5), если исходные данные представлены в виде двумерной выборки.

а если исходные данные представлены в виде корреляционной таблицы, то.

которые необходимо дополнить выборочной дисперсией случайной величины X

Аналогично вышеизложенному определяется выборочное (эмпирическое) сглаживающее уравнение линейной обратной регрессии Хна У 
Если исходные данные представлены в виде двумерной выборки, то входящие в правую часть уравнения (8.11) pw d и У2 находят по формулам.

а если исходные данные представлены в виде корреляционной таблицы, то.

которые необходимо дополнить выборочной дисперсией случайной величины У

При этом значения величин Х, Х2, У, ХУ в системе уравнений (8.12) находят по формулам (8.8).
Здесь уместно отметить, что выборочные средние квадратичные отклонения ох, оу случайных величин X, У равны квадратному корню из выборочной дисперсии и вычисляются соответственно по формулам:
Выборочный слаживающий коэффициент линейной регрессии рух показывает, на сколько единиц в среднем изменится переменная У, при увеличении переменной х на одну единицу, а знак при руг указывает направление корреляционной связи между признаками X к Y: при <0 — связь обратная, при рух >0-

связь прямая. Геометрически ру1 является угловым коэффициентом наклона прямой линии Yx.
Подчеркнем, что регрессия У на X не идентична регрессии X на У, т. е. У, и Xv — различные прямые (рис. 8.3, о), которые пересекаются в точке C (X, Y). Первая прямая получается в результате решения задачи о минимизации суммы квадратов отклонений по вертикали (рис. 8.3, б), а вторая — по горизонтали (рис. 8.3, в). Поэтому из уравнения Ух=рукх+Ь нельзя выразить х через Yx.
Например, если хотим оценить рост человека по массе, а также решить обратную задачу — сделать вывод о массе человека по росту, то нельзя пользоваться одним и тем же уравнением.

Рис. 8.3. Различные виды линий регрессии.
Отметим, что по своей форме и существу уравнение (8.5) точно такое же, как и линейная зависимость у=рх+Ь. Разница лишь в том, что у = рх + Ь дает функциональную зависимость величины у от х, а выражение (8.5) — корреляционную зависимость между случайными величинами У и X.
Пример 8.4. Используя условия примера 8.3, составить выборочное уравнение линейной прямой регрессии роста У на объем X грудной клетки мужчин.
Решение. По формулам (8.8) вычислим средние арифметические и остальные значения случайных величин X и У, а по формуле (8.10) выборочную дисперсию:

Используя найденные значения, по формулам (8.7) вычислим параметры.

и в соответствии с формулой (8.5) получим искомое выборочное уравнение линейной прямой регрессии роста на объем грудной клетки мужчин 
Пример 8.5. Составить выборочное уравнение линейной прямой регрессии У на X и выборочное уравнение линейной обратной регрессии X на У на основании данных табл.8.14.
Таблица 8.14. Корреляционная таблица.
'Ч х у ч. | ту | ||||||
1Пх | ЮЗ. |
Решение. По формулам (8.9) находим средние арифметические значения величин X и У:

Определим остальные значения этих величин  а также выборочную дисперсию
а также выборочную дисперсию  .
.
Подставляя полученные данные в (8.7), найдем параметры ру, и Ь:

и в соответствии с (8.5) выборочное уравнение линейной прямой регрессии У на X  .
.
Для получения уравнения регрессии Хна У вычислим:

Далее по формулам (8.12) определим параметры уравнения линейной регрессии:

и в соответствии с (8.11) выборочное уравнение линейной обратной регрессии X на У принимает вид.

Пример 8.6. По данным, приведенным в примере 8.2, составить выборочное уравнение линейной прямой регрессии длины Y на диаметр X сегмента лимфатических капилляров эпикарда собаки, а также выборочное уравнение линейной обратной регрессии X на Y.
Решение. Пользуясь данными, приведенными в корреляционной табл. 8.9, по формулам (8.9) найдем средние арифметические значения диаметра и длины сегментов.

и остальные величины, необходимые для расчета параметров Рух и Ь выборочного уравнения линейной прямой регрессии.

которые дополним выборочной дисперсией.


Для исходных значений X, взятых из табл. 8.10, вычислим ординаты Г,1|иет выборочного уравнения линейной прямой регресИспользуя найденные величины, по формулам (8.7) вычислим параметры.

и в соответствии с формулой (8.5) получим выборочное уравнение линейной прямой регрессии длины на диаметр сегмента лимфатических капилляоов эпикаода собаки сии длины на диаметр сегмента и занесем их в третью строку табл. 8.15. Как следует из таблицы, расхождение исходных Ух
и расчетных значений ?х ^ невелико, т. е. искомое выборочное уравнение линейной прямой регрессии (8.17) достаточно качественное.
Таблица 8.15. Результаты расчета ординаты линейной регрессии.
X | |||||
у; | |||||
у ^х.расч. | 50,8. | 59,1. | 67,4. | 75,7. | 84,0. |
I уУ I 1-1д, расч лх | 1.8. | 0,9. | 2,6. | 0,7. | 1,0. |
Построим сглаживающую линию регрессии Т1расч (рис. 8.2, б).
Наглядно убеждаемся, что сглаживающая линия регрессии (сплошная кривая) является хорошим приближением ломаной линии регрессии Ух (штриховая линия).
Для получения выборочного уравнения линейной обратной регрессии X на У по формулам (8.14) и (8.15) вычислим:

Далее по формулам (8.12) определим параметры.