Коэффициент согласия в динамике

Ранее говорилось, что выводы математической статистики — типичные выводы, но индукции. Структурно различают четыре вида научной индукции, в логике традиционно называемых методами^[1].

• 1. Метод единственного сходства.
• 2. Метод единственного различия.
• 3. Метод сопутствующих изменений.
• 4. Метод остатков.

Тщательное изучение каждого из этих методов дается в учебниках по логике, поэтому здесь мы не будем останавливаться на особенностях каждого из них. Из этих методов нас интересуют два — метод единственного сходства и метод единственного различия, поскольку первый из них является методологической основой корреляционного анализа, а второй — дает базу для вычисления коэффициента согласия в динамике^[2]. Знакомство с указанными методами даст возможность понять различие между подходами к выявлению корреляции и суть каждого из них.

Метод единственного сходства — это умозаключение о причине наблюдаемого явления, основанное на сравнении нескольких случаев, влекущих за собой это явление.

Если два или более случая исследуемого (наблюдаемого) явления связаны только с одним (из нескольких) общим, предшествующим явлению обстоятельством, то оно и есть причина или часть причины исследуемого (наблюдаемого) явления.

Схематически структура данного метода может быть выражена следующим образом:

случай 1: BjBrj — обстоятельства, предшествующие явлению «а»;

случай 2: Б₂Г₂В — обстоятельства, предшествующие явлению «а»;

случай 3: ВБ3Г3 — обстоятельства, предшествующие явлению «а»;

случай 4: Б^В — обстоятельства, предшествующие явлению «а».

«В» является причиной или частью причины явления «а».

Именно этот вид индуктивного вывода и лежит в основе вычисления коэффициента парной корреляции. Действительно, логику этой части корреляционного анализа можно сформулировать так: имеется ряд значений у₍ и ряд значений x_v которые можно рассматривать, в соответствии со схематической структурой метода единственного сходства как обстоятельства Б_1? Б₂, Б₃ Г_1? Г₂, Г₃… Между ними имеется линейная зависимость (обстоятельство «В»). Для таких обстоятельств коэффициент корреляции близок к единице (явление «а»). Тогда и следует вывод: линейная зависимость («В») и является причиной высокого значения коэффициента парной корреляции («а»).

Как было показано в предыдущем параграфе, если все точки двух переменных, расположенных на одной плоскости, выстраиваются в фигуру, напоминающую прямую линию, коэффициент парной корреляции между ними всегда будет близок к единице (структура метода единственного сходства дает в данном случае правильный вывод). Другое дело, что например, возможно появление третьего фактора z_t, который и является истиной причиной высокого значения коэффициента парной корреляции, а он в этой схеме не рассматривается. Но на то он и индуктивный вывод, что дает вывод не однозначно истинный, а возможный.

Такой же вывод можно получить с помощью метода единственного различия, который представляет собой умозаключение о причине наблюдаемого явления, основанное на сравнении всего лишь двух случаев: когда интересующее нас явление имеет место и когда его нет. Если случай, в котором явление присутствует, отличается от случая, в котором его нет, только одним предшествующим явлению обстоятельством, то именно это обстоятельство и является причиной или частью причины данного явления:

случай 1: ВСД — обстоятельства, повлекшие явление «а»;

случай 2: СД — обстоятельства, не повлекшие явление, т. е. «—»;

«В» — причина или часть причины явления «а».

Корреляционный анализ базируется на априорном предположении о том, что изменения случайных факторов могут быть какими угодно, но они линейны относительно друг друга. Если же эти изменения относительно друг друга носят более сложный нелинейный характер, корреляционный анализ оказывается бессильным для выявления этой сложной взаимосвязи.

Взаимосвязь факторов, как известно, проявляется не только в наличии некоторой тенденции взаимного изменения, которую корреляционный анализ и пытается оценить, но и в характере отклонений от тенденций во времени каждого из них. Если, например, между двумя факторами имеется некоторая корреляционная взаимосвязь (не обязательно линейная), то это означает, что резкое изменение одного фактора вызовет аналогичное изменение другого фактора.

Зная это, можно предложить подход, базирующийся на методе единственного различия. Имеется ряд значений у_{ и ряд значений x_t, которые можно рассматривать, в соответствии со схематической структурой метода единственного различия как обстоятельства С и Д. Корреляционная взаимосвязь между факторами (обстоятельство «В») приводит к тому, что при изменении в тенденциях одного фактора наблюдаются изменения в тенденциях другого фактора (явление «а»). Когда между факторами нет взаимосвязи (обстоятельство «В» отсутствует), то динамика факторов «рассогласованна», т. е. резкий рост одного фактора никак не влияет на динамику другого (отсутствует явление «а»).

Следовательно, если удастся найти коэффициент, который будет характеризовать степень согласованности динамики показателей, по его значению можно будет судить о наличии или отсутствии взаимосвязи между факторами. Очевидно, что и в этом случае будет иметь место вывод по индукции, носящий предположительный, а не истинный характер.

Покажем, как можно получить коэффициент, обладающий подобными свойствами.

Известно, что по всем Т наблюдениям о показателе y_t (t = 1, 2, 3,…, 7), имеющимся в распоряжении исследователя, можно построить степенную функцию (Г — 1)-й степени:

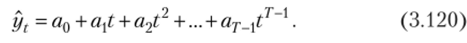
Причем этот полином так опишет исходный ряд наблюдений y_t, что его расчетные значения y_t в каждой t-й точке в точности будут соответствовать фактическим значениям y_t

Коэффициенты полинома (3.120) определяют динамические свойства анализируемого ряда. Поэтому по их значениям можно судить об исходном ряде и его свойствах. Очевидно, что каждый ряд, отличающийся в своей динамике от другого ряда, будет отличаться от него и своими коэффициентами, если оба ряда представить в виде модели (3.120). А если ряды в динамике меняются в среднем одинаково, то и коэффициенты степенной функции, в которую можно разложить любой ряд, будут во многом совпадать. Поэтому сравнительный анализ коэффициентов при одинаковых степенях может позволить получить искомую информацию о взаимосвязи факторов.

Но для того, чтобы осуществить такой сравнительный анализ, необходимо вычислить коэффициенты модели разложения функции в степенной ряд (3.120). Для этого есть несколько возможных вариантов:

• 1) построить степенные функции (Т — 1)-й степени
• (3.120), решая системы из Т уравнений с Т неизвестными коэффициентами а;
• 2) воспользоваться разложением функций в степенные ряды (ряды Тейлора) и анализировать соответствующие члены степенного ряда;
• 3) оценить параметры степенных функций с помощью аппарата конечных разностей;
• 4) найти различные производные степенной функции
• (3.120) с помощью метода конечных разностей, поскольку они вполне характеризуют соответствующие коэффициенты.

Первый вариант предполагает решение системы Т уравнений с Т неизвестными, что в ряде случаев при большом числе наблюдений Т представляет собой непростую вычислительную задачу, которую неразумно рекомендовать к широкому практическому использованию. К тому же полиномы высоких степеней очень неустойчивы к ошибкам округлений.

Второй вариант предполагает представление в явном виде самой функции, разложение которой необходимо осуществить, а она не известна. Существует большое количество различных методов, позволяющих найти приближенные коэффициенты рядов Тейлора. Однако их множество вызвано именно различной степенью неточности такого приближения и с удовлетворительной точностью этот вариант решен быть не может.

Третий вариант — оценить параметры степенных функций с помощью аппарата конечных разностей — значительно проще, чем все рассмотренные выше варианты, однако и он достаточно громоздок. Рассмотрим его более подробно, так как на основе этого рассмотрения можно будет увидеть особенности простого использования четвертого варианта.

Пусть нам дана линейная однофакторная модель

параметры которой а₀ и а_{ следует найти на множестве наблюдений Т.

Метод конечных разностей исходит из того факта, что первая производная линейной функции (3.122) будет равна яj, а одной из оценок этой производной может быть средняя первая разность.

Обозначим через Д^{у_г первую разность ряда в точке t. Эта разность вычисляется элементарно:

Она характеризует первую производную функции в точке t. Общей характеристикой первой производной на всем множестве значений может служить средняя этих разностей. Но поскольку первых разностей на единицу меньше, чем количество исходных членов ряда, то эта средняя будет вычисляться со второго члена ряда до последнего Т-го:

Подставляя в (3.124) значения разностей, полученные с помощью (3.123), и осуществив элементарные сокращения, получим окончательно:

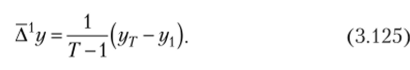
Эта средняя разность характеризует первую производную функции и дает некоторую оценку коэффициента а_х линейной функции:

Для нахождения параметра а₀ модели (3.122) по известному значению коэффициента а_{ необходимо найти средние значения у и t, подставить их в (3.122) и, решив уравнение, определить значение а₀.

Такую же процедуру можно провести с рядом значений другого показателя, который обозначим через х_?: x_t =b₀ + b_{t.

После этого можно сравнить друг с другом коэффициенты а₀ и /;₀, а_х и Очевидно, что они должны быть либо безразмерными, либо одной размерности.

Если теперь предположить наличие тенденции роста, описываемой с помощью параболы второй степени.

то для определения параметра а₂ этой модели необходимо рассчитать вторые разности:

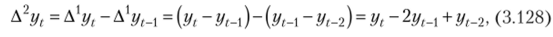
а затем найти среднюю вторых разностей. Поскольку вторых разностей на единицу меньше, чем первых, средняя вторых разностей вычисляется так:

Известно, что вторая разность характеризует вторую производную любой функции, а применительно к функции (3.127) она будет характеризовать значение коэффициента а₂, поскольку вторая производная указанной функции равна 2а₂.

Подставляя в (3.129) значения вторых разностей из (3.128), которые, в свою очередь, определяются через первые разности (3.123), после ряда элементарных сокращений получим.

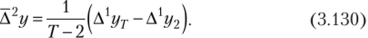
Отсюда легко найти оценку коэффициента а₂:

Теперь для нахождения неизвестных значений коэффициентов я₀ и я, следует воспользоваться процедурой, описанной для линейной модели, и последовательно найти а_ь а затем я₀.

Продолжая подобным образом, можно найти коэффициенты полинома третьей, четвертой и вообще любой степени N. Так, например, для полинома третьей степени третья разность будет находиться так:

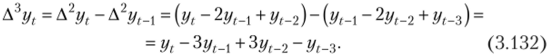
Средняя третьих разностей равна.

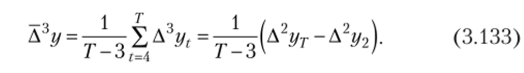
Эта разность в свою очередь характеризует третью производную функции, равную для параболы третьей степени 6а₃. Тогда коэффициент а_ъ можно найти так:

Очевидно, что трудоемкость такого способа нахождения параметров параболы (Т — 1)-й степени меньше, чем трудоемкость построения степенных функций (Т — 1)-й степени, при решении системы из Т уравнений с Т неизвестными коэффициентами, или трудоемкость разложения функций в степенные ряды Тейлора. Однако и его можно упростить, вычисляя лишь конечные разности, которые характеризуют конечные производные функций.

Таким образом, для оценки коэффициентов полиномов а_х, а₂ и «з найденные оценки производных с помощью конечных разностей делились для коэффициента на 1 (3.126), для коэффициента а₂ — на 2 (3.131), для коэффициента а₃ — на 6 (3.133) и т. п. В случае расчета оценок производных надобность в подобной процедуре умножения коэффициентов при показателях, возводимых в одинаковую степень, отпадает, что значительно упрощает расчеты. Кроме того, при расчете средних разностей сумму разностей необходимо было делить на число этих разностей. Без этой процедуры также можно обойтись. Действительно, если необходимо сравнить вторую производную данного ряда со второй производной другого ряда, то от умножения или деления каждой производной на одну и ту же константу, не равную нулю, результат отношения не изменится. Поэтому процедура еще более упрощается — следует находить не среднюю разностей, а просто их сумму. Сравнив формулы для вычисления конечных разностей (3.123), (3.128) и (3.132), легко обнаружить закономерность, с помощью которой можно сгенерировать формулу для вычисления конечной разности любого порядка. Но поскольку подобная задача уже решена применительно к интерполяционной формуле Ньютона, воспользовавшись этим, запишем формулу вычисления конечной разности п-го порядка в точке t:

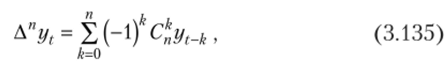
где k — порядковый номер члена разности (3.133); k = 1, 2, 3,п С — число всех сочетаний из п различных элементов по k, которое, как известно, находится по формуле:

в которой знак «!" — это знак факториала. Напомним, что по определению 0! = 1.

Сумма п-х конечных разностей, т. е. не усредненная оценка /7-й производной данного ряда, определяется по формуле:

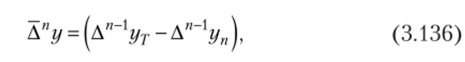
где А^п~^]У_т— последняя п-я конечная разность в ряду вычисляемых п-х конечных разностей для исходных значений y_t, т. е. п-я разность при t = Т; А^п~^{у_п — первая в ряду вычисляемых п-х конечных разностей, когда наблюдение t = п.

Поскольку любой прогнозист без труда может вычислить конечные разности (3.135), а на их основе — сумму этих конечных разностей (3.136), то для любых двух рядов y_t и х_р состоящих из Т наблюдений, можно получить (Т — 1) пар чисел:

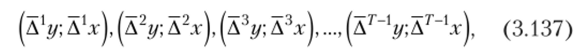
которые характеризуют первые, вторые, третьи и т. д. до (Т — 1)-й производные указанных рядов. С учетом того, что производные наилучшим образом характеризуют динамику процессов, сравнение указанных пар значений может характеризовать степень согласия в динамике рядов y_t и х_г Очевидно, что сравнение пар значений производных следует производить так, чтобы итогом данного сравнения стал некоторый расчетный коэффициент, имеющий ясное смысловое толкование. Сам коэффициент будет характеризовать согласие двух исходных рядов в динамике, поэтому его имеет смысл назвать именно так.

Чтобы предложить формулу вычисления коэффициента согласия в динамике, воспользуемся неравенством Коши, которое для конечных сумм имеет вид.

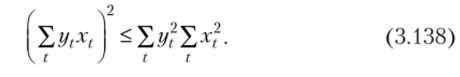
Если левую часть указанного неравенства разделить на его правую часть, будет получено выражение, которое никогда не будет больше единицы:

Равенство единице может быть только в том случае, когда ряд значений y_t представляет собой линейное преобразование ряда x_t.

Если вместо пар значений y_t и x_t подставить в предлагаемую формулу пары значений сумм конечных разностей (3.137) и извлечь квадратный корень из полученного выражения, то получим формулу, внешне напоминающую формулу для расчета коэффициента парной корреляции, который и назовем «коэффициент согласия в динамике»:

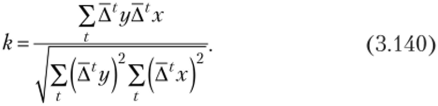
К этому коэффициенту можно будет применить толкование, аналогичное толкованию значений коэффициента парной корреляции.

Поскольку сумма разностей может быть как положительной, так и отрицательной, то и итоговое значение коэффициента согласия в динамике может быть как положительным, так и отрицательным. Для того чтобы понять, что именно отражает коэффициент согласия в динамике, представим, что ряды y_t и x_t находятся в линейной функциональной зависимости друг от друга, но под воздействием внешних по отношению к ним факторов меняются от наблюдения к наблюдению по сложному нелинейному закону. Поскольку они связаны друг с другом линейной функциональной зависимостью, их производные будут также линейно зависеть друг от друга, а неравенство Коши превращается в таком случае в равенство, поэтому коэффициент (3.140) будет равен единице.

Тогда можно утверждать, что в случае если значение коэффициента (3.140) близко по модулю к единице, динамика двух исходных рядов y_t и х_г находится в очень сильной степени согласия друг с другом, поскольку значения их производных разного порядка соответствуют друг другу. Согласованность их динамики свидетельствует о том, что между ними весьма вероятна взаимосвязь.

Если же вычисленное значение модуля коэффициента (3.140) близко к нулю, следует признать, что динамика двух рядов различна и наличие взаимосвязи между ними вряд ли возможно, ведь производные высших порядков рассогласованны, а это значит, что динамика одного ряда y_t не похожа на динамику другого ряда х₍ и его изменение вряд ли вызвано действием фактора, отражаемого рядом значений х_г В отличие от коэффициента парной корреляции, значение коэффициента согласия в динамике, близкое к нулю, однозначно указывает на то, что между двумя рядами взаимосвязи нет.

Так о чем же свидетельствуют значения коэффициента согласия в динамике, лежащие по модулю в пределах от 0 до 1? Для ответа на этот вопрос продемонстрируем использование данного коэффициента на условных данных.

Если ряд y_t представляет собой синусоиду, изменяющуюся во времени t> а ряд x_t — косинусоиду с той же амплитудой и фазой — y_t = sin t x_t = cos t, то для 100 точек, снятых в течение одного периода этих гармонических функций, коэффициент парной корреляции составит величину, равную г= -0,13 674, что свидетельствует об очевидном отсутствии линейной взаимосвязи. При этом, кстати, многие практикующие экономисты сделают вывод об отсутствии взаимосвязи между y_t и x_t вообще.

Коэффициент согласия в динамике дает величину, равную k = 0,9 796 672, что свидетельствует о наличии очень сильного соответствия в динамике показателей. Это означает, что у исследователя, получившего такое значение коэффициента согласия в динамике, есть все основания предполагать наличие взаимосвязи между факторами.

Из данного примера можно сделать следующий вывод: если для изучаемых рядов коэффициент парной корреляции по модулю близок к нулю, а модуль коэффициента согласия при этом близок к единице, это свидетельствует о наличии тесной нелинейной взаимосвязи между исследуемыми факторами.

Для подтверждения свойств коэффициента согласия в динамике для выявления возможной взаимосвязи между факторами проведем расчеты еще на одном примере, условные данные которого приведены в табл. 3.4.

Таблица 3.4

Условные данные для расчета коэффициента согласия в динамике.

Данные в этой таблице подобраны таким образом, чтобы резкий рост ряда x_t на четвертом наблюдении и его последующее падение вплоть до седьмого наблюдения могли бы быть причиной аналогичной динамики показателя y_t со сдвижкой во времени — показатель y_t растет на пятом наблюдении и начинает падение на следующем шаге вплоть до восьмого наблюдения (иначе говоря, между ними имеется лаг в единицу). Это отражено на графике рис. 3.9, который построен по данным табл. 3.4.

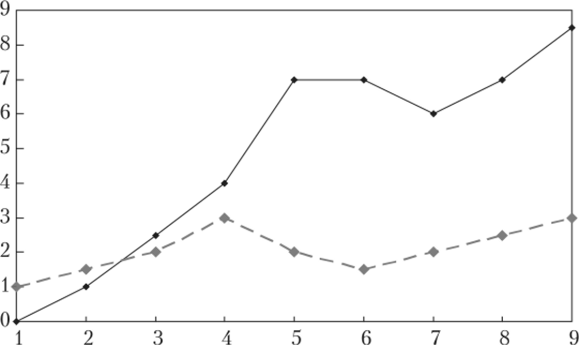
Рис. 3.9. Динамика условных рядов данных:

сплошная линия — ряд у прерывистая линия — ряд х

Расчеты коэффициента парной корреляции и коэффициента согласия в динамике для этих двух рядов показывают следующее. Коэффициент парной корреляции между анализируемыми рядами равен г = 0,5828, а коэффициент согласия в динамике — k = 0,9918.

Различие между этими коэффициентами довольно велико. Чтобы понять причину такого различия, обратимся к графику зависимости y_t от х₍ (рис. 3.10).

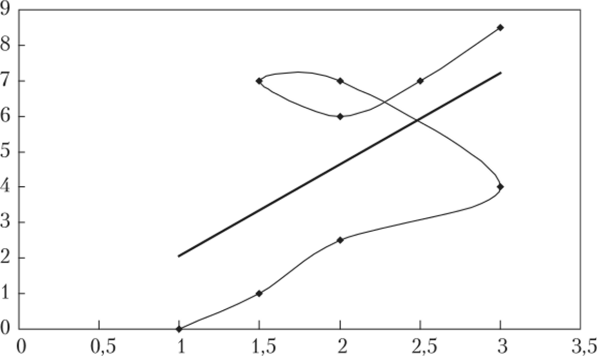
Рис. 3.10. Совместное изменение х и у во времени:

жирная линия по центру — прямая парной регрессии Как видно из графика, предположить наличие линейной зависимости между этими двумя рядами сложно, а именно наличие линейной корреляционной связи между случайными факторами и ищет коэффициент парной корреляции. Кроме того, если рассматривать эти два ряда так, как будто они засорены некоторыми случайными ошибками, и попытаться построить прямую линию, проходящую через них (она изображена на рисунке 3.10), можно убедиться в том, что ошибка аппроксимации такой линии будет очень высокой, что и демонстрирует значение коэффициента парной корреляции, равное 0,5828. Коэффициент парной корреляции не «уловил» возможную взаимосвязь между двумя рядами, а коэффициент согласия в динамике это сделал. Высокое значение коэффициента согласия в динамике по модулю выявляет наличие сложной взаимосвязи между рядами, которое формальный корреляционный анализ не подтверждает. Коэффициент согласия в динамике достаточно высок и свидетельствует о возможности обратной взаимосвязи между факторами, так как характеры динамики факторов близки друг к другу.

Для того чтобы установить вид взаимосвязи между факторами, необходимо осуществить дополнительные исследования, в том числе и расчет лагов между рядами посредством расчета кросс-корреляций. Проведем такое исследование. В табл. 3.5 приведены значения коэффициентов кросскорреляций между значениями х₍ и y_t+{.

Таблица 35

Условные данные для расчета коэффициента согласия в динамике.

В нашем условном примере было мало наблюдений, тем не менее, по значениям, показанным в табл. 3.5, можно заметить, что между рядом x_t и рядом у_п сдвинутым на 1, существует корреляция выше средней. Именно это мы и наблюдали по графику, это нам показал и коэффициент согласия в динамике.

Отсюда следует вывод: если для изучаемых рядов коэффициент парной корреляции мал, а модуль коэффициента согласия при этом близок к единице, это свидетельствует о наличии тесной взаимосвязи между исследуемыми факторами, возможно, нелинейной, а возможно — линейной с лагами.

Указанные примеры показывают, что предлагаемый коэффициент согласия в динамике действительно дает исследователю новую информацию, весьма важную для того, чтобы решить задачу определения степени взаимосвязи между факторами.

Таким образом, можно сделать вывод о том, что коэффициент согласия в динамике можно использовать в качестве дополнительного инструмента, позволяющего уточнить наличие взаимосвязи между факторами. Совместное иснользование сравниваемых коэффициентов дает прогнозисту значительно больше информации, чем простое использование каждого из них в отдельности. Коэффициент парной корреляции показывает исследователю, насколько тенденции двух изучаемых рядов совпадают в их линейном росте, а коэффициент согласия в динамике — насколько вариации одного показателя соответствуют вариациям другого.

Высокое значение модуля коэффициента согласия в динамике свидетельствует о том, что между изучаемыми факторами возможна тесная взаимосвязь. Если при этом коэффициент парной корреляции близок к единице, можно утверждать, что зависимость между факторами приближается к линейной. Если же коэффициент парной корреляции по модулю далек от единицы, прогнозисту необходимо осуществить дополнительные исследования для выявления формы взаимосвязи между изучаемыми случайными переменными.

• [1] Брюшипкип В. Н. Логика: учебник. М.: Гардарики, 2001. С. 262—269.
• [2] Светунъков С. Г. Количественные методы прогнозирования эволюционных процессов. Ульяновск: Изд-во УлГУ, 1997. С. 62—74.