Матричные элементы одно-и двухэлектронных операторов на функциях в виде определителей

Для дальнейшего построения теории на>" необходимо будет получить выражения для матричных элементов однои двухэлектронных операторов Л (1) и g (1, 2) = g (2, 1), а также для интегралов перекрывания на функциях в виде определителей:

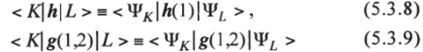
и.

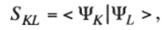
где функции Фди ф^ представляют собой нормированные детерминанты для системы N электронов, составленные из ортонормированных спин-орбиталей ф*.

Начнем рассмотрение с интеграла перекрывания:

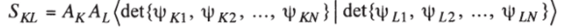
где, например,.

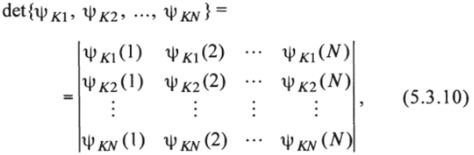
А_к и A_l- нормировочные множители перед детерминантами в Ф*- и Ф_Л, а дополнительный индекс К или L у спин-орбиталей подчеркивает их принадлежность тому или иному определителю. Разложим теперь тот и другой определитель по первому столбцу:

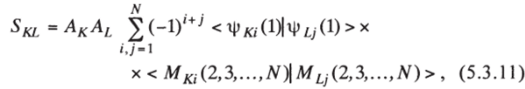
где М_к, и M_Lj — миноры, получаемые из исходных определителей вычеркиванием первого столбца и /- или у-й строки соответственно. Если ф^ = ф^, то интеграл = 1, в противном случае он равен нулю. Продолжая намеченный процесс последовательного разложения по первым столбцам миноров (ЛМ)-, (N-2)-ro и т. д. порядков, придем в конечном итоге к стоящим под знаком суммы произведениям вида.

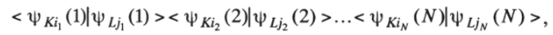
в каждом из которых встретится обязательно хотя бы один интеграл < ф/с," |ф/.;_п >, в котором Фк/_я * фц_п, если определители Ф^ и.

4*_t различаются хотя бы одной спин-орбиталью. Коль скоро такой интеграл равен нулю, то и каждое произведение в этом случае обращается в нуль, т. е. S_KL = 0. Если же оба определителя одинаковы (К = L), то в соотношении (11) интеграл < Ч'/а (1)1Ч^,к,' (1) > = 1 при / - у и равен нулю во всех остальных случаях. Поэтому (11) сведется к следующему выражению:

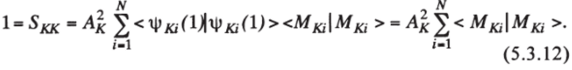
Вводя разложение определителей M/а (ЛМ)-го порядка вновь по первому столбцу, получим.

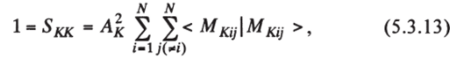
где М_К1) — минор (jV-2)-ro порядка, получающийся из исходного определителя вычеркиванием первого и второго столбцов и двух строк с номерами / и j. Суммирование по j ведется по всем тем значениям, которые не равны /. Продолжая этот процесс далее, в конце концов придем к минорам первого порядка, каждый из которых есть интеграл, равный единице. Число таких единиц будет равно числу всех возможных миноров первого порядка, которое без труда получается следующим образом: число миноров (AM)-ro порядка, а следовательно, и число членов в сумме (12) равно N (i= 1, 2,…, N); каждый из этих миноров дает N-1 миноров (,/V-2)-ro порядка, что приводит к числу членов в сумме (12), равному Л^(Л^-1); продолжение этого процесса увеличивает это число в N-2 раз, далее в N-3 раз вплоть до множителя N-(.N-1) = 1, так что полное число миноров первого порядка получается равным N (N-1)… 2*1 = ЛИ. Таким образом, A^(N) = 1, т. е. А_к = (N)~У^[1]. Нормированные определители.

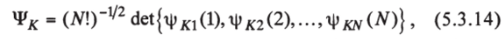
составленные из ортонормированных спин-орбиталей op_Ki, обычно называют детерминантами Слэтера по имени выдающегося американского теоретика Джона Слэтера^[2]. Запишем теперь выражения для матричных элементов (7) оператора й (1). Этот оператор действует только на функции, зависящие от переменных первого электрона. Поэтому, разлагая определители Слэтера Ч^ и Ч^ по первому столбцу, найдем:

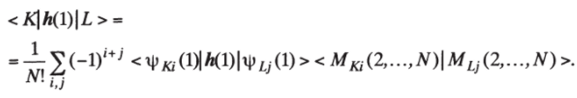
Миноры М_к, и M_L] суть определители (W-1)-го порядка, составленные из ортонормированных функций. Если M_Ki = M_L] или в крайнем случае отличается от него лишь порядком нумерации орбиталей, то интеграл < М_KiMц > - (N — 1)! (с точностью до множителя ±1). В противном случае этот интеграл равен нулю. В отличие же от того результата, который был использован при рассмотрении интеграла перекрывания, теперь уже нельзя утверждать, что интеграл должен обращаться в нуль при ф^ ^ф^. Поэтому возможны два случая, когда интеграл < Kh ()L > не равен нулю:

а) Ч^/_А. = Ф_; и тогда.

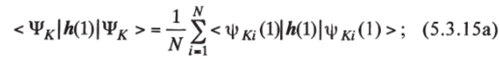
б) Ч^,_А— j* 4>_L, однако они различаются лишь одной орбиталью, например ф*-, * ф_ь (все же остальные орбитали в обоих определителях одинаковы); при этом.

Во всех остальных случаях матричный элемент < 4^,_JC|A (l)|4^;_i > обращается в нуль.

N

Для суммы одноэлектронных операторов ^ h (i) можно без труда установить, что для любого /.

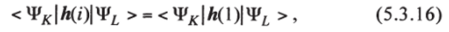
так что при нахождении среднего значения оператора Гамильтона (1) для всей системы электронов соответствующие матричные элементы вида (15а) и (156) должны быть просто умножены на число членов в этой сумме, т. е. на N. Для того, чтобы придти к соотношению (16), поступим следующим образом. Заменим в интеграле < Ч^,_х|й (г)|Ч^,? > переменные/-го электрона на переменные 1-го электрона, а переменные 1-го электрона — на переменные /-го электрона. При такой замене переменных интеграл не изменится, оператор А (/) перейдет в А (1), а функция Ч^ — в определитель вида.

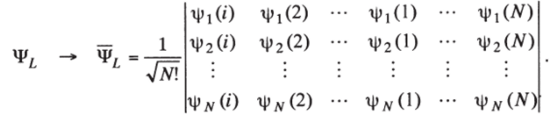
Эта запись показывает, что функция 4*_t отличается от 4^#_i лишь перестановкой двух столбцов: /- и 1-го. Из теории определителей хорошо известно, что такие два определителя отличаются друг от друга лишь множителем -1. Поэтому Чф = - 4^,_t, Ч^ = - Ч^, что и доказывает справедливость соотношения (16).

Аналогичные рассуждения могут быть выполнены и для матричных элементов двухэлектронных операторов g (l, 2). Не останавливаясь на них подробнее и оставляя их в качестве задач, окончательно можно выписать соотношения, которые называются правилами Слэтера для матричных элементов однои двухэлектронных операторов. Если обозначить через Ц/J определитель Слэтера Ч¹, в котором спин-орбиталь заменена на спин-орбиталь зр_у, а через — определитель Слэтера 'Р, в котором зр_; и зр* заменены на зр₇ и зр, соответственно, то правила Слэтера будут иметь вид:

а) для одноэлектронного оператора А = %h (i)

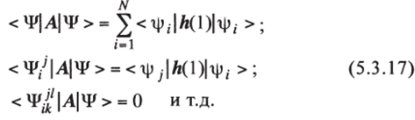
для определителей, отличающихся от Ч* заменой трех и более спинорбиталей;

б) для двухэлектронного оператора В = У g (i, j)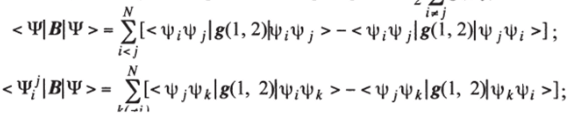

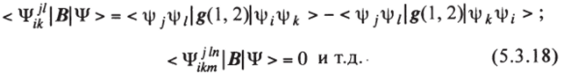
Во всех интегралах в правых частях соотношений (18) как слева, так и справа от символа оператора g (1, 2) на первом месте стоит функция, зависящая от переменных первого электрона, на втором — функция, зависящая от переменных второго электрона. Так например,.

<

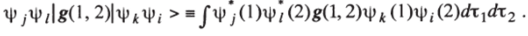
• [1] известны его монографии, часть из них переведена на русский язык (см. стр.510).
• [2] Слэтер Джон, один из создателей квантовой механики молекул и квантовойхимии, работавший в США. Его именем названы однодетерминантные волновыефункции, один из вариантов метода самосогласованного поля, атомные орбитали, используемые в качестве базисных при молекулярных расчетах и т. д. Хорошо