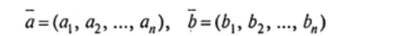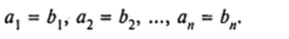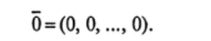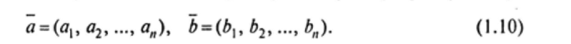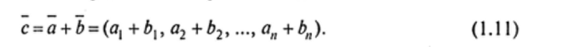Векторное пространство. 
Математика в экономике

Понятие и основные свойства векторов

Ранее мы рассмотрели векторы в двумерном и трехмерном евклидовом пространстве (параграф 1.1). Здесь мы приведем обобщение соответствующих понятий на л-мерный случай.

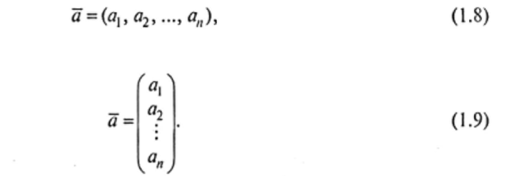
Определение 3. Любой упорядоченный набор из л действительных чисел a_v а_2У …, а_п называется п-мерным вектором а числа, составляющие упомянутый набор, называются координатами (компонентами) вектора а.

Определение 4. Совокупность всех л-мерных векторов называется п-мерным векторным пространством /?" .

Координаты л-мерного вектора а можно расположить либо в строку либо в столбец Запись вида (1.8) называется вектором-строкой, а вида (1.9) — вектором-столбцом.

Определение 5. Два вектора с одним и тем же числом координат 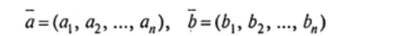называются равными, если их соответствующие координаты равны, т. е.

Определение 6. Вектор, все координаты которого равны нулю, называется нулевым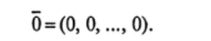

Операции над векторами

Пусть векторы а и Ь принадлежат л-мерному векторному пространству.

Будем называть суммой векторов а и b вектор с, координаты которого равны суммам соответствующих координат векторов а Ъ

Пусть X — любое действительное число. Произведением вектора, а на чиаю X будем называть вектор, координаты которого получаются умножением соответствующих координат вектора а на это число:

Из введенных таким образом операций над векторами вытекают следующие свойства этих операций. Пусть а, Ьнс — произвольные векторы л-мерного векторного пространства, тогда:

• 1) a+b=b+a — переместительное свойство;
• 2) (a + b) + c = a + (b + c) — сочетательное свойство;
• 3) X (a + b)=Xa + Xb, где X — действительное число;
• 4) (X + р) я = Ха + ря, где X и р — действительные числа;
• 5) Х (ря) = (Хр)я, где X и р — действительные числа;
• 6) я+ 6 = а;
• 7) для любого вектора я существует такой векторя, чтоя = (-1)я, д + (-а)=0;
• 8) 0я = 0 для любого вектора я.

Определенное л-мерное векторное пространство /?" является линейным, поскольку для него выполняются свойства линейности:

• 1) для любых двух векторов а и b из Л" их сумма также принадлежит Rⁿ
• 2) для любого числа, а и вектора а е R" вектор, а а принадлежит R" .

Определение 7. Пусть U — подмножество линейного пространства Rⁿ. Оно называется линейным подпространством Rⁿ, если для любых векторов а и b из U и любого числа, а выполнены свойства линейности 1и2ив +^иоиг принадлежат подмножеству U.

Например, совокупность всех векторов я, таких, что сумма их координат равна нулю (я, + я₂ + … + а_п — 0), образует линейное подпространство R" .