Понятие дифференцируемости функции

Как уже говорилось, полным приращением функции /(Л/) в точке Л/(х_р х₂,…"х_т), соответствующим приращениям Дх_р Дл^,…" Дх_т, является разность.

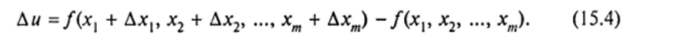
Определение 2. Функция и = /(А/) называется дифференцируемой в точке Л/(х, х₂, …, х_т), если ее полное приращение (15.4) в этой точке можно представить в виде.

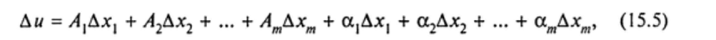
где Л, А₂, …, А_т — некоторые нс зависящие от Ах, Дх₂, …" Дх_т числа, а а, (Xj,…, а_т — бесконечно малые функции соответственно при Ах, —> 0, Дх₂ —> 0,…" Дх —> 0.

/и Условие (15.5) называется условием дифференцируемости функции в данной точке М евклидова пространства Е^т. Если хотя бы одно из чисел Л, Л₂, …, А_т отлично от нуля, то сумма.

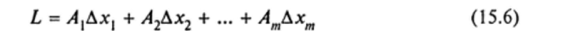
Рис. 15.1.

является главной линейной частью полного приращения дифференцируемой функции относительно приращений аргументов.

Приведем необходимые условия дифференцируемости функции нескольких переменных.

Теорема 15.1. Если функция иf{M) дифференцируема в точке Л/(х, х₂, …, х_т), то она имеет в этой точке частные производные по всем аргументам, причем — -А/, где А. определены из условия (15.5).

Эх,.

откуда.

Доказательство. Из условия (15.5) следует, что частное приращение функции в точке М равно:

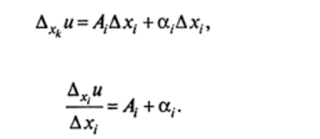
Так как а_у -> 0 при Ах -> 0, предел левой части этого равенства равен А_г что и требовалось доказать. ?

Рассмотрим функцию р = ^Дх,² + Д*2 + — + которая является бесконечно малой при Ах, —> 0, Дх₂ —" 0,Ах_т —> 0. Поскольку |ДХ;|/р < I, имеем:

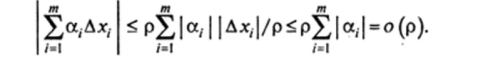
Следовательно, условие дифференцируемости функции нескольких переменных в данной точке М в силу теоремы 15.1 может быть записано в форме:

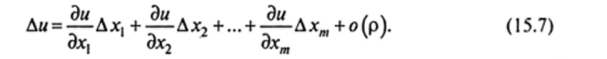
Далее приведем важную теорему о связи между дифференцируемостью функции нескольких переменных и ее непрерывностью.

Теорема 15.2. Если функция и = ДМ) дифференцируема в некоторой точке Л/, то она непрерывна в этой точке.

Доказательство. Из условия дифференцируемости (15.5) функции ДМ) следует, что выполнено условие (14.14) определения непрерывности функции в точке, т. е. Аи -" 0 при Ax_f. -> 0, / = 1,2, …, m, что и требовалось доказать. ?

Достаточные условия дифференцируемости функции нескольких переменных даются следующей теоремой.

Теорема 15.3. Если функция и = ДМ) имеет частные производные по всем аргументам в некоторой окрестности точки Л/, причем эти производные непрерывны в самой точке М, то данная функция дифференцируема в точке Л/. Доказательство этой теоремы мы опускаем; скажем только, что оно основано на использовании формулы Лагранжа для частных приращений функции по каждому аргументу. ?

Из теоремы 15.3 выводится важное следствие: непрерывность функции вытекает из непрерывности ее частных производных. Поскольку непрерывность функции нескольких переменных проверить напрямую бывает довольно трудно, это важное свойство функции можно установить более простым способом, проверив непрерывность ее частных производных.

Условие дифференцируемости функции двух переменных z = /(х, у) имеет геометрический смысл. Определим касательную плоскость к некоторой поверхности.

Определение 3. Плоскость, проходящая через точку N₀ поверхности, называется касательной плоскостью в данной точке, если угол между этой плоскостью и секущей, проходящей через точку N₀ и любую точку N на поверхности, стремится к нулю, когда точка N стремится по этой поверхности к точке N₀.

Если в точке N_Q поверхности существует касательная плоскость (рис. 15.2), то касательная в точке Д₀ к любой кривой, расположенной на этой поверхности и проходящей через точку /V₀, находится в касательной плоскости в данной точке к поверхности.

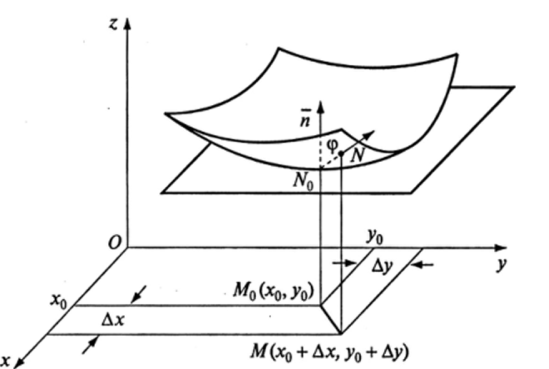
Рис. 15.2.