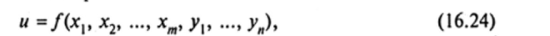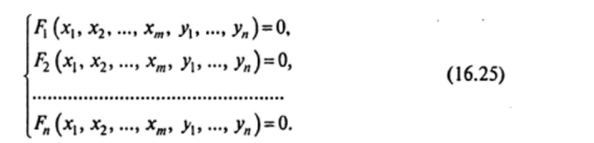Условный экстремум. 
Математика в экономике

Понятие и постановка задачи условного экстремума

В различных приложениях часто встречается задача нахождения экстремумов функции нескольких переменных при наличии дополнительных условий связи на ее аргументы. Такие экстремумы называют условными. Например, пусть требуется найти экстремум функции и = х² + у², если ее аргументы удовлетворяют условию связи х + у — 2 = 0. Экстремумы данной функции ищутся не на всей плоскости Оху, а только на прямой х + у — 2 «0 (рис. 16.1). Подставим в уравнение функции выражение для у из условия связи и тем самым сведем исходную задачу об условном экстремуме функции и = х² + у² к задаче отыскания безусловного экстремума функции и = 2х² — Ах + 4. Эта функция имеет экстремум в точке х = 1, т. е. функция и = х² + У² при наличии указанной связи имеет условный минимум и = 2 в точке (1, 1), который не совпадает с безусловным минимумом параболоида вращения в точке (0, 0).

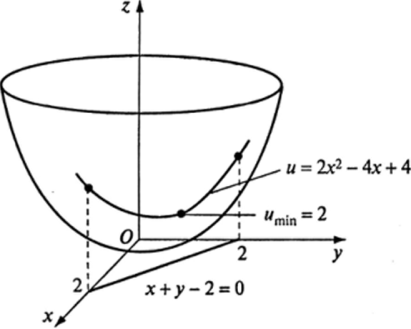
Рис. 16.1.

Задачи на условный экстремум возникают, в частности, при отыскании экстремума функции в замкнутой ограниченной области, когда условием связи на аргументы функции является уравнение границы области ее задания (см. п. 15.3.3 и 15.3.4).

Рассмотрим общую постановку задачи нахождения условного экстремума. Пусть задана функция т + п переменных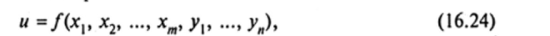

для которой нужно найти условный экстремум при наличии п условий связи:

Будем говорить, что функция (16.24) имеет условный экстремум при наличии связей (16.25) в точке Л/₀ (xf, xj,…, х°, у,⁰,…, координаты которой удовлетворяют условиям связи (16.25), если существует такая окрестность точки Л/₀, для которой значение функции (16.24) в точке М₀ является наибольшим (наименьшим) для всех точек, координаты которых удовлетворяют условиям связи (16.25).