Существование обратной функции

Теорема 16.1 может быть применена для установления условий, при которых функция у = /(х) имеет в некоторой окрестности точки х₀ обратную функцию х = /^_,(у), определенную в некоторой окрестности точки у₀ = /(х₀). Представим функцию у = / (х) в виде функционального уравнения F (х, у) =/(х) — у = 0. Если в этом выражении х является функцией от аргумента у, то по условию теоремы 16.1 мы получим следующее утверждение: если функция у —/(х) имеет в некоторой окрестности точки х_э отличную от нуля производную, то существует функция х- /^_1(у), определенная и дифференцируемая в некоторой окрестности точки у₀, где У₀ = f (х₀). Производная этой обратной функции согласно формуле

(16.7), в которой х и у нужно поменять местами, равна 1//'^/(х₀).

Теперь определим обратную вектор-функцию по отношению к векторфункции иf (xУ Рассмотрим случай, когда размерности векторов //их равны (см. п. 15.3.4). Образуем неявную вектор-функцию.

Тогда вопрос о существовании обратной вектор-функции х = / '(и) связан с вопросом о разрешимости векторного функционального уравнения (16.16). Найдем производную вектор-функции F по вектору и из уравнения (16.16) имеем: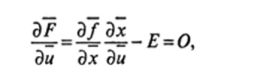

где Е — соответственно единичная и нулевая матрицы, Э//Эх — матрица Якоби (15.53). Умножая обе части этого равенства на матрицу, обратную матрице (15.53), получаем, что матрица Якоби для производной вектор-функции х по вектор-аргументу и выражается соотношением:

Как следствие теоремы 16.3 справедливо следующее утверждение, которое можно трактовать как теорему об обратной вектор-функции.

Если вектор-функция // = /(*) имеет невырожденную матрицу Якоби (15.53).

в некоторой окрестности точки х₀, то для этой функции существует обратная функция x-f '(//), которая определена и дифференцируема в некоторой окрестности точки //₀, где ио = /(до). Матрица Якоби для этой обратной функции равна обратной матрице для (15.53).