Дискретные модели популяций с неперекрывающимися поколениями

До сих пор мы рассматривав развитие популяции в непрерывном времени, при этом численность популяции являлась непрерывной функцией — решением дифференциального уравнения. Это правомерно, когда численность популяции можно аппроксимировать непрерывной кривой, что возможно лишь для достаточно многочисленной популяции.

Реально численность представляет собой дискретную величину, которая принимает некоторые значения в фиксированные моменты времени. Формализм, учитывающий дискретность численности популяции, больше соответствует экспериментальным данным по переписи реальных популяций (лабораторных или естественных), которая осуществляется в дискретные моменты времени. Если при этом предположить, что численность N зависит от численностей в некоторые предшествующие моменты времени, то для описания динамики численности популяций можно применять аппарат разностных уравнений.

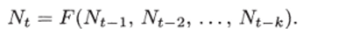
Если внешние и внутренние факторы, определяющие развитие популяции, остаются со временем неизменными, то численность популяции в момент времени t может быть описана при помощи разностного уравнения в виде:

Здесь функция F зависит от численности популяции в к предшествующие моменты времени.

Особенно просто выглядит разностное уравнение в случае, когда численность каждого следующего поколения в популяции N_t+1 зависит лишь от предыдущего поколения JV*. Это справедливо для многих видов насекомых. Их взрослые особи живут непродолжительное время, достаточное для откладывания яиц, и к моменту появления на свет нового поколения (на стадии взрослой особи) предшествующее поколение прекращает свое существование. То же имеет место для некоторых видов рыб, зоопланктона, птиц. Для таких популяций поколения не перекрываются, и уравнение (2.2.1) может быть записано в виде:

Опыт показывает, что в таких системах при малых численностях N растет от одной генерации к другой, а при высоких — падает. Это свойство — резко расти при малых N и падать при больших — в экономике проявляется как закон «бумов» и «спадов». В таких случаях функция F — одноэкстремальная, ее вид изображен на рис. 2.8.

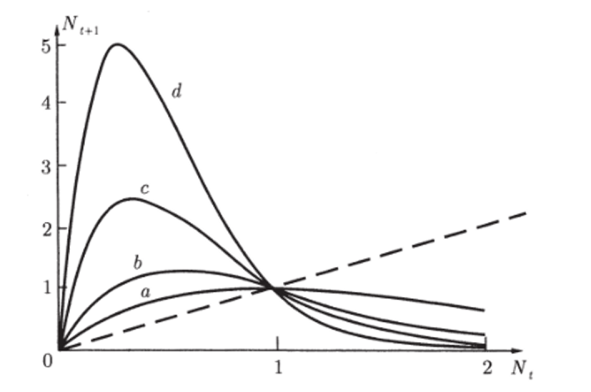
Рис. 2.8. Вид одноэкстремалыюй функции Nt+i = F (N_t).

В зависимости от крутизны графика функции F (N_t) (кривые а, Ь, с, d) в системе могут возникать самые разнообразные режимы: монотонное и колебательное приближение к состоянию равновесия, удаление от него, устойчивые колебания, квазистохастическое поведение (хаос). Модели вида (2.3.1) являются простейшими детерминированными объектами, демонстрирующими хаотическое поведение.

В гл. 4 мы увидим, что таким поведением могут обладать переменные в непрерывных автономных нелинейных системах трех и более дифференциальных уравнений. Таким образом, стохастичность может быть свойством, присущим самим природным системам, и не зависит от того, каким математическим аппаратом, непрерывным или дискретным, мы пользуемся.

Если поколения популяции в значительной мере перекрываются, допущение о зависимости Nt+i лишь от Nt уже несправедливо. В этом случае популяцию можно подразделить на дискретные возрастные классы (или стадии развития), численности которых зависят от численностей предшествующих (а в отдельных случаях и всех остальных) возрастных классов. Задача описания динамики возрастных классов таких популяций приводит к матричным (также дискретным) моделям, на которых мы остановимся ниже. Здесь мы рассмотрим пример модели популяции с неперекрывающимися поколениями разностный аналог логистического уравнения.

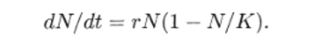
Заменим dN/dt на AN/At, где AN = N_t+i — N_t — разность численностей в последовательные моменты времени, At, = 1. Получим:

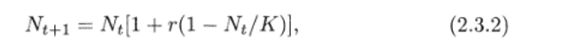
где параметры г и К имеют тот же смысл. Однако если в какой-то момент времени значение численности становится больше определенной величины

уравнение (2.3.2) дает отрицательное значение Nt+i- Это связано с видом функции f (Nt) = 1 4- r (l — Nt/K), изображенной на рис. 2.9а. Таким образом, уравнение (2.3.2) биологически не корректно. Отметим, что непрерывный аналог логистического уравнения свободен от этого недостатка, так как в нем при стремлении функции f (N) = г (1 — N/K) к нулю стремится к нулю и скорость возрастания N: dN/dt.

Для того чтобы исправить недостаток уравнения (2.3.2), следует взять в качестве f (N_t) функцию, асимптотически стремящуюся к нулю.

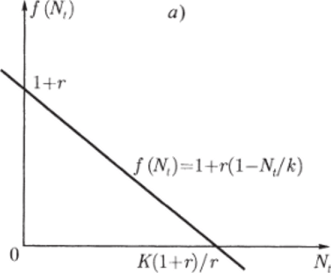
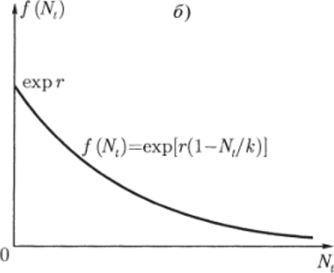
Рис. 2.9. Вид функции f (N_t) для дискретного аналога логистического уравнения: а — f{N_t) = г (1 — Nt/K); б — f (N_t) = exp{r (l — N_t/K)}.

при Nt —? оо. В частности, может быть выбрана функция ехр{г (1 — — N_t/K)}, изображенная на рис. 2.96. Уравнение.

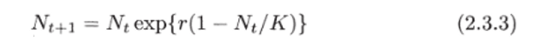
может быть рассмотрено в виде разностного аналога логистического уравнения. Такая экспоненциальная форма была предложена Мораном для численности насекомых и Рикером для рыбных популяций.

Ход решения может быть наглядно продемонстрирован графически при помощи гак называемой диаграммы и лестницы Ламерея (рис. 2.10). Если изобразить на одном графике зависимость правой и левой частей уравнения (2.3.3) от N, будем иметь картину, приведенную на рисунке: прямая N — биссектриса координатною угла и функция F (N) = Nexp{r (l — N/K)}, имеющая максимум. Точка их пересечения представляет собой равновесное состояние системы, аналогичное стационарному состоянию дифференциального уравнения (рис. 2.10 а).

На рис. 2.106 проиллюстрирован способ нахождения значений N_t в последовательные моменты времени. Пусть в начальный момент времени N = JV₀— Значение F (No) задает величину N в последующий момент времени t = 1. JVj, в свою очередь, определяет F (A'i) и, следовательно, N2 и т. д.

На рис. 2.11 а изображен случай, когда траектория сходится к равновесному состоянию, совершая затухающие колебания, на рис. 2.11 б — монотонное стремление численности Nt к равновесному состоянию.

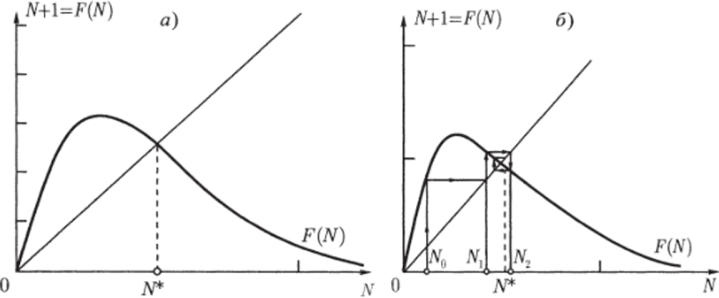
Рис. 2.10. Определение равновесного состояния в дискретной модели популяции с неперекрывающимися поколениями. Диаграмма и лестница Ламерея. N* — равновесная численность.

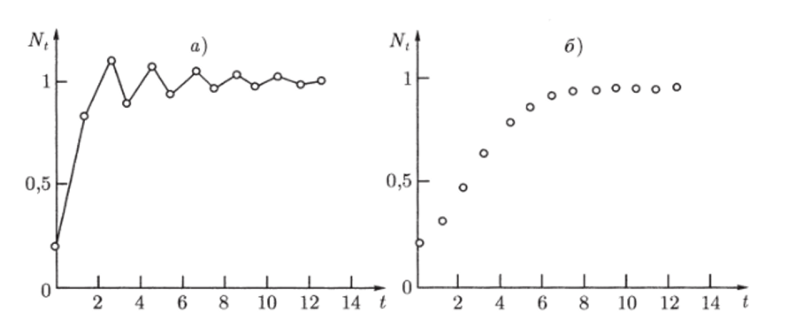
Рис. 2.11. Типы стремления численности к равновесному состоянию в модели (2.2.3).

К разностному уравнению применимы понятия, употребляемые при работе с дифференциальными уравнениями. Решением или траекторией уравнения (2.3.1) является любая последовательность значений {} (t = 0, 1, …), удовлетворяющая данному разностному соотношению при каждом t. Различным начальным значениям No соответствуют разные решения. Устойчивость решений можно определить так же, как устойчивость по Ляпунову решений дифференциальных уравнений: при достаточно малых отклонениях начального значения новое решение мало отличается от исходного.

Равновесием называется решение вида N_t = const = АТ*, удовлетворяющее соотношению Если решение (2.3.4) устойчиво, его называют устойчивой точкой. В общем случае равновесие возможно, если уравнение (2.3.4) имеет хотя бы один положительный корень N* (рис. 2.10).

Как и в случае дифференциального уравнения, для исследования устойчивости равновесия применим линейный анализ. Положим N_t = = N* + xt и линеаризуем уравнение (2.3.2), разлагая F в ряд по степеням Nt — N* = xt и отбрасывая члены порядка х и выше. Получим:

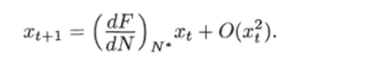
Из условий сходимости геометрической прогрессии следует, что Xt —? 0 при f —> оо, если dF/dNs" < 1, и x_t —? оо при t —> оо, если dF/dNjsf > 1. Эти условия и определяют устойчивость равновесия N* системы. Случаи dF/dNjy = 1 и dF/dN = 0 требуют дополнительного исследования членов более высокого порядка в разложении.

Можно сделать также некоторые заключения о характере приближения (или удаления) решений от равновесия. А именно в случае устойчивого равновесия, при.

отклонения от равновесия уменьшаются монотонно. Если.

то имеют место затухающие колебания вокруг N*. Если равновесие неустойчивое, при

отклонение от равновесия монотонно растет, а при.

удаление от равновесия происходит в виде нарастающих колебаний.

Для изучаемого нами уравнения (2.3.3) равновесие находится из выражения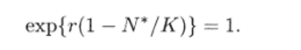

Очевидно, что единственное равновесное значение N* = К > 0 существует при любом г. Условия (2.3.5), (2.3.6) показывают, что устойчивая точка имеет место, если 0 < г < 2, при этом N_t —> N* монотонно при 0 < г < 1 и колебательным образом при 1 < г < 2.

Если г 2, из условий (2.3.7), (2.3.8) следует, что равновесие неустойчиво.

Построив функцию Ляпунова V* = (Nt — К)², можно показать, что при 0 < г < 2 равновесие N* = К глобально асимптотически устойчиво (Свирежев, Логофет, 1978, с. 47).

Разностные уравнения могут иметь и более сложные решения, например, в них возможны циклы (рис. 2.12), являющиеся аналогами предельных циклов для систем дифференциальных уравнений. Решение {N?} уравнения (2.3.1), состоящее из конечного набора Т значений, повторяющихся в строгой последовательности (т. е. = N^_+T, t = 0, 1, 2, …; ф AT_t*, j = 1, 2, …, Т — 1), называется циклом длины Т (Т — точечный цикл). Изучаемое нами уравнение (2.3.3) демонстрирует двухточечные циклы при 2 < г < r = 2,526, а при дальнейшем возрастании значений параметра г встречаются устойчивые циклы периода 4, 8, 16, …, 2к. Циклическое поведение численности N_t показано на рис. 2.12 а, б.

Разностное уравнение (2.3.3) наряду с равновесием и циклами может иметь хаотические решения, не стремящиеся ни к какому притягивающему решению. При этом существует связь между существованием циклов периода три и хаотических режимов. Можно показать, что, если уравнение обладает трехточечным циклом, оно также имеет решения любого периода, и существует несчетное множество начальных значений iVo, при которых решение не стремится ни к одному из этих циклов, т. е. хаотично. Поведение решения разностного уравнения (2.3.3) в этом случае принципиально зависит от начального значения No. Графический анализ показывает, что при г > г_с = 3,102 существуют два различных трехточечных цикла, а при г <�г_с трехточечных циклов нет. Следовательно, решения находятся в хаотическом режиме, когда г > г_с (рис. 2.13а, б).

Таким образом, задавая различные значения параметра естественной скорости роста г и начальной численности популяции iV₀, можно получить качественно различные типы поведения переменной N_t,.

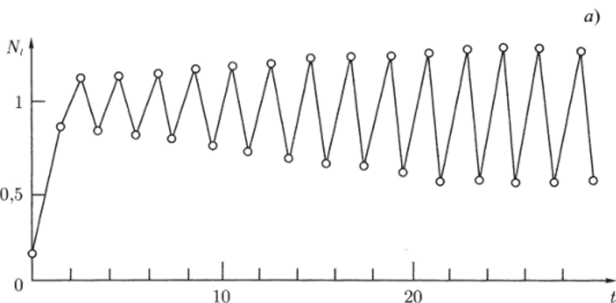
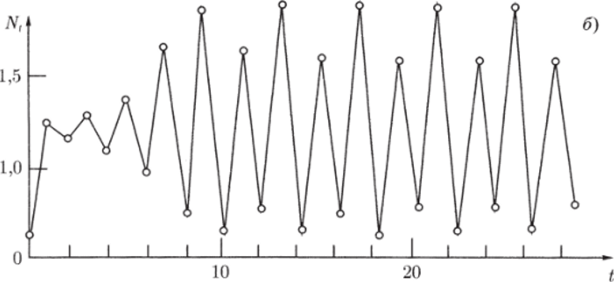
Рис. 2.12. Циклическое поведение решения уравнения (2.2.3): а — двухточечный цикл; б — четырехточечный цикл удовлетворяющие разностному уравнению (2.3.3). Строгое аналитическое исследование областей существования этих режимов проведено в (Свирежев, Логофет, 1978). Богатый спектр поведения траекторий содержит устойчивое равновесие, устойчивые циклы любой длины и хаотический режим, тип которого зависит от начальных условий (см. рис. 2.11−2.13).

Помимо (2.3.2) для описания динамики численности популяций с неперекрывающимися поколениями используют и другие уравнения.

Часто в качестве дискретного аналога логистического уравнения используется более простая форма:

Рис. 2.13. Примеры хаотических решений для уравнения (2.2.3): аколебания вокруг неустойчивого равновесия N* = 1 попадают, начиная с t = 23, в окрестность 3-точечного цикла, цикл также неустойчив; б — хаотическая траектория Здесь плотность популяции выражена в безразмерном виде, правая часть принимается равной нулю при t > 1. Параметр а определяет наклон графика функции правой части. На рис. 2.14 показаны диаграммы Ламерея и динамика численности во времени для разных значений параметра а в уравнении (2.3.9). В случае не очень сильной нелинейности (а < 3) численность популяции стремится к устойчивому состоянию равновесия (рис. 2.14 а, б). Когда график F (N_t) становится.

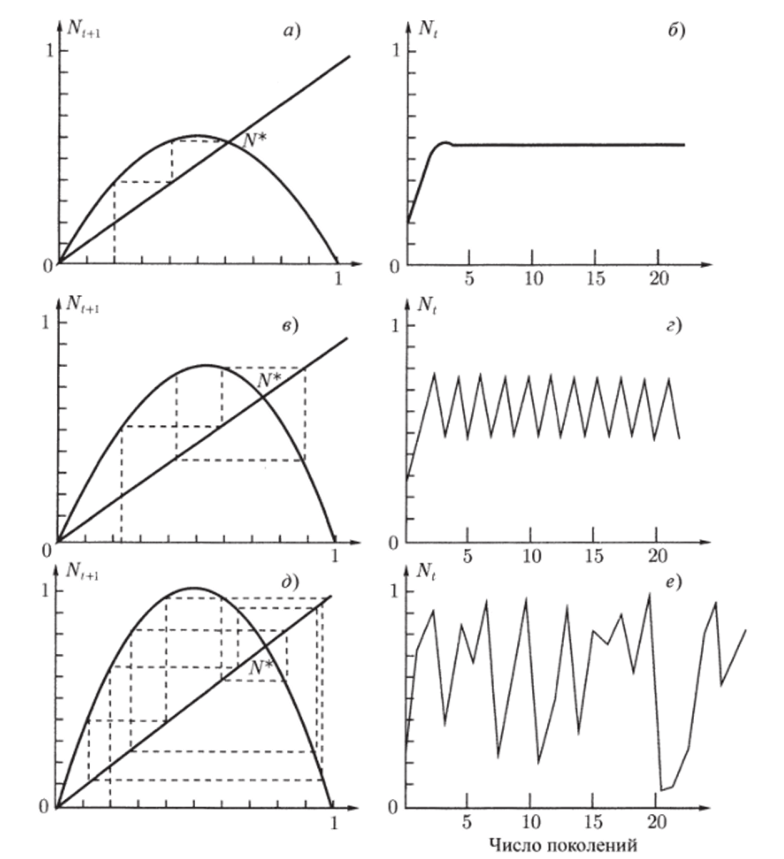
Рис. 2.14. Вид функции F (Nt) для разных значений параметра уравнения (2.3.9) и соответствующие зависимости численности от времени: а, б — монотонное приближение к равновесию; о, г — цикл; д, е — хаос более крутым, устойчивое равновесие переходит в устойчивые циклы (см. рис 2.11 в, г). По мере увеличения максимума функции F (N_t) длина цикла растет и значения численности повторяются через каждые 2, 4, 8, …, 2п поколений. При значениях параметра а > 3,570 происходит хаотизацня решений (рис. 2.14д, е).

Аналогичными свойствами обладает уравнение.

которое хорошо описывает динамику численности 28 видов сезонно размножающихся насекомых с неперекрывающимися поколениями (Hassel, 1976). На рис. 2.15 показаны области параметров /?, Л, где реализуются различные типы поведения.

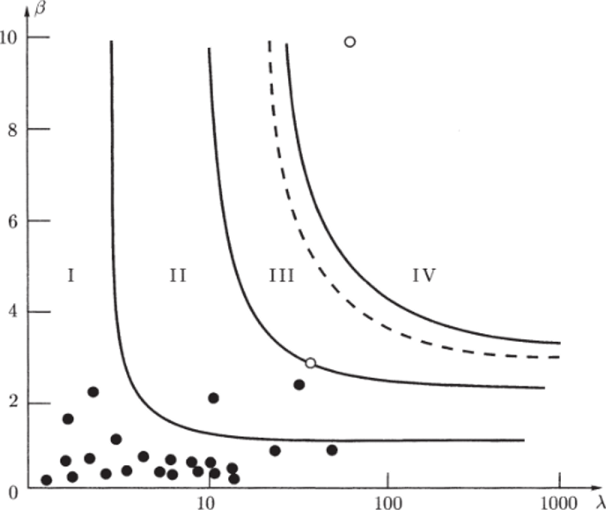
Рис. 2.15. Области значений параметров /3, Л для уравнения (2.3.10) с различным характером поведения: I — монотонное стремление к равновесию; II — затухающие колебания; III — устойчивый цикл; IV — хаос. Пунктиром отделена область циклов с периодом 2 и периодом 2ⁿ, п > 1. Заштрихованные кружки — значения параметров для естественных, пустые — для лабораторных популяций (Hassel, 1976).

Интересно, что некоторые достаточно просто измеряемые характеристики популяций, демонстрирующих хаотическое поведение, имеют регулярный характер. В этом смысле, чем хаотичнее поведение популяции, тем оно более предсказуемо. В работе (Vandermeer, 1982) показано, что если функция F (N_t) в уравнении (2.3.1) имеет один экстремум и падающая часть ее графика имев!' точку перегиба, то чем больше амплитуда вспышки численности, тем длительнее интервал малых численностей популяции.

Для случая линейного роста при малых N:

и экспоненциального спада при больших N:

амплитуда вспышки прямо пропорциональна времени между вспышками. Зависимости размера вспышки от продолжительности периодов малой численности имеют вид прямых (рис. 2.16).

Отметим, что решение разностных уравнений лежит в основе моделирования любых реальных биологических процессов, в особенности экологических. Богатство динамического поведения модельных траекторий разностных уравнений является основой их успешного применения для описания сложных природных явлений. При этом ограниченность параметрических областей существования определенного типа решений может служить дополнительным основанием для оценки адекватности предлагаемой модели.