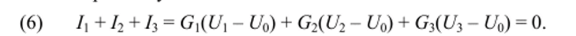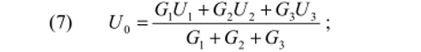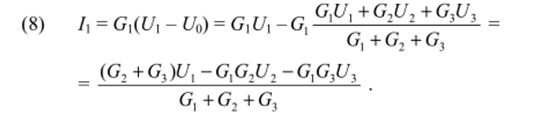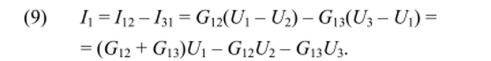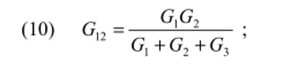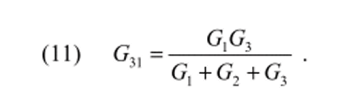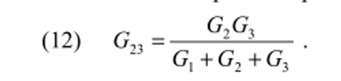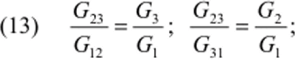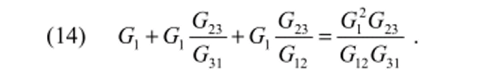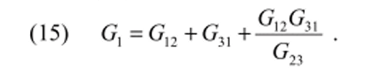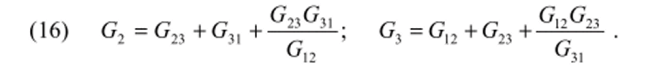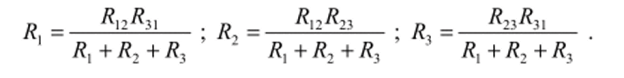Последовательно-параллельное соединение. 
Электротехника и электроника

Особенности преобразования комбинированных цепей со смешанным (последовательным и параллельным) соединением резистивных элементов рассмотрим на примере схемы, приведенной на рис. 4, а. Эквивалентная (ре;

зультирующая) проводимость Gi 1 (рис. 4,6) определяется в такой последовательности:

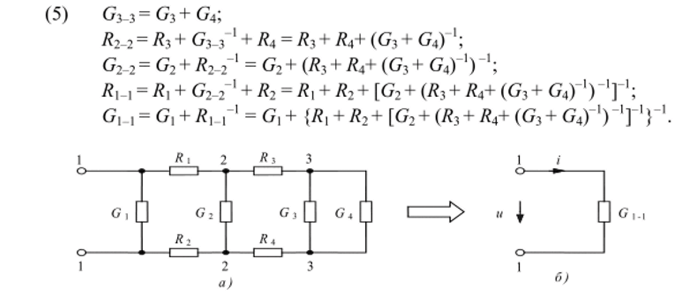
Рис. 4. Преобразование смешанной цепи.

Отметим, что можно получить выражения (5) только с проводимостями, если обозначить R = G, или только с сопротивлениями, если обозначить G = R^l. Однако использование гибридных обозначений резисторов упрощает запись соотношений (5).

Преобразование трехполюсных цепей.

При расчете электрических цепей часто бывает полезным преобразовать звезду в треугольник или треугольник в звезду. На рис. 5, а приведен двухполюсник 1−1 с внутренней структурой звезда-треугольник. Путем преобразования звезды в треугольник (рис. 1,6) можно легко определить значение проводимости (сопротивления) между полюсами 1 — 1 и представить исходную цепь в виде двухполюсника (рис. 1, в).

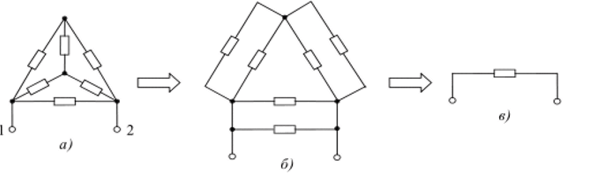
Рис. 5. Исходная цепь звезда-треугольник (а); цепь после преобразования звезды в треугольник (б); цепь после преобразования треугольника в двухполюсник (в) Для нахождения взаимосвязи между проводимостями трехполюсных цепей воспользуемся схемами на рис. 6. Различие между схемами стира;

ется при равенстве напряжений и токов трехполюсных цепей. Это условие и будет использовано в дальнейшем.

Преобразование звезды в треугольник. Для этого случая необходимо проводимости G_]2, G₂₃, G_3] треугольника выразить через проводимости G_b G₂, G₃ звезды. Для звезды (рис. 6, а) суммарный ток равен нулю: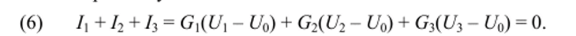

Из (6) находим.

После подстановки (7) в (6) находим.

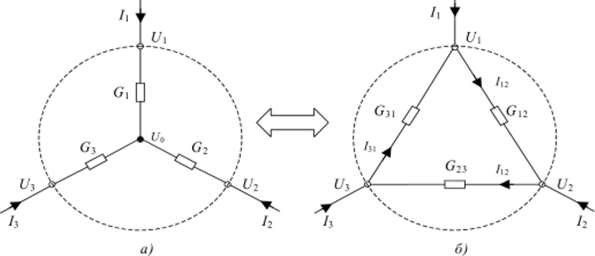
Рис. 6. Соединение резисторов по схеме звезда (а) и треугольник (6).

Для треугольника ток.

По условию в обеих схемах токи /1 должны быть равными при любых одинаковых напряжениях U₉ и_ъ ?У₃. Поэтому, приравняв коэффициенты при U_2y ?/₃ правых частей выражений (8) и (9), получим.

Подобным образом определяется третья проводимость.

Отмстим, что в соотношениях (10)—(12) индексы проводимостей G_kl треугольника соответствуют индексам проводимостей G_k, G/ звезды.

Преобразование треугольника в звезду. Для этого случая необходимо проводимости G_n звезды выразить через проводимости Gu треугольника, что достигается решением системы уравнений (10)—(12). Разделим (12) на (10) и (11).

Определив из (13) G₃, G₂ и подставив в (12), получим.

Из (14)находим.

Подобным образом определяются другие проводимости.

Учитывая, что G = 1//?, можно записать соотношения (15), (16) в следующим виде: