Функция полезности. 
Теория принятия решений. 
Том 2

Субъективные вероятности, рассмотренные ранее, являются фактически численным выражением мнения ЛПР и информации, которой он владеет. Понятие полезности, вводимое далее в этом параграфе, служит для численного выражения вкусов и предпочтений ЛПР. Современная экономическая теория изучает предпочтения с точки зрения их рациональности. Принятый в ней аксиоматический подход состоит в том, что критерии математически выводятся из наборов условий (аксиом), накладываемых на предпочтения.

Обратите внимание!

Теория ожидаемой полезности, возникшая еще в XVII в., получила обоснование при помощи аксиомы независимости в XX в. Данная аксиома дает критерий, корректно отражающий правило «чем больше, тем лучше» и неприятие риска.

Историческая справка

В 1738 г. была опубликована статья Даниила Бернулли (D. Bernoulli), швейцарского математика, работавшего в Петербурге, посвященная разрешению так называемого петербургского парадокса.

Рассматривается игра с начальной ставкой 1 руб. Бросается правильная монета (т.е. такая монета, для которой выпадение решетки или герба равновероятно). В случае выпадения герба игрок получает выигрыш, равный ставке, в случае выпадения решетки ставка удваивается. Игра ведется до выигрыша.

Напомним, что математическим ожиданием дискретной случайной величины^[1] имеющей распределение р_х = Р{Х = х}, i = 1, п_} называется величина.

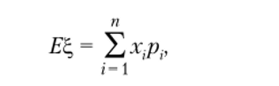
если число значений случайной величины конечно. Если число значений случайной величины счетно, то.

При этом, если ряд в правой части равенства расходится, то говорят, что случайная величина не имеет математического ожидания.

Таким образом, ожидаемый выигрыш бесконечен.

Во времена Бернулли математическое ожидание было общепринятой мерой оценки случайных денежных альтернатив. Поэтому следующий факт, обнаруженный Бернулли, выглядел парадоксально. Оказалось, что большинство людей, кроме очень богатых, были готовы продать право сыграть в такую игру за вполне умеренные суммы. Именно это несоответствие результата эксперимента принятой тогда теории и получило название «петербургского парадокса».

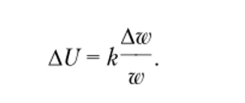
Вычислим математическое ожидание выигрыша в данной игре.

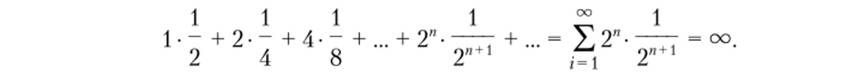
Для разрешения парадокса Бернулли ввел функцию (фактически функцию полезности денежного выигрыша) U (w), выражающую субъективную ценность богатства w (измеряемого в денежных единицах). Бернулли ввел также принцип уменьшения полезности денег в зависимости от уже имеющегося богатства. Проиллюстрируем этот принцип следующим примером. Человек, имеющий 10 000 долл., будет рад получить еще 10 000 долл.; но если у индивидуума есть 1 000 000 долл., то получение 10 000 долл, уже не будет иметь для него такого большого значения и, следовательно, не так сильно увеличит его полезность. Бернулли сделал конкретное предположение о том, что полезность прирастает пропорционально относительному, а не абсолютному приращению капитала, Таким образом, приращение капитала в 10 000 долл, для индивидуума, имеющего капитал 1 000 000 долл., составит kX 1% приращения полезности, что должно быть равнозначно приращению в 100 долл, для имеющего 10 000 долл. При пере;

dw

ходе к бесконечно малым приращениям получим dU = к—, откуда очевидным.

w

образом получаем U (w) = k (w) + b, где k, b — некоторые постоянные коэффициенты, k > 0. Таким образом, функция полезности Бернулли имеет логарифмический вид.

Далее Бернулли предложил вместо математического ожидания самой величины X использовать для ее оценки математическое ожидание ее полезности EU (x). Таким образом, введенное Бернулли понятие полезности разрешило петербургский парадокс, установив одновременно нелинейный характер самой полезности. Другим ученым, предложившим аналогичное правило решения петербургского парадокса, был немецкий математик Г. Крамер, сделавший это даже на несколько лет раньше. Он использовал функцию полезности вида U (x) = л[х.

Таким образом, анализ рисковых альтернатив дал первый толчок возникновению теории полезности, впоследствии занявшей столь видное место в экономической теории. Анализу рисков посвящен материал гл. 15. Здесь займемся изучением теории полезности.

• [1] Севастьянов Б. Л. Kvpc теории вероятностей и математической статистики. М.: Наука, 1982. 256 с.