Сравнительный анализ методов расчета VaR

Поскольку современный финансовый риск-менеджмент оперирует показателями на основе value at risk, необходимо четко представлять себе, какой из методов расчета VaR и в каких условиях показывает наилучшие результаты.

Параметрический метод построения VaR прост в использовании, допускает аналитическое представление, не требует полной переоценки позиций, не требует обширной базы ретроспективных данных, однако имеет ряд минусов, главным из которых является то, что гипотеза о нормальном распределении, как правило, не соответствует параметрам реального финансового рынка. Данный метод также плохо подходит для оценки риска активов с нелинейными ценовыми характеристиками.

Метод исторического моделирования, относящийся к методам полного оценивания, позволяет наглядно и полно оценить риск с учетом «толстых хвостов» без предположений о характере распределения, однако он предполагает наличие обширной базы данных по всем факторам риска.

Метод стохастическою моделирования (метод Монте-Карло) считается наилучшим, так как обладает рядом достоинств, в частности, нс использует гипотезу о нормальном распределении доходов (убытков), показывает высокую точность для нелинейных инструментов и устойчив к выбору ретроспективы. К недостаткам метода можно отнести техническую сложность расчетов и модельный риск.

Еще одной мерой риска может являться специальная характеристика, которая оценивает отклонение значений случайной величины ^ влево и вправо от своего математического ожидания Е (?,). Для удобства можно рассмативать две вспомогательные числовые характеристики:

• среднее левое (нижнее) отклонение

• среднее правое (верхнее) отклонение

Если случайная величина ^ характеризует случайный доход, то числовая характеристика К является мерой риска и говорит о том, что при достаточно большом количестве реализаций случайной величины ^ усредненный недобор ее значений до т, будет примерно равен К. Полагаем при этом, что т, = ?(?,) — это значение математического ожидания случайной величины 2,^[1].

При этом характеристика К имеет обратный смысл: при достаточно большом количестве реализаций ?, усредненный перебор ее значений сверх т, будет примерно равен К. Если случайная величина характеризует случайный убыток, то, наоборот, мерой риска служит К.

Эти числовые характеристики обладают важным для приложений свойством: их значения всегда равны между собой не только для распределений, симметричных относительно математического ожидания, но и для асимметричных распределений. Поэтому можно ввести единую характеристику /г, = h_t = h^y которую будем называть средним полу отклонением. Введенная характеристика обладает следующим свойством.

Среднее полуотклонение равно среднему левому и среднему правому отклонениям: К — К — К.

S S S.

Доказательство справедливости равенства К ⁼ К проводится непосредственно на основании определений соответствующих числовых характеристик. В силу симметрии при замене ?, на величина среднего полуотклонения остается неизменной.

Поскольку среднее полуотклонение тесно связано с математическим ожиданием, то при анализе задач принятия решений в условиях вероятностной неопределенности использовать эти характеристики следует совместно (при необходимости можно также вычислить еще и подходящую пороговую характеристику). Среднее полуотклонение не только является интерпретируемой характеристикой, но и обладает целым рядом свойств, важных для приложений. Поэтому его возможно применять, например, вместо среднего квадратического отклонения.

Свойства среднего полуотклонения — пусть случайная величина г получается из % афинным преобразованием: г = + Ь. Тогда значение дисперсии D® вычисляется с помощью значения дисперсии Z)(^), поскольку среднее полуотклонение обладает свойством однородности по модулю.

Свойство (однородность по модулю) — если выполняется соотношение ^то h_n = kh;.

Справедливость этого свойства можно проверить при помощи использования свойств математического ожидания. Таким же свойством обладает и среднеквадратичное отклонение а, но не дисперсия D (^) или VaR_y(%). Из (15.15) следует, что полуотклонение обладает также следующими двумя свойствами, которые считаются важными для мер риска.

|| Если г| = k%_y k > 0, то h = kh*.

Свойство положительной однородности гарантирует сохранение масштаба, т. е. при переходе к другим единицам измерения дохода % (например, от рублей к долларам) величина среднего отклонения также будет исчисляться в новых единицах. Этим свойством обладает также VaR_y(%).

|| Если г| =? + Ь, то = К.

Благодаря свойству (инвариантность к сдвигу), например, среднее отклонение для гаммараспределения со сдвигом такое же, как для гамма-распределения^[2].

Условия несклонности к риску или неприятия риска также можно применить к среднему полуотклонению. Поскольку для меры риска, связанной с математическим ожиданием, должно выполняться требование того, что ее значение для случайной величины rj было больше (или хотя бы не меньше), чем для случайной величины ?, данному требованию удовлетворяют дисперсия и среднее квадратическое отклонение. Из определения среднего полуотклонения можно сделать вывод, что эта мера риска также удовлетворяет этому требованию.

Свойство (монотонность относительно растяжения) — если функция распределения G случайной величины ц получена из функции распределения Fслучайной величины? растяжением с сохранением среднего, то /?_л > /г,.

Целесообразность диверсификации риска, в основе которой лежит идея компенсация риска одних вложений за счет других, выражают в виде требования субаддитивности мер риска (если ?, — случайные убытки). Среднее полуотклонение обладает таким свойством.

Свойство (субаддитивность) — || Если случайная величина равна р =? + ц, то < К + к_ц.

Доказательство проводится с использованием свойств математического ожидания и опирается на неравенство.

Свойством субаддитивности для произвольных распределений обладает также среднеквадратическое отклонение а,. Мера риска VaR_v(^) обладает этим свойством только в случае нормального распределения случайной величины^[3], дисперсия D (t>) не обладает этим свойством (однако она аддитивна для независимых случайных величин).

В общем случае можно оценить величину отношения величин К и а,.

Свойство н — если случайная величина не является постоянной, то для L = — справедлива.

^а4.

интервальная оценка, которую нельзя улучшить

Здесь pi есть вероятность того, что значение случайной величины ?, будет равно се математическому ожиданию: pi = Р{?, = т,. Для непрерывной случайной величины зга вероятность равна нулю. Таким образом, согласно.

(15.16), среднее нолуотклонение всегда в два или более раз меньше, чем среднее квадратическое отклонение (если оно отлично от нуля).

Справедливость оценки сверху устанавливается для дискретных и непрерывных случайных величин при помощи неравенств Коши и Коши — Буняковского^[4][2] соответственно; нижняя оценка очевидна. То, что оценка.

(15.16) является неулучшаемой, показывают следующие примеры. Для случайной величины |, принимающей значение 0 с вероятностью р е [0; 1) и значения -1 и 1 с равными вероятностями (1 — р)/2, отношение.

W1^/2. с другой стороны, для любого сколь угодно малого числа е > 0 существует такое положительное число а, при котором для логнормального распределения t. = е (см. табл. 15.3).

Соотношение среднего полуотклонения и односторонних средних квадратических отклонений можно представить также неравенством с использованием вероятностей /С = Р[?, < т_;] и pt = Р[?, > т,|.

Справедливо неравенство.

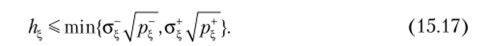
Эта оценка является неулучшаемой, так как, например, для случайной величины введенной при анализе предыдущего свойства, указанное нестрогое неравенство обращается в равенство. Согласно (15.17), среднее полуотклонение всегда меньше любого из односторонних среднеквадратических отклонений (если они не обращаются в нуль).

Односторонними аналогами неравенства Чебышева^[4] для среднего квадратического отклонения являются два неравенства для односторонних средних квадратических отклонений, доказываемые подобным же образом (в них, А > 0)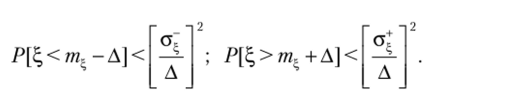

Среднее нолуотклонение обладает сходным свойством.

Справедливы неравенства (для любого, А > 0):

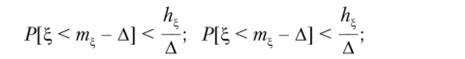
Вычисление среднего полуотклонения /ц можно согласно общей формуле Для дискретных распределений вычисления упрощаются, поскольку все сводится к вычислению конечных сумм. Например, для распределения Пуассона с параметром X > 0 (напомним, что математическое ожидание т_ь = X)

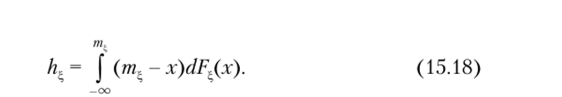
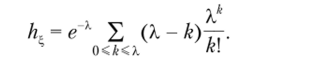
Для непрерывных распределений справедлива формула.

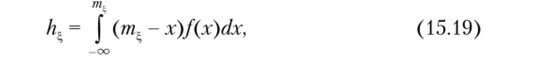
где f (x) — функция плотности распределения вероятностей.

Используя (15.19), можно получить формулы для вычисления h, и L для основных непрерывных распределений. Некоторые из них приведены в табл. 15.4.

Таблица 15.4

Формулы для вычисления h^ и ^ для основных распределений.

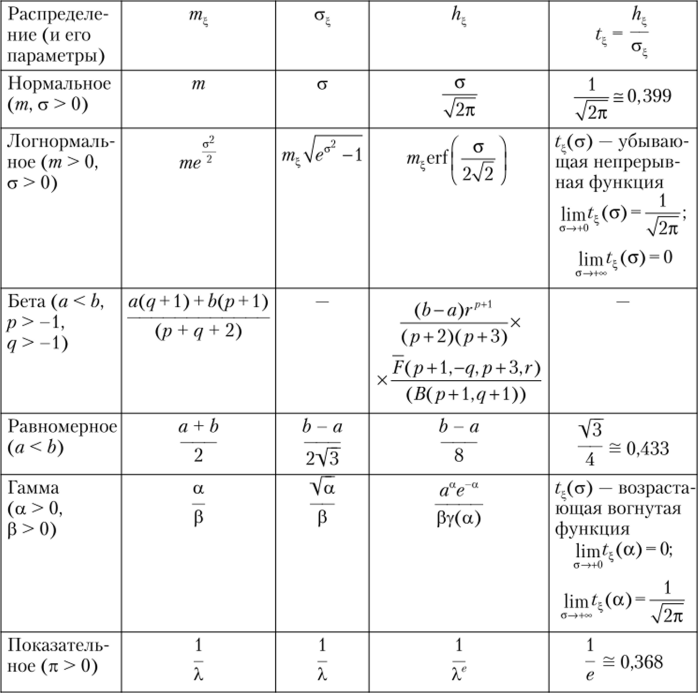
2 ^г з Здесь cri (z) = —j= e~^r dt — интеграл вероятности; F — гипергеометриче- yjn^j₀

ская функция Гаусса; р, у — бетаи гамма-функции. Для бета-распределения r=(p+ 1 )/{р + q + 2)¹.

Мера риска VaR как статистика, характеризующая риск инвестиционного портфеля, обладает многими достоинствами, главными из которых являются относительная простота представления информации о риске (в виде только одного значения в стоимостном выражении) и практическая полезность для управления портфелем. Однако поскольку VaR представляет собой только одну заданную квантиль распределения прибылей и убытков, он имеет и целый ряд существенных недостатков, в том числе следующие.

• • Отсутствует информация о наихудшем возможном убытке за пределами значения VaR. Например, при заданном уровне доверия (1 — у) = 0,95 остается неизвестным, какими могут быть потери в оставшихся 5%. Иначе можно сказать, что метод VaR, являясь квантильной оценкой, фактически оперирует лишь с одной точкой функции распределения — той, где функция распределения пересекает уровень 1 — у. Поэтому, например, расчет Var_y(%) может быть очень чувствителен к выбору у.
• • Отсутствует информация о виде распределения убытков: у распределений с разной толщиной «хвостов» при определенном уровне доверия может наблюдаться одно и то же значение VaR.
• • Мера VaR не является однозначно определенной: для одного и того же портфеля уровни доверия его значения могут существенно различаться — в зависимости от способа декомпозиции портфеля по факторам риска, объема выборки исторических данных и применяемого метода расчета. Поэтому можно делать выводы только о статистической точности модели расчета VaR, оцененной, но большим выборкам данных.

Как было отмечено ранее, при применении VaR необходимо оценить, можно ли пренебречь хвостами распределения. На рис. 15.5 представлены две гистограммы доходов (убытков).

Видно, что несмотря на то, что VaR одинакова, для одной из гистограмм маловероятные значения больших убытков могут оказаться значимыми, и их необходимо принимать во внимание. О таких распределениях говорят, что они имеют тяжелый хвост.

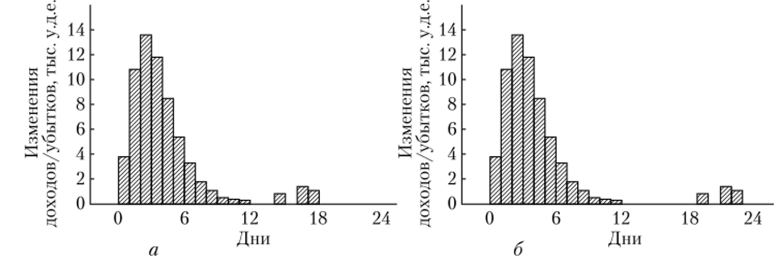
Рис. 15.5. Гистограммы выборок с одинаковыми VaR уровня у = 2,5%.

¹ Подиновский В. В. Указ, соч.; Бронштейн И. II., Семендяев К. А. Указ. соч.

В связи с этим целесообразно дополнить вычисление VaR какими-либо характеристиками хвостов. Например, можно вычислить математическое ожидание при условии превышения убытком некоторого уровня.

где ?, — случайная величина убытка; k — некоторое число.

Усовершенствованные меры риска хвоста можно построить на основе (15.20), делая k зависимым от Например, предлагалась мера.

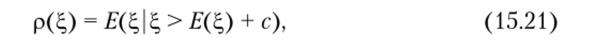
где с — фиксированное число, которое не зависит от распределения Е (?) — математическое ожидание Можно заметить, что эти меры риска не удовлетворяют условию однородности. Чтобы получить меру риска, удовлетворяющую этому условию, нужно взять в качестве р в (15.20) некоторую меру риска, которая сама по себе удовлетворяет этому свойству. Например, можно взять k = Е(?) + аа,.

Одна мера риска такого типа — условное математическое ожидание хвоста (tail conditional expectation — ТСЕ)^[7]:

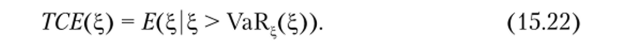
Исходя из приведенных выше рассуждений возникает вопрос, насколько целесообразно использовать квантили распределений прибылей и убытков в качестве меры риска. В качестве альтернативы можно было бы рассмотреть такие используемые в финансовой сфере меры риска, как:

• • полное распределение прибылей и убытков по портфелю, для которого можно определить уже набор квантилей разных порядков;
• • дисперсия {стандартное отклонение) доходности, которая учитывает большие по величине колебания цен. В то же время большая дисперсия доходности может объясняться как значительными по величине убытками, так и прибылями;
• • полудисперсия доходности, отличающаяся от обычной дисперсии тем, что отражает разброс только тех значений, которые меньше среднего

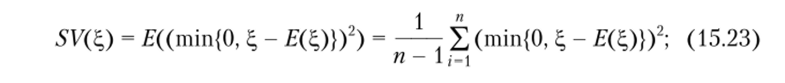
• нижний частный момент порядка п

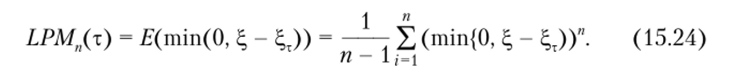
Для случая п = 2х_Т = Е (^_Т) нижний частный момент будет равен полудисперсии;

• абсолютное отклонение, представляющее собой математическое ожидание абсолютных значений отклонений от среднего:

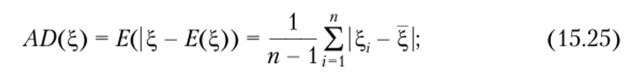
• модифицированный коэффициент Джини:

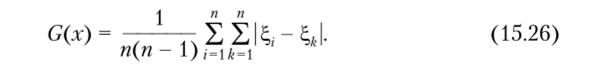
Все перечисленные меры риска обладают различными достоинствами и недостатками, однако не все эти меры обладают «идеальными» свойствами, необходимыми для решения задач финансового риск менеджмента. Такие идеальные свойства были сформулированы в работе Ф. Артзнера и др. «Coherent measures of risk»^[8].

• [1] Подиновский В. В. Указ. соч.
• [2] Феллер В. Указ. соч.
• [3] Шоломицкий А. Г. Указ, соч.; Энциклопедия финансового риск-менеджмента / под ред.А. А. Лобанова и А. В. Чугунова.
• [4] Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. 13-е изд., испр. М.: Наука, 1986. 544 с.
• [5] Феллер В. Указ. соч.
• [6] Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. 13-е изд., испр. М.: Наука, 1986. 544 с.
• [7] Шоломицкий А. Г. Указ. соч.
• [8] Artzner Ph., Delbaen F., EberJ.-M., Heath D. Coherent measures of risk // MathematicalFinance. 1999. P. 203—228; Кустицкая T. Л. Аксиоматика обобщенных когерентных мер риска. XIV Международная конференция, но эвентологической математике и смежным вопросам. Красноярск, 2010; Энциклопедия финансового риск-менеджмента / под ред. А. А. Лобанова и А. В. Чугунова.