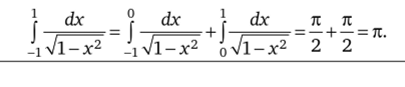Несобственный интеграл 2-го рода

Рассмотрим теперь функцию /, определенную на конечном промежутке [а, Ь] (за исключением, быть может, концов этого отрезка), но неограниченную на нем. Предположим, ради определенности, что на любом отрезке вида [а, b — е] (0 < е < b — а) функция ограничена и собственно интегрируема, но является неограниченной в левой окрестности точки Ъ. Точка b в этом случае, вне зависимости от того, определена функция в этой точке или нет, носит название особой точки (2-го рода).

b-t

Предел интеграла J f{x)dx (конечный или бесконечный) при? ->+0.

а

называют несобственным интегралом 2-го рода от функции/от а до b и обозначают символом.

В случае, когда этот предел конечен, говорят, что интеграл (4.3) сходится, а неограниченную функцию/называют интегрируемой в пределах от а до b (в несобственном смысле). Если же предел (4.3) бесконечен или не существует, то про интеграл говорят, что он расходится, а функция/— неинтегрируема на данном промежутке. В частности, если этот предел равен +°°, то говорят, что интеграл расходится к +°°. ь ь

Аналогично f f (x)dx = lim f fWdx в случае, если а — особая точка.

а

Так же как и в случае с собственным интегралом, по определению будем считать, что если функция/интегрируема на промежутке [а, Ь], то.

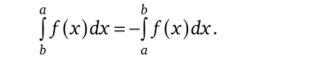
В общем случае на промежутке [а, Ъ] может быть конечное число особых точек с₁, с₂,…, с_т, вблизи которых функция/неограничена, в то время как на любом отрезке, принадлежащем [а, Ь] и не содержащем особых точек, функция ограничена и интегрируема. Пусть, например, таких особых точек три, причем две из них совпадают с концами а, b промежутка, а третья, с, лежит между ними. Тогда интеграл от/в пределах от а до b определяется следующим образом:

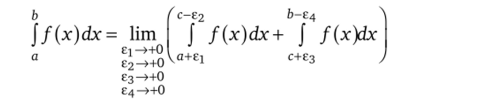
при одновременном, но независимом стремлении к нулю положительных чисел е_х, в₂, ?3, ?4.

Для несобственных интегралов на бесконечном промежутке особых точек может быть бесконечно много, лишь бы в каждом конечном промежутке [а, А] их было бы конечное число.

При исследовании несобственных интегралов на сходимость (как и при вычислении их по определению) выясняют сходимость интеграла в окрестности каждой из особых точек (если особая точка 2-го рода, то отдельно в левой и правой ее окрестностях). Интеграл считается сходящимся, только если он сходится в каждой окрестности каждой своей особой точки. В противном случае интеграл считают расходящимся.

Замечание 4.2. С помощью подстановки t = ^ рассмотренный.

Ъ-х

выше несобственный интеграл 2-го рода с особенностью в точке Ъ приводится к несобственному интегралу 1-го рода (при этом особенность 2-го рода преобразуется в результате указанной подстановки в особенность 1-го рода).

^ dx

Пусть, например, дан несобственный интеграл J- (а<�Ъ),.

а{Ь-х)^р

где подынтегральная функция неограничена в левой окрестности точки Ъ.

_ 1, 1 , dt

Сделав подстановку t--, получим x = b—, ах = — и, следова;

b-x t t¹

тельно,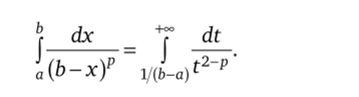

Пользуясь определением, исследовать сходимость несобственных интегралов: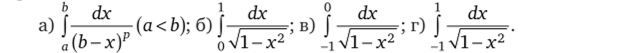

Решение, а) Функция —-— ограничена и интегрируема на любом про- (Ъ-х)^р

межутке [а, Ь-е] (0<�е0, при х->Ь-0 ее значение неограниченно возрастает (точка х = b является особой). При р ф 1 по определению находим.

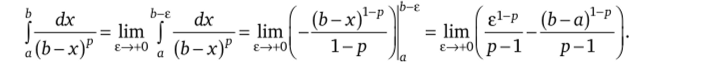
gi-p.

Если р < 1, то lim-= 0 и, следовательно, интеграл сходится (к своему.

• ?—"+о р — 1
• (Ь-а)¹~^р е'-г

значению ⁱ——). Если р>1, то Иш-= +<�", а значит, интеграл расхо;

1 — р е->+о р -1.

дится (к-н>о).

При р = 1 имеем.

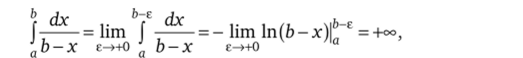
т. е. интеграл расходится.

Итак, при р 1 — расходится.

б) Функция, ограничена и интегрируема на любом отрезке [0,1 — е],.

v 1-х²

где 0 < е < 1, и в точке х = 1 (единственная особая точка на промежутке интегрирования) значение функции обращается в бесконечность. По определению,.

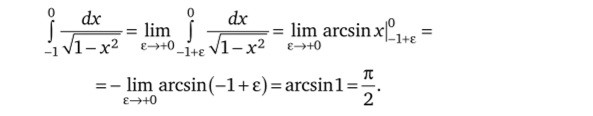aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">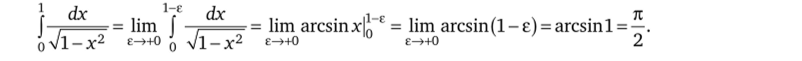

• в) Особая точка х = -1:
• г) Имеем две особые точки х = ±1: