Метод Кона — Шэма

В связи с тем что функционал кинетической энергии от плотности неизвестен, а через волновую функцию кинетическая энергия вычисляется легко, существует оригинальный метод Копа — Шэма, совмещающий подходы на основе волновой функции и электронной плотности. В данном методе функционал электронной энергии содержит несколько частей.

В приведенном выражении 7″ ₍₎[р] — функционал кинетической энергии электронов в совпадающей с рассматриваемой по строению и распределению электронной плотности р молекулярной системе, но в которой пренебрегаются электрон-электронные взаимодействия. Это предположение часто называется приближением невзаимодействующих электронов. Функционал Е[р] характеризует энергию притяжения электронов к ядрам; [/[р] отвечает за кулоновское взаимодействие электронов, которое одновременно включает и искусственное взаимодействие электрона с самим собой; Е [р] — функционал обменно-корреляционной энергии, включающий все остальные вклады в энергию, которые не учитываются предыдущими слагаемыми. В частности, он включает: энергию обменного взаимодействия электронов; электронную корреляцию; часть кинетической энергии, на которую необходимо скорректировать 7'_(|[р|, чтобы получить кинетическую энергию реальной системы; поправку на самовзаимодействие электрона в выражении для кулоновского потенциала. На самом деле функционал Е Др] включает все скрытые дефекты данного метода.

Вводя вспомогательные одноэлектронные функции (орбитали Кона — Шэма — (р^ю) и применяя вариационный принцип, получают одноэлектронные уравнения, по форме совпадающие с уравнениями метода Хартри — Фока.

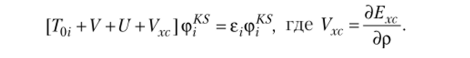
Однако данные уравнения гораздо проще, чем соответствующие уравнения метода Хартри — Фока, в котором оператор Фока содержит члены потенциальной энергии V. и G., зависящие от индексов электронов, и является нелокальным. В данном же выражении суммарный функционал потенциальной энергии V_efJ. зависит только от места расположения в пространстве выбранной точки и является одним и тем же для всех электронов. Орбитали Кона — Шэма, получающиеся решением последнего уравнения, могут быть непосредственно использованы для нахождения общей электронной плотности.

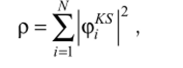
которую можно использовать для расчета улучшенного значения V_efj, приводящего к новому циклу самосогласованного ноля. Орбитальные энергии определяются соотношением.

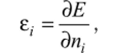
где п. — заселенность орбитали, которая может изменяться в интервале 0—1.

Полученное значение электронной плотности используется для расчета общей энергии по уравнению (11.2), в котором кинетическая энергия рассчитывается с помощью соответствующих орбиталей Кона — Шэма, а не через плотность.

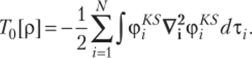
Следует подчеркнуть, что все орбитали Копа — Шэма и их энергии не имеют строгого физического смысла. Главная их роль заключается в установлении связи между кинетической энергией и электронной плотностью. Следует отметить, что отрицательное значение энергии высшей занятой орбитали соответствует первой энергии ионизации системы. В то же время и остальные орбитали и их энергии имеют большое полуколичественное значение. Появляются все новые сведения о возможности физической интерпретации подобно орбиталям Хартри — Фока и более глубоко расположенных занятых, а также незанятых орбиталей Кона — Шэма. В отличие от МО Хартри — Фока молекулярные орбитали Кона — Шэма учитывают корреляционные эффекты.

Практически электронная энергия рассчитывается через орбитальные энергии.

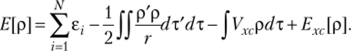
Для практического использования метода DFT необходимо иметь представление о величине ?_г|р]. Простейшее описание данной величины осуществляется с помощью приближения локальной плотности (Local Density Approximation — LDA). В данном подходе обменно-корреляционная энергия определяется простым выражением.

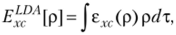
где е_гг — обменно-корреляционная энергия, приходящаяся на один электрон, в однородно взаимодействующем электронном газе с плотностью р. Аналитический вид данной функции неизвестен, но она последовательно улучшается на основе имитации методом Монте-Карло и описывается аналитическим выражением. Локальные функционалы, полученные для электронного газа, приводят к недооценке обменной энергии (-15%) и переоценке корреляционной энергии (иногда на 100%). Однако по абсолютной величине ошибка расчета обменной энергии больше, чем корреляционной энергии. Приближение LDA переоценивает прочность обычных химических связей и недооценивает прочность водородных связей. Орбитали Кона — Шэма в приближении LDA обычно нс сильно отличаются от орбиталей Хартри — Фока.

Для удобства обменно-корреляционную энергию разбивают на две части — обменную? [р| и корреляционную? [р] энергии.

Предшественником современного метода DFT является Ха-метод, разработанный Слэтером. В этом методе обменная энергия аппроксимировалась выражением.

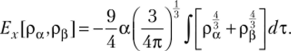
Здесь обменная энергия является функционалом электронной плотности со спином+½(р_а) и—1 /2(р_р) и содержит подгоночный параметр а. Эмпирически оптимальные значения этого параметра для большинства атомов элементов периодической системы находятся в пределах от 0,7 до 0,8. Для специального случая — однородного электронного газа.

^а=з'.

Были малоуспешные попытки улучшить функционалы с помощью градиентного приближения (Gradient Expansion Approximation — GEA), в котором? Др] представляется в виде ряда Тейлора относительно р и который обрезается на его линейном члене.

Существенного улучшения результатов удалось добиться при другом подходе, использующем приближение обобщенных градиентов {General Gradient Approximation — GGA). Разложение ?.Др] в этом случае является нелинейным и учитывает его асимптотический характер. Такие расширенные функционалы часто называются нелокальными или градиентными поправками, так как они зависят не только от плотности, но и также от величины градиента (т.е. первой производной V) плотности в данной точке.

Таким образом, имеем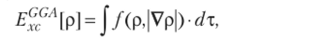

где / — функция двух переменных. Современные нелокальные функционалы имеют весьма сложный вид, в котором значение плотности и ее градиент являются неотъемлемыми частями формулы.