Алгоритм выбора размера шага в процедуре интегрирования по методу дифференциальной гомотопии

Для выбора размера шага интегрирования использовался известный алгоритм, который основывается на элементарных асимптотических оценках.

Пусть первые два шага процедуры по методу Ньютона приводят к коррекции у в z¹ и из г в г² (рис. 6.13). Пусть также dy = |у — z¹1| и d₂ = ||z² — z' || (где d, di — длина 1 -го и 2;

го шага коррекции Ньютона соответственно; z z — результаты 1 -ой и 2-ой коррекции Ньютона соответственно), тогда отношение а = — согласно теореме Ньютона-Канторовича ^d

будет не больше^, если у находится в области квадратичной сходимости метода Ньютона. Обозначим в угол между последующими единичными тангенсами, как показано на рис. 6.13, т. е. в = arc cos[(m* J z/⁺ⁱ .

Известно, что для метода интегрирования по формуле Эйлера.

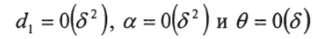
где 5- размер шага: S=As; 0 — порядок в асимптотических оценках.

Если а = о ( 2), тогдаДстремится к константе, как 5

о

стремится к нулю.

Алгоритм выбора размера шага (/?) основан на сравнении экспериментальных значений трех параметров:

• — dj — идеальной длины для первой коррекции Ньютона dx
• -а, - идеального отношения сжатия;
• — в у — идеального угла между двумя единичными тангенциальными векторами в алгоритме Джорджа.

Мультипликативный фактор /? размера шага в алгоритме Джорджа получен из соотношения размеров шагов: 8^к+| = рб^к. Значение величины 6^к" выбирают таким образом, чтобы получить идеальное соотношение сжатия а" а константу С так, чтобыа = С8^г, в особенности а, = CS², .

Членами более высокого порядка в 8 пренебрегаем, тогда v ‘а,.

= ^Зиьы = Р8; поэтому.

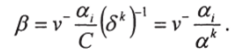
Аналогично можно получить (d,)*⁺¹ = d, используя выражение.

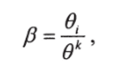
и для в = в,

где в — угол вращения на к-м шаге гомотопии.

Обобщенный алгоритм выбора размера шага, если принять р = mini v'—, v' —, —, имеет следующий вид.

d, а в)

1. Ввод данных:

*° - начальное приближение;

<5° - начальный размер шага;

di — идеальная длина для первой коррекции Ньютона; а(- идеальное отношение сжатия; в, — идеальный угол вращения; е — требуемый допуск для ||/||.

• 2. Присвоить х = х°, к = 0, <5 = Х= 1
• 3. Принять к: = к +1
• 4. Вычислить и, единичный тангенциальный вектор;
• 5. Выполнить логические операции:

Если к > 1, то в = arc cosli/"¹^ w*], р = min (/?,#,/#); Если P < ½, то 5: = S/2,k := к -1, идти на пункт 7;

• 6. Если к >, то 5: = PS.
• (x
• 7. Вычислить у = у — + ди только в том случае, если 6 не

Ы делится пополам так много раз, что начинает работать процедура «Ошибка».

8. Рассчитать (дх⁷, ДЛ)^? — длину первой коррекции Ньютона.

^ d ^ 1 S.

9. Вычислить у при Р = тт 2, v~—; если Р<~, 6:= — ,

К ^d) ^{2 2}

идти на шаг 7.

10. Рассчитать (дх⁷, ДЛ)^Г — длину второй коррекции Ньютона, отношение сжатия в алгоритме Джорджа.

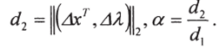
11. Вычислить у при р = minf 2, v' — |, если Р <�—, 5:= — ,

V а) 2 2.

идти на шаг 7.

12. Проверить Я < 0? Если нет, то идти на шаг 3 при условии, что максимальное число шагов не превышено (в этом случае начинает работу процедура «Ошибка»), Если да, начинается последняя процедура коррекции Ньютона в гиперплоскости Л=0.

При обращении к процедуре «Ошибка» (например, как в случаях, показанных на рис. 6.14) определяется причина ошибки и пересчитываются параметры d_it, а, или в,.

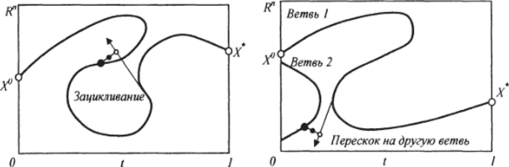
Рис. 6.14. Процедура «Ошибка».

Если отказаться от расчета отношения сжатия а, то одной коррекции Ньютона достаточно для подбора величины шага и, следовательно, количество расчетов может быть уменьшено на треть.

Как показали исследования, применение дифференциальной гомотопии Ньютона к решению проблем моделирования каскада взаимосвязанных колонн очень часто приводит на промежуточных шагах к абсурдным с физической точки зрения решениям (отрицательным величинам и т. п.), поскольку математическое описание системы разделения в значительной мере зависит от физико-химических свойств разделяемой смеси. Применение ограничений не всегда дает положительный эффект и иногда сильно затрудняет процесс поиска корней системы.

Поэтому желательно выбирать траектории гомотопии, лежащие в области реальных физических величин. Например, использовать термодинамические функции гомотопии при определении константы парожидкостного равновесия Кц.

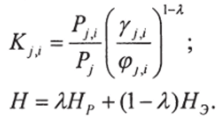
где Pj, i, Pj — парциальное давление /-го компонента, давление на у-й ступени контакта соответственно; ~ коэффициент активности /-го компонента, коэффициент фугитивности /-го компонента на у'-й ступени контакта соответственно; Я — линейный параметр гомотопии; Н_э — расчетное, экспериментальное значение функции гомотопии соответственно.

Несмотря на то, что применение термодинамической функции гомотопии, значительно увеличивает область сходимости по сравнению с методом Ньютона, для увеличения надежности алгоритмов при моделировании сложной системы взаимосвязанных колонн разделения, теплообменников и клапанов наилучшим будет применение комбинации функций термодинамической и дифференциальной гомотопии.

Поэтому был разработан обобщенный алгоритм моделирования и оптимизации сложных взаимосвязанных систем разделения с использованием методов гомотопии, заключающийся в следующем.

1. Записать математическое описание системы разделения:

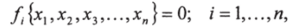
где п- число неизвестных.

2. Составить функцию термодинамической гомотопии с линейным параметром Л₀:

где п; Д7 <�Л, <�Л7;*, = *Г" приХ^Н_а =/приЛ7;

3. Составить функцию дифференциальной гомотопии с линейным параметром Я:

где п- ЯГ" <�Л <�ХГ;у, = *, приЯ," «;^ = Я₀₍приДГ^ж

4. Преобразовать систему нелинейных алгебраических уравнений в систему обыкновенных дифференциальных уравнений с переменной длиной траектории гомотопии Р (принимая y"₊i =Л;у_л+2=Л)^:

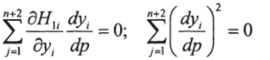
5. Рассчитать матрицу частных производных.

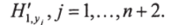
6. Проинтегрировать систему дифференциальных уравнений шага 4 любым численным методом (например методом Эйлера) для выбранного Ар:

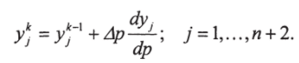
7. Произвести коррекцию у_р полученных методом Ньютона или его модификацией решением системы шага 3, с полученными значениями уу^(А) в качестве начального приближения:

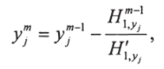
где — матрица частных производных на (т-1)-м шаге.

8. Проверить условия окончания расчетов (переход на шаг 5 или 3).

Разработанные обобщенные алгоритмы моделирования и оптимизации систем разделения с использованием методов гомотопии вошли в состав системы автоматизированного расчета химико-технологических процессов.