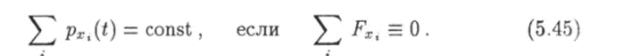Уравнение изменения импульса системы частиц

Рассмотрим систему, состоящую из N материальных точек. Каждой из этих точек припишем некоторый порядковый номер i = 1, 2, …, N. Пусть г, есть радиус-вектор частицы с номером i. Этот вектор определяет положение частицы относительно некоторой инерциальной системы отсчета. Движение всех частиц системы можно описать при помощи N векторных функций.

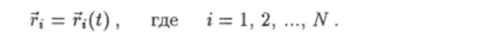
Каждая из этих функций подчиняется второму закону Ньютона. Запишем уравнения движения частиц. Для этого классифицируем действующие на них силы.

Каждая частица системы в общем случае взаимодействует не только с другими частицами этой системы, но также она может испытывать воздействие со стороны частиц, не входящих в состав исследуемой системы. Сила fit, с которой частица под номером к действует на частицу под номером t, называется внутренней, если обе частицы принадлежат данной системе. Сила F, характеризующая воздействие, которое оказывают на i-ю частицу частицы, не принадлежащие данной системе, называется внешней. Учитывая все силы, действующие на частицу под номером i, запишем второй закон Ньютона для этой частицы:

где т, — масса i-й частицы, i = 1, 2, …, N суммирование внутренних сил fik производится по всем значениям индекса к, кроме к = i. Соответствующие различным значениям индекса i уравнения (5.38) вместе взятые образуют систему для неизвестных функций г, = г,-(<). Однако следует заметить, что уже для трех взаимодействующих частиц решение этой системы в общем случае представляет собой очень сложную математическую задачу.

Импульсом системы материальных точек называют сумму импульсов всех частиц этой системы:

где.

— импульс г-й частицы.

Предполагая, что число частиц в системе со временем не изменяется, продифференцируем равенство (5.39) по времени:

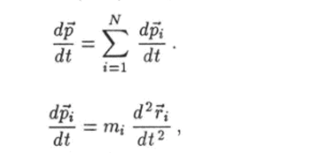
Так как с учетом уравнений движения (5.38) получим:

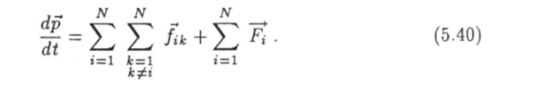
Первая сумма в правой части этого равенства, т. е. сумма всех внутренних сил, содержит как силу /"•*, с которой k-я частица действует на г-ю частицу, так и силу /*,*, с которой i-я частица действует на частицу под номером к. Таким образом, все слагаемые в этой сумме можно разбить на пары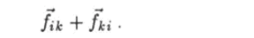

В силу третьего закона Ньютона это выражение равно нулю. Поэтому сумма всех внутренних сил также равна нулю: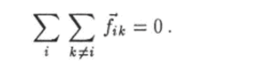

При этом уравнение (5.40) принимает вид.

Согласно этому уравнению производная по времени от импульса системы материальных точек равна сумме всех внешних сил, действующих

на систему.

Из уравнения (5.41) вытекает закон сохранения импульса, который формулируется следующим образом. Импульс системы материальных точек не изменяется со временем, если сумма всех внешних сил, действующих па систему, тождественно равна нулю. В самом деле, если.

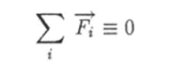
на некотором отрезке времени, то р = 0, т. е. импульс системы в течение этого времени остается постоянным:

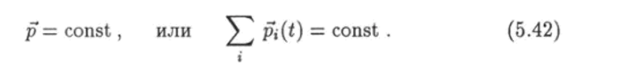
Однако импульсы отдельных частиц могут изменяться вследствие их взаимодействия друг с другом или под действием внешних сил.

Из равенств (5.42) следует, что импульс системы частиц в некоторый момент времени t равен импульсу этих частиц в любой другой момент времени *2^:

или где левые и правые части равенств соответствуют различным моментам времени.

Согласно уравнению (5.41) проекция р_х на ось х вектора импульса системы частиц изменяется со временм так, что ее производная равна сумме проекций на эту ось всех внешних сил:

Из уравнения (5.44) следует, что в том случае, когда сумма проекций всех внешних сил на некоторое направление равна нулю, проекция импульса системы на это направление не изменяется со временем: