Задачи к разделам I и II

Раздел I Задачи к главе 1.

Задача 1. Найти изменение объема воды в емкости при нагреве ее от 20 до 40 °C. Объем воды V= 100 м³. Коэффициент объемного расширения в интервале температур 20—40°С при давлении 10° Па p_v = 0,29 1/К.

Решение. Коэффициент объемного расширения капельных жидкостей, определяющий изменение их объема при увеличении температуры, находится по формуле: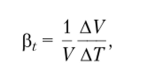

где V— первоначальный объем жидкости; А К— изменение объема при увеличении температуры на величину АТ.

Из формулы для р, получаем: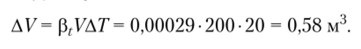

Задача 2. Найти плотность воды при возрастании ее температуры от 20 до 40 °C.

Решение. Плотность находится по формуле:

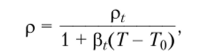
где р, = 998 кг/м³— плотность при температуре 20 °C; р, = 0,29 — коэффициент температурного расширения.

Отсюда: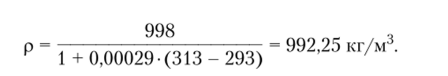

Задача 3. Определить изменение плотности нефти при сжатии се от давления р = 1 • 10⁵ до/?з⁼ 1 • Ю^г,Па, если коэффициент объемного сжатия нефти p_v = 7,4 10^MO Па'¹.

Решение. Коэффициент объемного сжатия определяется по формуле:

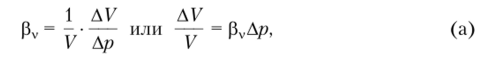
где V— объем жидкости при давлениир, AV— изменение объема жидкости при ее сжатии.

Разность давлений будет: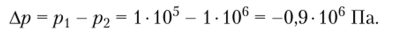

Плотность нефти находится, но формуле: 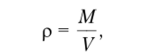где М — масса нефти.

Так как в процессе сжатия масса нефти остается неизменной, то где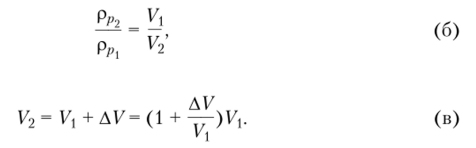

Формула (в) с учетом (а) будет:

Подставляя (г) в (б), получаем: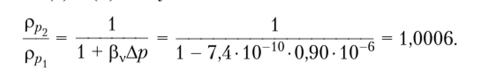

Следовательно, плотность нефти с изменением давления от К) ' до 10^г> Па изменяется незначительно.

Задачи для самостоятельного решения к главе 1.

Задача 1. Цилиндрический сосуд заполнен нефтью до высоты h = 2 м при температуре t = 32 °C. Определить высоту уровня нефти Л₂ при снижении температуры до 1₂ = 5 °C. Изменение объема резервуара при уменьшении температуры не учитывать. Коэффициент температурного расширения нефти принять равным р_г = 0,0072 1/град.

Задача 2. В отопительной системе, включающей котел, радиаторы, трубопроводы при температуре ?, = 20 °C содержится V= 1 м³ воды. Найти увеличение объема воды при ее нагревании до ?₂ = 95 °C.

Задача 3. Найти коэффициент температурного расширения р, жидкости в количестве Q = 1 ()()()///, находящейся в цилиндрическом резервуаре диаметром d= 3 м и имеющей при температуре Т= 273 К плотность р = 800 кг/м³, если при увеличении температуры жидкости на Д7'= 20 К ее объем возрастает на AV = 5 м³

Задачи к главе 2.

Задача 1. Определить потери эксергии Д W теплоты в количестве q = 100 Дж при понижении температуры рабочего тела с Т = 1000 К до Т = = 500 К без совершения работы. Температура окружающей среды Г₂ = 293 .

Решение. Эксергия теплоты при температурах рабочего тела 1000 К и 500 К определяется по формулам:

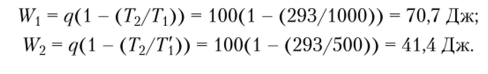
Задача 2. Определить потери КПД Ар цикла Отто по сравнению с КПД цикла Карно, реализуемых в диапазоне температур 7) = 1500 К и Т₀ = 280 К. Температуру в конце адиабатного расширения в цикле Отто принять равной Т = 800 К (см. рис. 2.11).

Решение. КПД циклов Карно pf и Отто р" определяются соответственно по формулам:

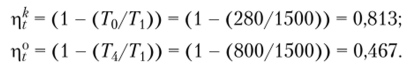
Потеря КПД в цикле Отто по сравнению с циклом Карно составляет:

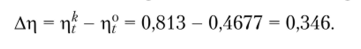
Задачи к главе 3.

Задача 1. Определить угол наклона политропы, а (см. рис. 3.15) для изобары (р = const) и изохоры (v = const).

Решение. Показатель политропы определяется по формуле п = tga. Так как в изобарном процессе, исходя из формулы pv" = const, п = 0, то угол a = 0. В изохорном процессе п ± °о и, следовательно, угол a = 90°.

Задача 2. Теоретически доказать, что изотерма расширения идеального газа является более пологой кривой в рп-координатах, чем адиабата, в заданном интервале изменения объема.

Решение. В адиабатном процессе расширение газа происходит при отсутствии теплообмена с окружающей средой. Следовательно, работа выполняется лишь за счет уменьшения внутренней энергии рабочего тела. В изотермическом процессе для обеспечения постоянной температуры при расширении газа к рабочему телу подводится теплота, компенсирующая убыль внутренней энергии. Поэтому при одинаковом объеме давление в конечной точке изотермического процесса будет больше давления адиабатного процесса. И следовательно, изотерма будет более пологой кривой.

Задачи к главе 4.

Задача 1. Изобразить в pv- и 7s-координатах изохору, изобару, изотерму и адиабату, исходящие из некоторой точки 1 в области влажного пара.

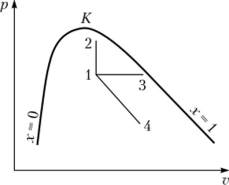
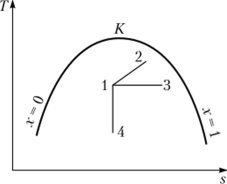
Рис. П. 1. дн-диаграмма Рис. П. 2. 7л'-диаграмма Решение. Кривые перечисленных процессов в указанных координатах приведены на рис. П. 1 и П. 2.

На рис. П. 1 и П. 2 приведены следующие процессы: 1—2 — изохорный; 1—3 — изобарный и изотермический; 1—4 — адиабатный.

Задача 2. Объяснить, что понимается под аномальностью воды и как влияет это ее свойство на изображение фазовых переходов в рТ- и /w-координатах.

Решение. Под аномальностью воды понимается ее свойство, состоящее в том, что она имеет максимальную плотность при температуре t = 4 °C. Следовательно, в диапазоне температур от t = 0 °C до t < 4 °C вода имеет мйныную плотность, чем при температуре 4 °C. Поэтому, после того как она охлаждается до температуры, меньше 4 °C, более холодная вода перемещается к поверхности (как имеющая меньшую плотность и, следовательно, более легкая), а более теплая вода оказывается в нижней части емкости (водоема). Именно этим свойством воды объясняется ее замерзание с поверхности.

Аномальность воды в рТ- и /^-диаграммах отражается в том, что линия фазового перехода из твердого состояния (лед) в жидкое (вода) с повышением давления отклоняется в сторону меньших температур (влево) (см. рис. 4.1,4.2). Аномальность воды при построении TS-диаграммы не учитывается, что, однако, незначительно влияет на точность расчетов (см. рис. 4.3).

Задачи к главе 5.

Задача 1. Найти скорость истечения газа (кислорода) через суживающееся сопло, если давление на входе р = 8 • 10⁶ Па, а на выходе р₂ = 5* 10⁶ Па. Температура газа на входе в сопло Т = 293 К.

Решение. Учитывая, что р/р₂ ⁼ 0,625 превышает критическое отношение давлений р_кр = 0,528 (для двухатомного газа), скорость на выходе из сопла следует определять по формуле (5.11), которую можно представить в виде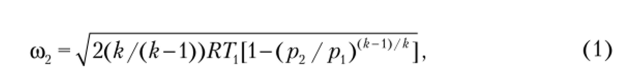

где k = 1,4 — показатель адиабаты; R = 259,8 Дж (кг* К) — удельная газовая постоянная для кислорода.

Подставляя исходные данные в (1), находим со₂ ⁼ 257,9 м/с.

Задачи к главе 7.

Задача 1. Определить количество воздуха п (моль), находящегося в цилиндре ДВС перед началом процесса сжатия в цикле Отто (см. рис. 7.2) при следующих исходных данных: р_{ = 80 000 Па; V_{ = 0,003 м³; Т = 293 К; 8=10, где pi, T_h V_{ — давление, температура и объем воздуха в точке 1; е — степень сжатия.

Решение. Количество воздуха в цилиндре определяется, но формуле: где = 8,314 ДжДмольК) — универсальная газовая постоянная.

Выражая из (1) п, находим.

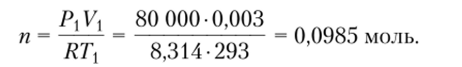
Задача 2. Найти температуру во всех точках цикла Тринклера (см. рис. 7.4) при следующих исходных данных: Т = 300 К; k = 1,4; X = 1,6; е = 9; р = 1,3, где Т — температура в точке 1; k — показатель адиабаты; X — степень повышения давления; 8 — степень сжатия; р — степень предварительного расширения.

Решение. Температура в точках цикла 2, 3, 4, 5 определяется по формулам: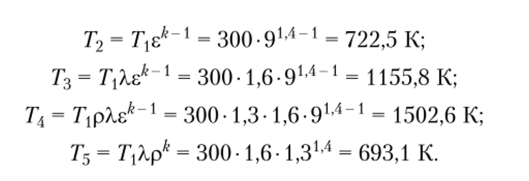

Задачи к главе 8.

Задача 1. Определить термический КПД цикла ГТУ с подводом теплоты при постоянном давлении с регенерацией теплоты при следующих исходных данных: р = 10; р = 6; k = 1,4, где р — степень повышения давления в компрессоре; р — степень изобарного расширения; k — показатель адиабаты. Степень регенерации принять равной: а = 0; 0,5; 1.

Решение. Термический КПД цикла ГТУ с регенерацией теплоты определяется по формуле:

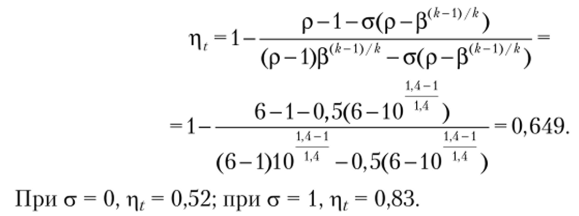
Задача 2. Найти температуры в точках 1, 2, 3, 4 цикла ГТУ с подводом теплоты при постоянном объеме и его термический КПД при исходных данных (см. рис. 8.6): Р = 8; X = 3; k = 1,4; Т = 300 К.

Решение. Температуры в указанных точках цикла находятся по формулам: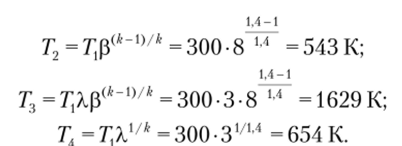

Формула для определения термического КПД цикла ГТУ через температуры в точках 1, 2, 3, 4 имеет вид:

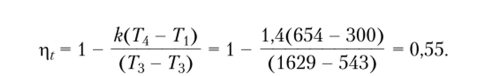
Термический КПД цикла можно также определить, но формуле:

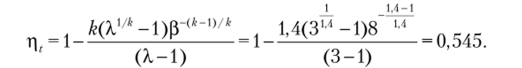
Как видно, термический КПД, найденный по двум различным формулам, практически равен одинаковой величине.

Задачи к главе 9.

Задача 1. Оценить влияние необратимости расширения пара в турбине иа термический КПД цикла Ренкина при следующих исходных данных (см. рис. 9.6): ц = 3500 кДж/кг; i₂⁼ 1996 кДж/кг; i₂ = 2225 кДж/кг; ц =115 кДж/кг; г₄ =125 кДж/кг.

Решение. Термический КПД цикла Ренкина без учета необратимости расширения пара в турбине находится по формуле:

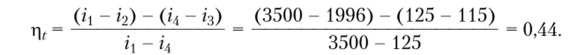
Формула для определения КПД с учетом необратимости расширения пара в турбине имеет вид:

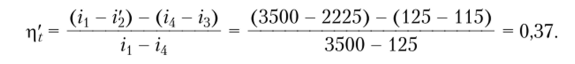
Таким образом, необратимое расширение пара в турбине по сравнению с адиабатным расширением пара снижает КПД цикла Ренкина (при заданных выше параметрах) на Дг| = г|_; — r|'_f = 0,44 — 0,37 = 0,007.

Задача 2. Найти теоретический удельный расход пара в кгДкВтч) и кг/МДж и удельный расход теплоты (кг/МДж) при следующих параметрах (см. рис. 9.4, 9.6): i = 3700 кДж/кг; i₂ = 2010 кДж/кг; г₃ = 120 кДж/кг.

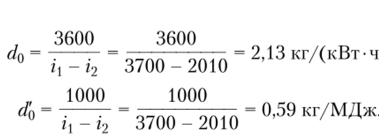
Удельный расход теплоты в кДж/МДж будет:

Решение. Удельный расход пара в кгДкВтч) и кг/МДж определяется по формулам:

);

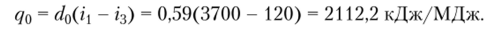
Задачи к главе 10.

Задача 1. Определить удельную холодопроизводителыюсть q₀, величину теоретической работы цикла / и холодильный коэффициент е паровой компрессорной холодильной установки при следующих параметрах работы (см. рис. 10.6): i = 540 кДж/кг; i₂ = 580 кДж/кг; г₄ = 420 кДж/кг.

Решение. Величины <�у₀> U ^? находятся, но формулам:

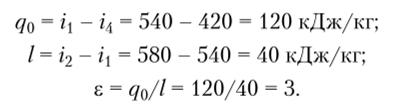
Задача 2. Для вихревой трубы, приведенной на рис. 10.10, найти величину понижения температуры At_x, если известно, что повышение температуры горячего потока Дt_r = 20 °C; р = 0,9.

Решение. Температура холодного потока определяется, но формуле:

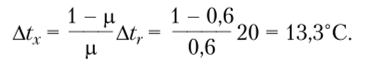
Задачи к главе 11.

Задача 1. Найти константу равновесия &_с реакции:

протекающей в условиях химического равновесия.

Решение. Для любой произвольной реакции:

протекающей в условиях химического равновесия, константа равновесия, согласно закону сохранения масс, определяется по формуле:

где С_л, С_в, С& С[) — концентрация веществ А, В, С, D; a, b, с, d — число молей веществ.

Используя формулу (3), константа равновесия реакции (1) записывается в виде: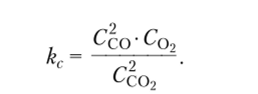

Задача 2. Определить состав смеси химической реакции:

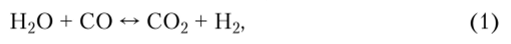
если концентрации отдельных веществ при химическом равновесии составляют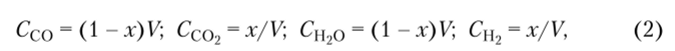

где V — общий объем смеси; х — доля моля вещества.

Примем, что в начале реакции были 1 моль СО и 1 моль Н₂0, а константа равновесия k_c = 1.

Решение. Формула для константы равновесия реакции (1) имеет вид: 444.

Подставляя концентрации отдельных веществ (2) в соотношение (3), находим: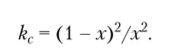

Учитывая, что k_c = 1, получаем:

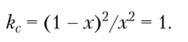
Отсюда находим долю моля вещества х = 0,5.

Следовательно, состав смеси при равновесии будет: СО — 0,5 моля; Н₂0 — 0,5 моля; С0₂ — 0,5 моля; Н₂ — 0,5 моля.

Раздел II Задачи к главе 2.

Задача 1. Показать, что граничные условия третьего рода в зависимости от величины коэффициента теплоотдачи могут быть сведены к граничным условиям первого и второго рода.

Решение. Выполним анализ формулы для граничных условий третьего рода: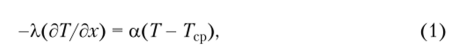

где Т — температура; х — координата; А. — коэффициент теплопроводности; а — коэффициент теплоотдачи; Т_ср — температура среды.

Представим формулу (1) в виде: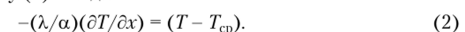

Из формулы (2) следует, что при больших значениях, а (а -*? °°) левая часть формулы будет приближаться к нулю (~(к/а)(дТ/дх) —* 0). Следовательно, температура на границе будет равна температуре среды Т = Т_ср, т. е. получаем условия теплового удара (граничное условие первого рода).

Анализируя формулу (1), можно заметить, что при, а —*? 0 она приводится к виду -(дТ/дх) = 0, что эквивалентно граничному условию адиабатной стенки, т. е. граничному условию второго рода при тепловом потоке q = 0.

Для всех, а в диапазоне 0 < а < оо, т. е., когда правая часть соотношения (1) имеет некоторую конкретную величину q = а (ТТ_ср), формула (1) приводится к граничному условию второго рода -Х (дТ/дх) = q.

Задачи к главе 3.

Задача 1. Найти точное аналитическое решение стационарной задачи теплопроводности для двухслойной стенки в следующей математической постановке:

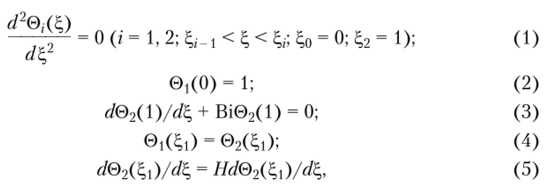
где 0 = (ГГ_ср)/(Г_ст — Гер); Bi = а5Д₂; ?, ⁼ х/8; Н = Х₂/Х, Г— температура;^р — температура среды; Т" — температура стенки; а — коэффициент теплоотдачи; Д₂ — коэффициенты теплопроводности; 5|, 8₂ — толщины слоев; 5 = 8]+ 8₂; Bi — число Био; 0 Д — безразмерные температура и координата.

Решение. Решение задачи (1)—(5) принимается в виде:

где С, С₂₁, С|₂, С— неизвестные коэффициенты.

Очевидно, что соотношения (6), (7) удовлетворяют уравнению (1). Подставляя (6), (7) в граничные условия (2) — (5), относительно неизвестных коэффициентов будем иметь систему четырех алгебраических линейных уравнений. После решения этой системы соотношения (6), (7) принимают вид: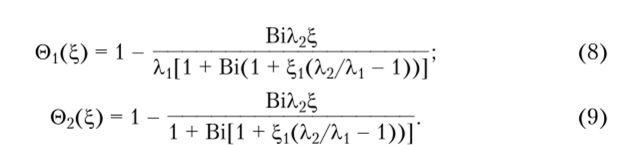

Соотношения (8), (9) представляют точное аналитическое решение задачи (1)—(5), в чем можно убедиться непосредственной подстановкой.

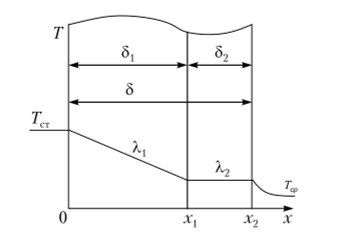
Рис. II3. Схема теплообмена в двухслойной стенке Задача 2. Используя решение (9) задачи 1, путем решения обратной задачи теплопроводности найти толщину первого слоя по известной из эксперимента температуре на внешней поверхности стенки Т₂(х₂) = 343 К при следующих исходных данных: = 2 Вт/(мК); Х₂ = 45 ВтДмК); S₂ = = 0,005 м; Г_ст = 375 К; Т_ср = 273 К; а = 20 ВтД м² • К).

Решение. Запишем соотношение (9) в размерном виде.

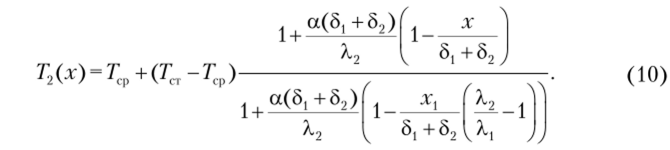
Подставляя Т₂{х₂) в левую часть соотношения (10), положив х = Sj + S₂, относительно неизвестной величины 8] получаем алгебраическое уравнение, из решения которого находим 8] = 0,04 м.

Задача 1. Используя метод Трефтца, найти решение задачи теплопроводности для квадрата в следующей математической постановке (рис. П.4):

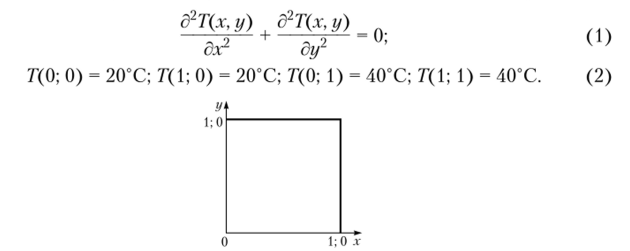
Рис. П. 4. Схема теплообмена к задаче 1.

Решение. Решение задачи (1), (2), следуя методу Трефтца, принимается в виде:

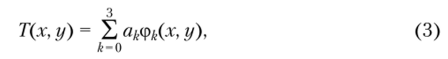
где а/_; — неизвестные коэффициенты; срД. г, у) — координатные функции.

В качестве координатных принимаются следующие функции:

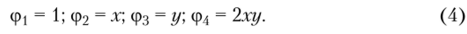
Очевидно, что при использовании в качестве координатных функций (4) соотношение (3) при любых значениях неизвестных коэффициентов a* (k = 0,1, 2,3) точно удовлетворяет уравнению (1). Для нахождения неизвестных а/, подставим (3) (с учетом 4) в граничные условия (2):

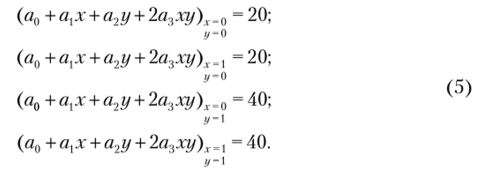
Соотношения (5) представляют систему четырех алгебраических линейных уравнений относительно неизвестных я₀, а, а₂, а^. Решение системы уравнений (5) имеет вид: я₀ = 20; а —20; а₂ = 40; а₂ = 0.

Соотношение (3) с учетом найденных значений неизвестных коэффициентов = (k = 0, 3) будет: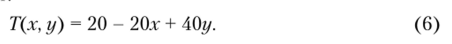

Соотношение (6) точно удовлетворяет уравнению (1) и граничным условиям (2). Найдем, например, температуру в точке х = 0,5; у = 0,5 (центр квадрата). Используя (6), находим Г (0,5; 0,5) = 30 °C. Отметим, что координаты в данном случае приняты в безразмерном виде х = ц/8; у = %/8, где 8 — размер стороны квадрата, м; ц, — размерные координаты.

Задача 1. Используя ортогональный метод Л. В. Канторовича, найти точное аналитическое решение нестационарной задачи теплопроводности для бесконечной пластины в следующей математической постановке:

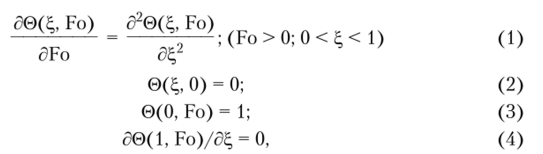
где 0 = (Г — 7о)/(Г_ст — 7'о); Fo = at/8²] ?, = х/5; 0, Fo, ?, — соответственно безразмерные температура, время, координата; Т₀ — начальная температура; Т_ст — температура стенки; Г— температура; а — коэффициент температуропроводности; t — время; 5 — толщина пластины; х — координата.

Решение. Решение задачи (1)—(4) принимается в виде:

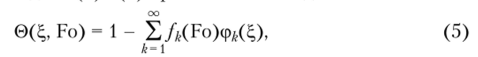
где/ДТо) — неизвестные функции времени; срД^) = sin (m^/2) (r=2k- 1) — координатные функции, в любом приближении точно удовлетворяющие граничным условиям (2)—(4).

Составляя невязку уравнения (1) и требуя ее ортогональности ко всем координатным функциям <�р/,(?,) (к = 1, °°), находим:

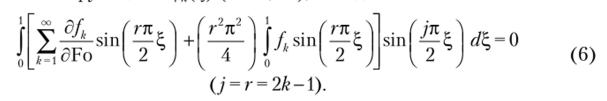
Соотношение (6) с учетом ортогональности синусов приводится к виду.

Интегрируя уравнение (7) и подставляя найденное решение в (5), получаем: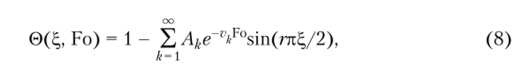

где г>к = г²к²/4 (г = 2к — 1); А_к — константы интегрирования, определяемые из начального условия (2). Для этого составляется его невязка и требуется ее ортогональность ко всем координатным функциям <�рД%) (к = 1, °о):

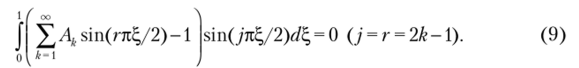
Соотношение (9) относительно Л, представляет бесконечную систему алгебраических линейных уравнений. Ввиду ортогональности синусов неизвестные в системе разделяются и она приводится к одному уравнению:

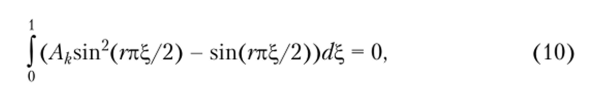
из решения которого получаем Л* = 4/(га) (& = 1, °°).

С учетом найденных значений А^ соотношение (8) представляет точное аналитическое решение задачи (1)—(4). Оно совпадает с решением аналогичной задачи, полученным в [49] методом разделения переменных.