Сигналы с линейной частотной модуляцией

Сигналы с внутриимпульсной частотной модуляцией относятся к особому классу модулированных сигналов, широко применяющихся в системах связи, измерительной технике и других областях. Они привлекли внимание специалистов прежде всего в связи с поисками способов сжатия импульсных сигналов. Эти сигналы отличаются от обычных радиоимпульсов (отрезков несущего колебания) тем, что их высокочастотное заполнение имеет переменную частоту. Чаще всего используется внутриимпульсная частотная модуляция с линейным законом изменения мгновенной частоты во времени.

Принцип создания сигналов с линейной частотной модуляцией (ЛЧМ). При модуляции частоты несущего колебания по негармоническому закону определение спектра сигнала резко усложняется. Проведем анализ радиоимпульса с огибающей прямоугольной формы, у которого частота несущей линейно нарастает от начала импульса к его концу (рис. 2.42). Конкретизируя математическую модель сигнала с переменной частотой заполнения, предположим, что его длительность равна т_и, причем середине импульса соответствует точка t = 0, а мгновенная частота изменяется, но линейному закону (рис. 2.42, а)

Здесь со₀ — несущая частота немодулированного сигнала u_u{t) = = f/_ncos ((o/ + <�р₀); параметр, а [с^-2] характеризует скорость изменения частоты модулированного колебания.

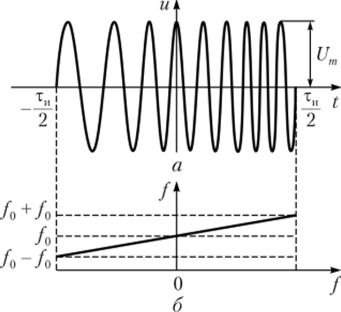
Рис. 2.42. Радиоимпульс с ЛЧМ:

а — графическое представление сигнала; б — закон изменения частоты За время, равное длительности импульса, девиация частоты (рис. 2.42,6)

Для упрощения анализа примем ср₀= 0, поскольку наличие этого сдвига несущественно. Тогда интегрирование соотношения (2.92) даст мгновенную (полную) фазу сигнала в любой момент времени по длительности импульса: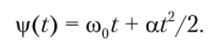

Итак, импульсом с линейной частотной модуляцией (ЛЧМ-сигналом) назовем сигнал, описываемый следующими соотношениями:

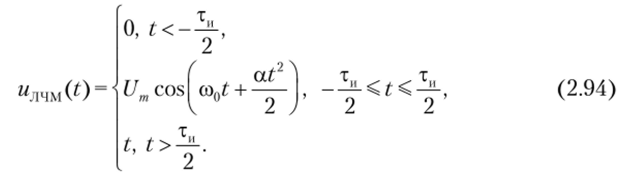
Отметим очень полезное свойство ЛЧМ-сигналов. Пусть некоторое электронное устройство осуществляет временную задержку входного сигнала, величина которой зависит от частоты колебаний. Если с ростом частоты время задержки уменьшается, то при определенных условиях, подавая на вход устройства импульс достаточно большой длительности, можно «сжать» его во времени. Этот эффект обусловлен тем, что на выходе устройства задержки, как низкочастотные составляющие, относящиеся к началу импульса, так и более высокочастотные, находящиеся в его конце, будут появляться одновременно.

Спектр ЛЧМ-импульса прямоугольной формы. Используя формулу (2.94) и формулу Эйлера, получаем спектральную плотность ЛЧМ-импульса:

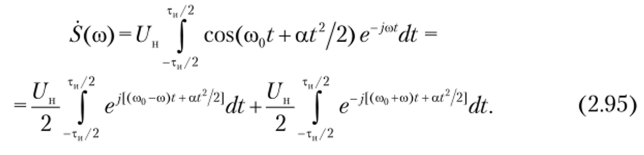
Первый интеграл в правой части формулы (2.95) описывает спектральную плотность с резко выраженным максимумом в области положительных частот, близких к со₀. Второй интеграл соответствует всплеску спектральной плотности вблизи частоты со = со₀. Интерес представляет случай, когда эффект перекрытия спектров, концентрирующихся при положительных и отрицательных частотах, невелик и близок к нулю. Это связано с тем, что девиация частоты со_л за время длительности импульса очень мала по сравнению с несущей частотой со₀, т. е. со_д = ат_н со₀.

Поэтому в формуле (2.95) достаточно вычислить только первый интеграл, дающий спектральную плотность при частотах со > 0. Аргумент экспоненциальной функции в первом слагаемом формулы (2.95) целесообразно дополнить до полного квадрата разности. Тогда после несложных преобразований получим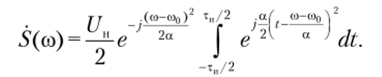

Перейдем от переменной t к новому аргументу х, выполнив замену.

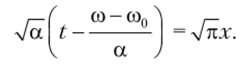
т.

После вычислений запишем.

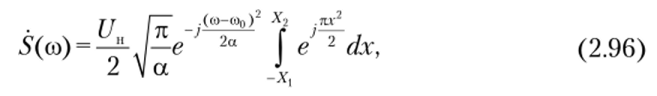
где пределы интегрирования.

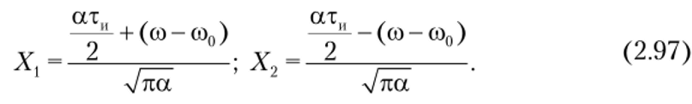
Для дальнейшего анализа ЛЧМ-сигнала используем интегралы Френеля.

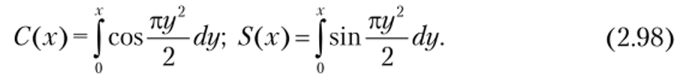
Подставив формулы (2.97) и (2.98) в соотношение (2.96), получим окончательное выражение для спектральной плотности ЛЧМ-сигнала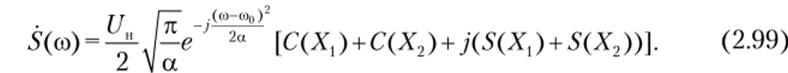

Представим соотношение (2.99) в показательной форме: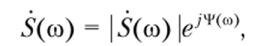

где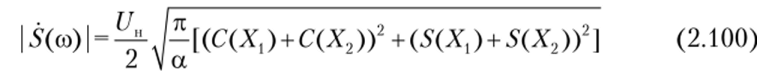

— амплитудный спектр (модуль спектральной плотности);

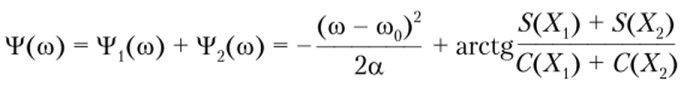
— фазовый спектр.

Составляющую фазового спектра ЛЧМ-сигнала.

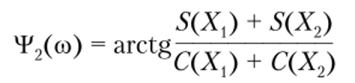
называют остаточным фазовым членом.

ЛЧМ-сигналы с большой базой. Характер частотной зависимости модуля и фазы спектральной плотности ЛЧМ-импульса связан с числом.

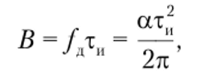
называемым базой ЛЧМ-сигнала.

Эти особенности ЛЧМ-сигналов связаны со следующим. Во-первых, амплитудный спектр практически постоянен в пределах полосы частот (—(о_д/2, со_л/2) с центром в точке со₀. Соответствующие графики амплитудного спектра и остаточного фазового члена, построенные по вышеприведенным формулам, показаны на рис. 2.43.

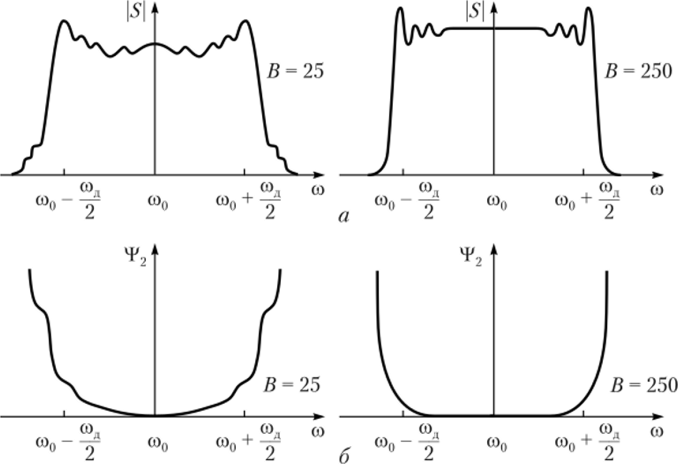
Рис. 2.43. Спектральная плотность ЛЧМ-сигнала при различных значениях базы:

а — амплитудный спектр; б — частотная зависимость остаточного фазового члена Во-вторых, осцилляции амплитудного спектра существенно уменьшаются с увеличением базы ЛЧМ-сигнала вплоть до теоретически полного исчезновения.

Анализ формулы (2.100) показывает, что на частоте спектра со₀

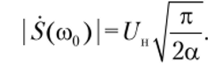
Таким образом, амплитудный спектр ЛЧМ-сигнала с большой базой.

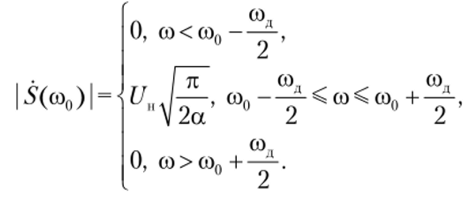
Энергетический спектр такого сигнала, определяемый согласно формуле (2.60) как.

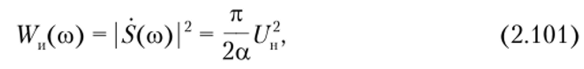
также постоянен в полосе частот (со₀ — со_д/2, со₀ + со/2) и равен нулю вне ее.

Пример 2.8.

Определим параметры спектра прямоугольного ЛЧМ-импульса, у которого амплитуда U_n = 10 В, длительность т_н = 5 мкс, циклическая частота несущей нсмодулированного сигнала/₀ = 5 ГГц, девиация частоты несущей^ = 50 МГц.

Решение

База анализируемого ЛЧМ-сигнала В =/_дт_и = 50 -10⁶* 5 * 10 ⁶ = 250. Из соотношения (2.93) вычисляем скорость нарастания частоты ЛЧМ-импульса, а = = 2я/д/т_и = 6,28−50−10⁶/(5−10″⁶) = 6,28−10¹³ с"². Согласно формуле (2.101) энсргетический спектр Wj_f(co) = 3,14* 100/(12,56−10^u) = 2,5*10 ¹². Поскольку база сигнала достаточно велика, то амплитудный и энергетический спектры расположены в полосе частот от /₀ — fJ2 = 4,975 ГГц до /₀ + /_д/2 = 5,025 ГГц.

Автокорреляционная функция (АКФ) ЛЧМ-сигнала. Для упрощения анализа положим, что база ЛЧМ-сигнала достаточно велика, и поэтому его энергетический спектр равномерен и расположен лишь в полосе (со₀ — со_д/2, со₀ + со_л/2) вокруг несущей частоты со₀. Тогда согласно выражению (2.61) АКФ ЛЧМ-сигнала равна.

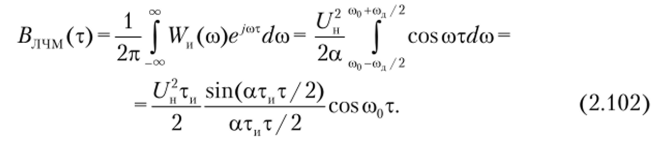
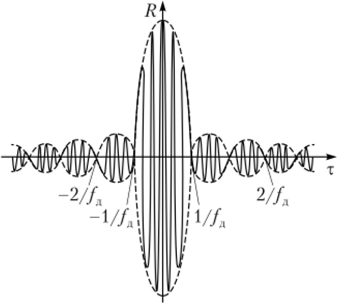
Рис. 2.44. График нормированной АКФ ЛЧМ-импульса.

График нормированной АКФ ЛЧМ-импульса R (т) = Л_лчм(т)/В_лчм(0) показан на рис. 2.44.

Формула (2.102) устанавливает важное свойство ЛЧМ-сигнала — ширина главного лепестка огибающей АКФ обратно пропорциональна девиации частоты несущей /_л. Это объясняется тем, что огибающая АКФ ЛЧМ-сигнала первый раз обращается в нуль при сдвиге сигнала относительно копии на х =.

= 27х (ат₁₁) = 1//_д. Применяемые в специальных системах связи ЛЧМ-сигналы характеризуются значительной девиацией частоты, поэтому главный лепесток АКФ получается узким, что полезно. Однако с точки зрения корреляционных свойств ЛЧМ-сигналам присущ недостаток — высота двух первых симметричных боковых лепестков АКФ велика (0,212 от высоты центрального). При значительном шумах приемника это может привести к ошибочному определению временного положения импульса. Если же энергетические потери в устройстве сжатия малы, то амплитуда выходного сигнала может превысить уровень шумов.