Интеграция алгебраического и графического методов в решении уравнений, неравенств и их систем

Под интеграцией алгебраического и геометрического (графического) методов будем понимать процесс сочетания или связи (слияния) данных методов, осуществляемый учеником путем перевода учебной информации с алгебраического языка на геометрический или с геометрического языка на алгебраический и обратно.

Под сочетанием алгебраического и геометрического методов будем понимать одновременное использование их на одном уроке при решении задачи, доказательстве теоремы, а также при введении нового понятия или правила.

Решение квадратных уравнений и неравенств

Историческая справка Квадратные уравнения и способы их решения были известны в глубокой /(ревности. Так ещё за две тысячи лет до нашей эры задачи измерения земельных участков приводили древних вавилонян к решению квадратных уравнений.

В древней Греции (Пифагор. Евклид) квадратные уравнения решались геометрическим методом.

Знаменитый узбекский математик аль-Хорезми решал квадратные уравнения как алгебраическим, гак и геометрическим методами.

Так как общая формула решения квадратных уравнений тогда ещё не была выведена, то аль-Хорезми приводит решения шести различных видов квадратных уравнений, например:

• 1. Один квадрат равен корням (х~ = ах).
• 2. Один квадрат и корни равны числу (хГ + ах = Ь).
• 3. Один квадрат и число равны корням (х~ + а = Ьх) и т. д.

Приведем примеры решения уравнений аль-Хорезми алгебраическим и геометрическим методами.

Пример 1.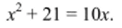

Алгебраический метод

• 1. Раздели число корней пополам: 10:2 = 5.
• 2. Умножь это число само на себя: 5 • 5 = 25.
• 3. Вычти из него число: 25−21 =4.
• 4. Извлеки квадратный корень: 75 = 2.
• 5. Этот корень прибавь к половине корней или вычти из неё: 5 + 2 = 7; 5- 2 = 3.

Если записать все приведенные действия одной формулой, то получим:

Как видим решение аль-Хорезми полностью совпадает с современным решением по формуле. Приведем пример геометрического решения уравнения.

Пример 2. Решить уравнение.

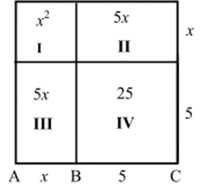
Рис. 5.

х² + 10. г = 39.

Решение.

Геометрический метод Пусть отрезок ЛВ = х, а отрезок ВС = 5 (рис. 5). Строим квадрат со стороной, равной л' + 5, и разбиваем его на четыре участка, как показано на рисунке. Площадь квадрата равна (.v + 5)‘. С другой стороны, площадь участков I, II и III равна 25. Значит, площадь всего квадрата равна 39 + 25 = 64. Отсюда имеем:

(л + 5)² =64, л + 5 = 8, * = 3.

Задачи, приводящие к квадратным уравнениям, имеются в старинных кигайекмх и индийских матсмашчсских трактах.

В современной школе квадратные уравнения и неравенства изучаются по действующей программе в 8 классе, изолированно друг от друга. Причем, в учебниках квадратные уравнения решаются только аналитически, по формулам или путем выделения квадрата двучлена, графический метод решения таких уравнений не рассматривается. Например, в учебнике «Алгебра. 8 класс», автор Ш. А. Алимов (и др.), квадратичная функция и её график, необходимые для решения квадратных уравнений графическим методом, изучаются после темы «Квадратные уравнения». Аналогично обстоит дело и в учебнике «Алгебра. 8 класс», автор Ю. Н. Макарычев (и др.), где представлен только аналитический метод решения квадратных уравнений. Такой односторонний подход нс способствует формированию целостных знаний учащихся о решении квадратных уравнений и отрицательно сказывается на формировании их образного мышления.

По иному представлен вопрос о методах решения квадратных уравнений в учебнике «Алгебра. 8 класс» А. Г. Мордковича. Автор рассматривает графический метод решения квадратных уравнений раньше алгебраического и знакомит учащихся с разными способами этого метода. В соответствии с этим квадратичная функция и её график изучаются до введения понятия квадратного уравнения. Обосновывая данный факт, А. Г. Мордкович пишет: «Графический (или, точнее, функционально-графический) метод решения уравнений, на наш взгляд, должен всегда быть первым и одним из главных при решении уравнений любых типов. Неудобства, связанные с применением графического метода, как правило, и создают ту проблемную ситуацию, которая приводит к необходимости отыскания алгоритмов аналитических способов решения уравнения» [13, с.11].

Заметим, что прежде, чем решать квадратные уравнения и неравенства графическим методом, необходимо провести специальную подготовительную работу. В восьмом классе после ознакомления учащихся с квадратичной функцией и её графиком следует рассмотреть какую-либо задачу, которая привела бы учеников к пониманию квадратного уравнения как равенства двух функций от одного и того же аргумента, например:

Задача. Квадрат периметра прямоугольника, основание которого больше высоты на 1 см, больше площади этого прямоугольника на 34 см. Найдите высоту прямоугольника.

В ходе решения учащиеся приходят к выводу, что площадь прямоугольника равна х (д- + 1) см², а периметр равен (4л* + 2) см, тогда квадрат периметра равен (4.v + 2)~ см². Так как по условию задачи квадрат периметра прямоугольника больше площади прямоугольника на 34 см", то можно составить уравнение:

х (х+ 1) + 34 = (4д- + 2)²

После преобразований получаем следующее квадратное уравнение:

д;² + л: — 2 = 0.

Корнями полученного уравнения являются х = 1 и х₂ = - 2. Так как длина отрезка не может быть отрицательным числом, то искомая высота равна 1 см. Вместе с этим каждое из выражений уравнения.

х (х + 1) + 34 = (4.v + 2)² или *²+* + 34= 16л:² + 16. V + 4.

можно рассматривать как функцию у = X² + х + 34 и у = 1 блг² н- 16д- - 30. Для каждой из них можно построить график. Если графики построить в одной системе координат, то они пересекутся. Абсциссы точек пересечения Х = 1и *2 = - 2 дают то значение аргумента, при котором данные функции равны (у (1) = 36 и у (- 2) = 36). Но так как нам надо найти высоту прямоугольника, а длина отрезка отрицательной быть не может, то искомая высота принимает значение х = 1.

Можно рассмотреть другие задачи, подобные данной, решение которых приводит к квадратным уравнениям. Таким образом, учащиеся приходят к выводу, что квадратные уравнения, как и уравнения первой степени с одной переменной, тоже могут решаться геометрическим (графическим) методом.

Приведем примеры параллельного решения квадратных уравнений и неравенств алгебраическим и графическим методами.

ПримсрЗ. Решить квадратное уравнение х² — 4х + 3 = 0 и соответствующие ему неравенства: х² — 4х + 3 > 0 и х² — 4х + 3 < 0.

Решение./. Алгебраический метод

х — 4х + 3 = 0, по общей формуле корней квадратного уравнения имеем:

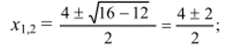
откуда = 3, *2 — 1 • О т в с т: Х] = 3, х₂ = 1.

II. Графический метод (I способ)

Построим график функции у = х²-Лх + 3. Построение будем проводить по следующей схеме:

1) Найдем координаты вершины параболы и уравнение оси параболы.

fo _а 1.

Имеем а = 1, b = -4, тогдаХо =—=—= 2; уо = /(2) = 2‘ - 4−2 + 3 = - 1. Значит,.

2 а 2

вершиной параболы является точка (2; -1), а осью параболы — прямая х = 2.

2) Возьмем какую-нибудь точку, принадлежащую параболе, например, (0; 3) и построим ей симметричную относительно оси, получим точку (4; 3).

3) Через полученные три точки (2; -1), (0; 3), (4; 3) проводим параболу (рис. 6). Корнями уравнения X² — 4х + 3 = 0 служат абсциссы точек пересечения.

Рис. 6.

параболы с осью ОХ. Таких точек две: (1; 0) и (3; 0). Итак, х = 1, х₂ = 3.

Решив графическим методом уравнение, решаем сразу же соответствующие ему неравенства: дг² — 4х + 3 > 0 и х² — 4х + 3 < 0, используя построенный график. Решить данные неравенства графически — это значит ответить на вопрос, при каких значениях х ординаты точек параболы положительны (для первого неравенства) и отрицательны (для второго неравенства). Из рисунка 6 видим, что график функции расположен выше оси.

ОХ при х < 1 и при х > 3.

Значит, решениями неравенства х² — 4х + 3 > 0 служат все точки, принадлежащие промежуткам х < 1 и х > 3.

Аналогично, для неравенства х² — 4х + 3 < 0 замечаем, что график функции расположен ниже оси ОХ при 1 <�х < 3. Этот промежуток и является решением неравенства.

Для проверки полученных ответов решаем неравенства х² — 4х + 3 > 0 и х² — 4х + 3 < 0 аналитически, с помощью системы неравенств или методом интервалов (после его изучения).

После решения двух (трех) аналогичных уравнений и соответствующих им неравенств учащиеся могут сделать выводы по геометрической интерпретации их решений, а именно:

1. Если квадратное уравнение ах² + Ьх + с = 0 имеет два корня, то геометрически это означает, что парабола — график функции у = ах² + Ьх + с — пересекает ось ОХ в двух точках, абсциссы которых и являются корнями данного уравнения. Верно и обратное:

если парабола — график функции у = ах² + Ьх + с — пересекает ось ОХ в двух точках, то квадратное уравнение ах² + Ьх + с = 0 имеет два корня, которыми являются абсциссы точек пересечения.

2. Если квадратное неравенство ах!² + Ьх + с > 0 (их² + Ьх + с < 0) имеет решения (но выполняется не при всех значениях х), то геометрически это означает, что часть параболы — графика функции у = ах² + Ьх + с-расположена выше (ниже) оси ОХ. Верно и обратное: если часть параболы — графика функции у = ах² + Ьх + с — расположена выше (ниже) оси ОХ, то это означает, что квадратное неравенство ах² + Ьх + с> 0 (ах² + Ьх + с < 0) имеет решения.

Следует заметить, что графический метод решения квадратных уравнений и неравенств включает, кроме рассмотренного, ещё четыре способа решения. Приведем их схемы.

II способ. Преобразуем уравнение к виду х² = Ах — 3, затем построим в одной системе координат графики функций у = х² и у = 4. v — 3. Корнями уравнения служат абсциссы точек пересечения параболы и прямой — графиков этих функций.

III способ. Преобразуем уравнение к виду х² + 3 = 4. v, затем построим в одной системе координат графики функций у = х² + 3 и у = Ах. Корнями уравнения являются абсциссы точек пересечения параболы и прямой — графиков этих функций.

IVспособ. Преобразуем уравнение к виду х² — Ах + А — 1 = 0 и далее X² — Ах + 4 = 1, т. е. (х — 2у = 1. Построим в одной системе координат параболу у—(х — 2)² и прямую у = 1. Корнями уравнения служат абсциссы точек пересечения графиков этих функций.

Vспособ. Разделив почленно обе части уравнения на х, получим 4 4.

дг-4± = 0и далее х-А = —. Построим в одной системе координат гипербо;

д; л;

лу у = — и прямую у = х — А. Корнями уравнения являются абсциссы точек.

X

пересечения графиков данных функций.

Пример 4. Решить квадратное уравнение Ах — Ах + 1 = 0 и соответствующие ему неравенства: Ах² — Ах + 1 > 0 и Ах — Ах + 1 < 0.

Решение./. Алгебраический метод

Ах² -Ах + 1 =0, по формуле корней квадратного уравнения имеем: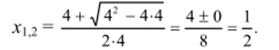

~ 1 Ответ: х= -.

II. Графический метод (I способ)

Построим график функции у = Ах~ - Ах + 1. Найдем сначала координаты вершины параболы: а = 4, b = - А, х₀ = ^ Уо ⁼ /(^) ⁼ 0.

Значит, вершиной параболы является точка (i; 0), а осью параболы прямая х =^. Так же как и в примере 3, выполняем построение графика (рис. 7).

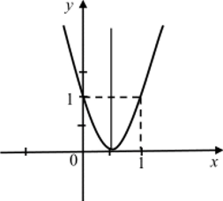
Как видим из рисунка, парабола имеет с осью ОХ только одну общую точку (i; 0). Значит, данное квадратное уравнение имеет только один 1.

корень: х = -.

Построенный график позволяет сразу же решить и квадратные неравенства: Ах² — Ах + 1 >0 и Ах² -Ах+КО.

Из рисунка видно, что вся парабола, кроме одной её точки, которая лежит на оси ОХ, расположена выше оси ОХ, поэтому решением первого неравенства служат промежутки х<^Х— и х> Второе неравенство нс имеет решений, так как ниже оси ОХ нет графика.

Для проверки полученных ответов решаем данные неравенства аналитически, путем разложения левой части на множители, аналогично тому, как мы делали это в примере 3.

После решения ещё двух (трех) аналогичных уравнений и соответствующих им неравенств учащиеся могут сделать выводы по геометрической интерпретации их решений, а именно:

/. Если квадратное уравнение ах² + Ьх + с = 0 имеет один корень, то геометрически это означает, что парабола — график функции у = ах¹ + Ьх + симеет с осью ОХ одну общую точку (то есть касается её) и абсцисса этой точки является корнем данного уравнения.

Верно и обратное:

если парабола — график функции у = ах² + Ьх + с — имеет с осью ОХ одну общую точку (то есть касается её), то квадратное уравнение ах² + Ьх + с — 0 имеет один корень, которым является абсцисса этой точки.

2. Если квадратное неравенство ах¹ + Ьх + с > 0 (ах + Ьх + с < 0) выполняется при всех х, кроме одного, то геометрически это означает, что вся парабола расположена выше (ниже) оси ОХ, кроме одной её точки, которая лежит на оси ОХ (т. е. парабола касается оси ОХ). Верно и обратное:

если парабола — график функции у = ах² + Ьх + с — касается оси ОХ, то квадратное неравенство ах² + Ьх + с > 0 (ах² + Ьх + с 0 (а < 0) выполняется при всех х, кроме одного — абсциссы точки касания, при, а 0) — решений нет.

Пример 5. Решить квадратное уравнение — дг² + 3д:-4 = 0и соответствующие ему неравенства: — х² + 3. v — 4 > 0 и — х² + 3* - 4 < 0.

Решение./. Алгебраический метод

- х² + Зх — 4 = 0, здесь а = -1, Ь — 3, с = - 4, тогда дискриминант этого уравнения равен: D = Ь² — 4ас = - 7. Так как D < 0, то данное квадратное уравнение не имеет корней.

II. Графический метод

Построим график функции у — - х² + Зх - 4. Найдем сначала координаты вершины параболы.

а = -1 (а < 0, значит, ветви параболы направлены вниз), Ь = 3,

Ь 3 3 7 3 7.

Хо=—=-, уо=/(-) = —. Значит, вершиной параболы является точка (-; —), а.

2а 2 2 4 2 4.

осью параболы — прямая^{х =}

Так же, как и в предыдущих примерах, выполняем построение графика, учитывая, что ветви параболы направлены вниз (рис. 8).

Как видно из рисунка, парабола не пересекает ось ОХ, значит, данное уравнение -х² + 3* - 4 = 0 не имеет корней.

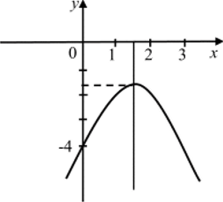
Рис. 8.

Решаем с помощью графика соответствующие неравенства:

-х² + Зд; - 4 > 0 и -х² + Зх — 4 < 0.

Рисунок показывает, что вся парабола лежит ниже оси ОХ, поэтому первое неравенство не имеет решений, а второе неравенство выполняется при всех х. Из графического решения учащиеся делают выводы:

1. Если квадратное уравнение ах² + Ьх + с = 0 не имеет корней, то геометрически это означает, что парабола — график функции у = ах + Ьх + с — не пересекает ось ОХ. Верно и обратное:

если парабола - график функции у = ах + Ьх + с — не пересекает ось ОХ, то квадратное уравнение ах² + Ьх + с = 0 не имеет корней.

2. Если квадратное неравенство ах² + Ьх + с > 0 (ах¹ + Ьх + с 0) выполняется при всех значениях х, то геометрически это означает, что парабола — график функции у = ах² + Ьх + с — расположена вся выше (ниже) оси ОХ

Если же указанное неравенство не имеет решений, то геометрически это означает, что парабола вся расположена ниже (выше) оси ОХ.

Уравнения и неравенства, сводящиеся к квадратным, можно решать аналогично, предварительно приведя их к квадратным. Приведем пример.

Пример 6. Решить уравнение х-3х + 2 = 2х-хи соответствующие ему неравенства: х² — Зх + 2 > 2х — х² и х² — Зх + 2 < 2х — х².

Решение./. Алгебраический метод

х² — Зх + 2 = 2х — х², преобразуем данное уравнение, перенеся все члены в левую часть:

.г² — Зх + 2 — 2х + х² = 0,.

после приведения подобных членов получим квадратное уравнение:

2х² — 5х + 2 = 0,

его корни находим по известной формуле:

• 5± J25−16 5 ±3 _Л 1
• 4 4 2

О т в е т: х = 2, х-> = -.

" 2.

II. Графический метод

Графически данное уравнение можно решить, не преобразовывая его, построив графики функций, стоящих в левой и правой частях уравнения, то есть Ух = х — Зх + 2 и у2 =2хх². Графиками данных функций являются две параболы. Построение их осуществляем по схеме, приведенной в примере 3.

Для первой функции у = х² — Зх + 2 находим:

b 3 _ч 1 / з 1 _ч

v₀=—= -, уо = /(дго) = —, значит, точка (-; —) является вершиной па;

2а 2 4 2 4.

раболы, а прямая л* = ^ - осью параболы.

Для второй функцииу₂=1х-х², то естьу₂ = -х² + 2х, имеем:

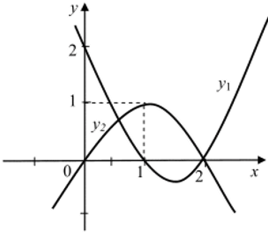
Рис. 9.

«го = —— = 1, уо — /Сто) = 1, значит, точка (1; 1) яв;

2а

ляется вершиной параболы, а прямая х = 1 — осью параболы. Затем осуществляем построение графиков функций (рис. 9). Абсциссы точек пересечения графиков дают корни исходного урав;

1 ч нения: .Vi = - ,*•> = 2.

Используя рисунок, решаем неравенства: х² — Зх + 2 > 2х-х² и х² — З. г + 2 < 2х-X¹.

Решить первое (второе) неравенство — на геометрическом языке означает, найти те значения х, при которых график функции у расположен выше (ниже) графика функции у₂. Из рисунка получаем ответ: х < 0,5, х> 2 (0,5 <*< 2).

В приведенных примерах интеграция алгебраического и геометрического методов преследует цель, показать учащимся графическую интерпретацию решения квадратного уравнения в случае, если оно имеет два корня (парабола пересекает ось ОХ в двух точках), один корень (парабола имеет с осью ОХ одну общую точку, касается её), не имеет корней (парабола не пересекает ось ОХ).

Аналогично, дастся графическая интерпретация решения квадратных неравенств, соответствующих данному квадратному уравнению, что приводит к укрупнению дидактических единиц (квадратные уравнения и неравенства рассматриваются одновременно). В ходе решения осуществляется постоянный перевод информации с алгебраического языка на геометрический и обратно, что влияет на развитие как понятийно-логического, так и эмоционально-образного типов мышления. В результате сопоставления выполняемых алгебраических и геометрических действий осуществляется контроль за ходом решения, а также прогнозирование некоторых результатов.