Десятичная запись приближенных чисел. 
Действия над приближенными числами

Приближенное число может быть целым или записываться в виде десятичной дроби. Установим такой способ записи приближенного числа х, при котором по его записи можно узнавать погрешность.

Определение 1.6. Значащими цифрами числа называются все цифры его десятичной записи, кроме нулей, стоящих перед первой цифрой, отличной от нуля.

Теперь дадим определение верной цифры.

Определение 1.7. Цифра а называется верной, если абсолютная погрешность приближенного числа не превышает половины единицы того разряда, в котором записана цифра а.

Принимается за правило при десятичной записи приближенного числа писать только верные цифры. Если известно, что данное приближенное число записано правильно, то по его записи сразу можно определить предельную абсолютную погрешность. Именно, при правильной записи абсолютная погрешность не превышает половины единицы низшего разряда. Например, если даны приближенные числа, записанные верно: а = 8,6; b = 0,0375; с = 2370, то их предельные абсолютные погрешности соответственно таковы: h_a = 0,05; fy, = 0,5; h_c = 0,5.

Замечание 1.4. Цифры, не являющиеся верными, называются сомнительными. Иногда при вычислениях целесообразно кроме верных значащих цифр сохранять еще одну сомнительную.

Замечание 1.5. Если приближенное число записано с некоторым числом десятичных знаков после запятой, причем последние десятичные знаки есть нули, являющиеся верными цифрами, то их не следует отбрасывать, т. е. их следует писать.

Например, если h_a < 0,5, то вместо а = 8,6 следует писать а — 8,600.

Очень часто число, точное или приближенное, содержит в своей записи цифр больше, чем это необходимо. В таких случаях производят округление.

Правило округления. Чтобы округлить число до п значащих цифр, отбрасывают все цифры, стоящие справа от п-й значащей цифры, или, если это нужно для сохранения разрядов, заменяют их нулями. При этом если первая из отброшенных цифр больше или равна пяти, то последнюю оставленную цифру увеличивают на единицу.

Очевидно, что при применении правила округления погрешность, вызванная округлением, не превышает половины единицы десятичного разряда, определяемого последней оставленной значащей цифрой.

Таким образом, по числу верных десятичных знаков в записи числа можно судить об абсолютной погрешности.

Оказывается, что по числу значащих цифр можно судить и об относительной погрешности. Возьмем число а = 8,6. Пусть все цифры верные. Тогда.

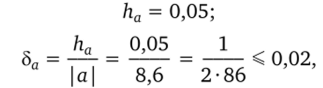
т.е. можно принять 5_а = 2%. Очевидно, что для любого числа с тем же набором значащих цифр (8, 6), расположенных в том же порядке (86; 0,86 и т. д.), относительная погрешность будет одной и той же, т. е. 2%.

Из вышесказанного следует такое правило.

Правило вычисления относительной погрешности. Пусть в записи приближенного числа все цифры верные. Предельную относительную погрешность можно принять равной дроби, числитель которой равен единице, а знаменатель есть удвоенное целое число, записанное при помощи всех значащих цифр данного числа с сохранением порядка их записи.

Пример 1.2.

Дано число а = 53,8, все цифры которого значащие. Найдите его предельную относительную погрешность.

Решение

По правилу вычисления относительной погрешности получаем 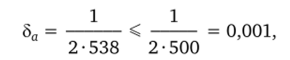или 8_а = 0,1%.

При выполнении арифметических действий над приближенными числами мы также получаем приближенное число. Сформулируем правила, позволяющие в сочетании с формулами (1.2) и (1.3) определить абсолютные и относительные погрешности результата.

Теорема 1.1. Предельная абсолютная погрешность суммы нескольких чисел или разности двух чисел равна сумме их предельных абсолютных погрешностей.

Теорема 1.2. Предельная относительная погрешность произведения нескольких чисел или частного двух чисел равна сумме их предельных относительных погрешностей.

Пример 1.3.

Найдите сумму приближенных чисел и = а + Ь + с = 2,72 + + 3,00 + 2,11 при условии, что все значащие цифры данных чисел верные. Определите предельные абсолютную и относительную погрешности этой суммы, а также верные цифры этой суммы.

Решение Очевидно, что и = 7,83 и.

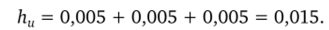
По формуле (1.2) получаем.

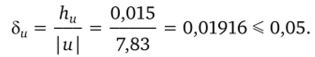
или 8″ = 2%.

Из значения предельной абсолютной погрешности и определения значащей цифры следует, что последняя цифра результата сомнительная и верными являются только первые две цифры.

Пример 1.4.

Найдите произведение приближенных чисел и = abc = 2,72 X X 3,00−2,11 при условии, что все значащие цифры данных чисел верные. Определите предельные относительную и абсолютную погрешности этого произведения, а также его верные цифры.

Решение

Легко вычислить.

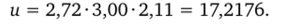
Следуя правилу вычисления относительной погрешности, получаем.

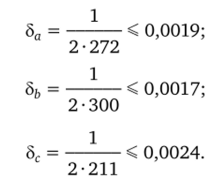
В силу теоремы 1.2 получаем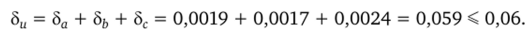

По формуле (1.3) находим абсолютную погрешность:

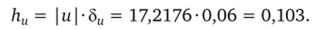
Отсюда следует, что последние четыре цифры результата сомнительные. Итак, верными являются только первые две цифры: и = 17.

Приведенные теоремы позволяют вести строгий учет погрешностей. Например, при сложении 10 чисел, каждое из которых имеет погрешность, не превышающую 0,005, погрешность суммы не превзойдет 0,05. Однако найденная таким образом граница погрешностей обычно бывает значительно завышенной: в большинстве случаев при сложении 10 слагаемых погрешность возрастает не в 10 раз, а лишь немного превышает погрешность слагаемых. Поэтому при выполнении арифметических операций над приближенными числами в тех случаях, когда не требуется строгого учета погрешностей, установлены правила, позволяющие быстро, без громоздких исследований, определить, как нужно проводить вычисления, чтобы получить результат нужной точности. Эти правила не столь точны, как правила вычисления со строгим учетом погрешностей, но для многих вычислений вполне достаточны. Они называются правилами верных цифр. При формулировке этих правил будем считать, что число верных цифр в числах, над которыми производятся арифметические операции, невелико.

Правила верных цифр:

• 1. При сложении и вычитании приближенных чисел в результате младший сохраненный десятичный разряд должен быть тот, который соответствует наименее точному из слагаемых.
• 2. При умножении и делении в результате следует сохранять столько значащих цифр, сколько имеет число с наименьшим числом значащих цифр.
• 3. При возведении в квадрат или куб в результате следует сохранять столько значащих цифр, сколько их имеет возводимое в степень приближенное число.
• 4. При извлечении квадратного или кубического корней в результате следует сохранять столько значащих цифр, сколько их имеет приближенное значение подкоренного числа.
• 5. При вычислениях по данной формуле во всех промежуточных результатах следует сохранять одной цифрой больше, чем рекомендуют предыдущие правила. В окончательном результате эта «запасная» цифра отбрасывается.

6. Если какое-либо используемое в вычислении число имеет больше десятичных знаков (при сложении или вычитании) или больше значащих цифр (при умножении, делении, возведении в степень или извлечении корня), чем другие, то его предварительно следует округлить, сохраняя одну лишнюю цифру.