Индексы дохода и цен

При сравнении потребительских наборов, осуществляемом в рамках теории выявленных предпочтений, используют индексы реального дохода и цен.

Если считать, что расходы потребителя равны его доходам, то для начального (базисного) наблюдения можно записать:

Для второго (текущего) наблюдения можно записать:

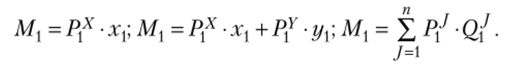
В обоих случаях речь идет о номинальном доходе, т. е. о сумме денег, которую потребитель должен затратить (должен иметь), чтобы купить тот или иной товарный набор. Отнесение номинального дохода (расхода) текущего наблюдения к номинальному доходу (расходу) базисного наблюдения дает нам индекс номинального дохода:

Он показывает изменение стоимости жизни в текущем периоде по сравнению с базисным. В отличие от номинального реальный доход отражает.

вещественное содержание дохода потребителя. Он характеризуется всей массой благ и услуг, которые потребитель может купить на свой денежный (номинальный) доход. Что он конкретно приобретет, зависит от его предпочтений и цен на те или иные товары. В натуральной форме реальный доход (реально покупаемый набор благ) нельзя выразить каким-то одним числом (в штуках, литрах, метрах и т. п.).

Если бы цены всех покупаемых потребителем товаров не изменялись в период между двумя наблюдениями, то индекс номинального дохода отражал бы только изменения физического объема покупаемого набора благ.

Если цены все же меняются, то проблема измерения изменений реального дохода усложняется. Она остается сравнительно простой для случая траты всех денег на покупку только одного товара X. Разделив величину денежного дохода (М) на цену этого товара (Р₀^Л или Р_}^х), можно получить количество покупаемого товара^ (х₀ или х_х). Тогда индекс реального дохода для случаев покупки только одного товара будет равен.

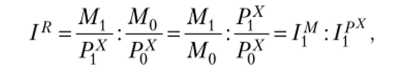
где — индекс номинального дохода; 1(^х — индекс цены товара X в текущем периоде.

Если номинальный доход и цена товара (ов) изменяются в одной пропорции и в одном направлении, то величина реального дохода не меняется, а индекс реального дохода будет равен единице.

В случае покупки более чем одного товара фактор изменения цен при расчете реального дохода можно устранить двумя способами. В одном случае в качестве «весов» можно взять цены базисного периода. Полученный в этом случае индекс реального дохода называется еще индексом объема Ласпейреса:

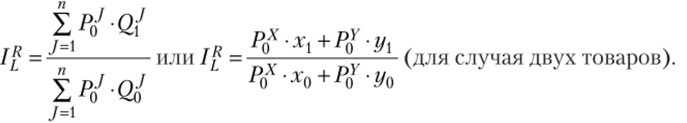
При втором способе расчета индекса реального дохода в качестве «весов» берутся цены текущего периода. Иначе его еще называют индексом объема Паате:

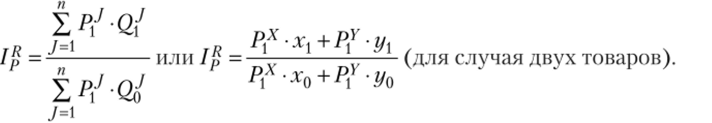
Как можно оценить благосостояние потребителя в текущем периоде по сравнению с базисным? Для ответа на этот вопрос можно использовать теорию выявленных предпочтений.

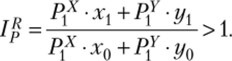
Это равнозначно выражению Р^^х • х₁ 4-• у_х > Р^х • х₀ + Р^ • у₀.

О чем говорит это неравенство? Удовлетворенность (благосостояние) потребителя выше в текущем периоде, поскольку в этом периоде при текущих ценах (Р^х и Pf) он мог бы выбрать набор (д:₀, у₀), но предпочел ему набор (x_v у_х). Если бы индекс Пааше оказался меньше единицы, то мы имели бы неравенство.

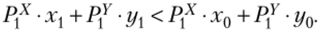
Оно свидетельствует о том, что при новых ценах (ценах текущего периода) набор исходного выбора является недоступным для потребителя. Поэтому говорить о предпочтениях потребителя в этом случае не имеет смысла.

Теперь представим, что индекс реального дохода Ласпейреса меньше единицы.

Тогда.

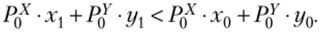
Данное неравенство говорит о том, что набор (х₀, у₀) выявленно предпочитается потребителем набору (x_v у_х). Последний был доступен и при комбинации цен (Р^х и Р₀^У) в базисном периоде, но не был выбран потребителем. И если набор (х_и у_}) был выбран потребителем в текущем периоде, то значит, что более предпочтительный набор (х₀, у₀) перестал быть доступным при новых ценах (Р^х и Pf).

Из этого можно заключить, что уровень благосостояния (удовлетворенности) потребителя оказался выше в базисном периоде, чем в текущем.

Теперь обратимся к индексам цен. Индекс цен — это средневзвешенная величина. В качестве «весов» берутся количества потребленных товаров: базисного периода (индекс цен Ласпейреса) и текущего (индекс цен Пааше):

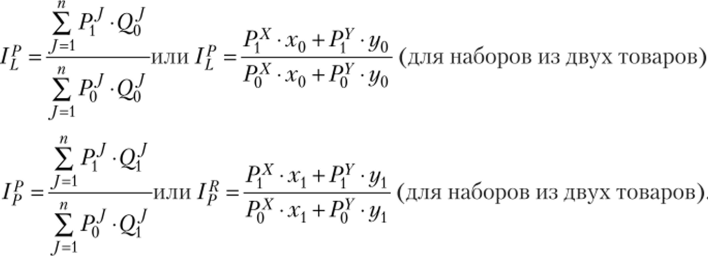
Поскольку в числителях и знаменателях индексов цен находятся цены разных периодов (при одних и тех же наборах), постольку непосредственные сравнения наборов с помощью выявленных предпочтений невозможны.

Тем не менее можно доказать, что если индекс Паате больше индекса номинального дохода, т. е. 1р >7^, то набор, выбранный в базисном году (х₀, г/₀), выявление) предпочитается набору, выбранному в текущем периоде.

Если набор (xj, у_х), выбираемый в текущем периоде, был доступен потребителю и в базисном периоде (т.е. если Р^х • х_{ + PJ? у_х < Р^х • х₀ + Р₀^Г • у₀) и тем не менее в базисном периоде был выбран набор (х₀, г/₀), то это говорит о том, что последний доставляет потребителю большее удовлетворение, т. е. принадлежит к более высокой кривой безразличия. Можно сказать, что набор, выбранный потребителем в базисном периоде (х₀, г/₀), выявленно предпочитается набору, выбранному в текущем периоде (х_1? у_{).

Если обе части последнего неравенства разделить на выражение (Р_{^х • + Pf • у_х), то получим.

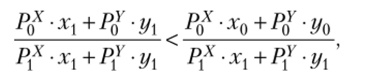
или, что-то же самое:

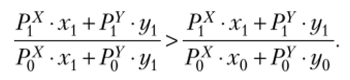
Левая часть выражения — индекс цен Пааше, правая — индекс номинального дохода.

Итак, имеем.

Относительно индекса цен Ласпейреса мы можем доказать, что если он оказывается меньше индекса номинального дохода (/? < 7/^v/), то благосостояние потребителя в результате выбора в текущем году будет выше уровня его удовлетворенности в базисном периоде.

Если, например, известно, что расходы на приобретение выбранного в базисном году набора D (х₀, у₀) в итоге оказываются не больше дохода текущего года (M_t), то это означает, что исходный выбранный набор доступен потребителю и при текущих ценах (Р_х^х и Р*). Если все же потребитель в текущем году выбирает другой оптимальный набор С (х_х, г/j), то это означает, что-либо набор, выбранный в текущем периоде, принадлежит к более высокой кривой безразличия, т. е. несет больше удовлетворения, чем базисный набор D (рис. 28.4): Р_х^х -х₀ н-Р^' • г/₀ <�Р_Х^Х х_{ +Pf у_х, либо оба набора принадлежат одной бюджетной линии, т. е. имеют одинаковую стоимость: ^[1]

Но при этом набор С прямо выявленно предпочитается набору D как принадлежащий к более высокой кривой безразличия.

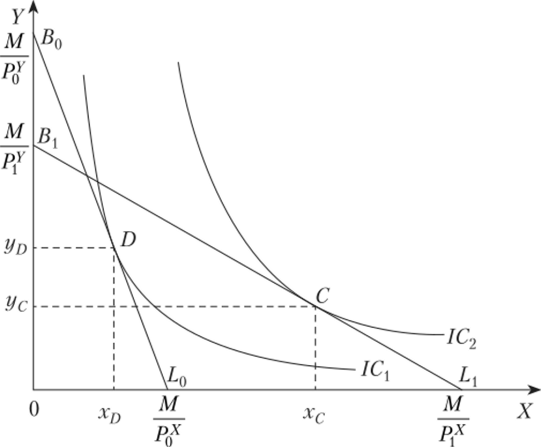
Рис. 28.4. Выявленные предпочтения потребителя в случае, когда индекс цен Ласпейреса меньше индекса номинального дохода

Разделив обе части неравенства.

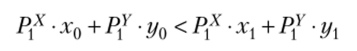
на выражение (Р₀^Х • х₀ + Р₀^У • г/₀), получим.

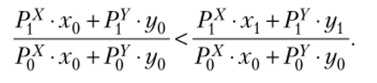
В левой части неравенства имеем индекс цен Ласпейреса, в правой — индекс номинального дохода. Таким образом, мы получили.

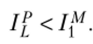
Из анализа индексов цен можно сделать интересный вывод. На самом деле не так важно, больше или меньше единицы окажется индекс цен, гораздо существеннее — будет ли он больше или меньше индекса номинального дохода.

• [1] Если поразмыслить, то нет ничего удивительного в том, что когда рост цен происходитбыстрее роста номинального дохода (/? > /jv/), тогда мы вправе ожидать снижения уровняудовлетворенности потребителя в текущем периоде по сравнению с базисным. А это делаетболее предпочтительный выбор базисного периода недоступным в текущем периоде.